Навигация
Таким образом, «Новые» случаи 23,…, 28 новых возможных решений уравнения (15) не выявили
1. Таким образом, «Новые» случаи 23,…, 28 новых возможных решений уравнения (15) не выявили.
2. Условия 1 и 2 ( продолжения ) Утверждения(1) нами рассмотрены.
*********
Итак, уравнение (15) ![]() , если c и b – взаимно простые целые нечетные числа, имеет решение (после анализа всех полученных решений) только в следующих целых числах:
, если c и b – взаимно простые целые нечетные числа, имеет решение (после анализа всех полученных решений) только в следующих целых числах:
а) ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
б) ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
А это в свою очередь означает, что и рассматриваемое уравнение ![]() (
(![]() ,
,![]() - натуральные числа, где
- натуральные числа, где ![]() при
при ![]() - натуральном) может иметь целые решения либо при
- натуральном) может иметь целые решения либо при ![]() , либо при
, либо при ![]() .
.
************
Вывод: 2-я часть «Утверждения 1» доказана.
В результате исследования уравнения (1) мы имеем:
Вывод 1. Уравнение (1) ![]() (
(![]() ,
,![]() - натуральные числа,
- натуральные числа, ![]() при
при ![]() - натуральном) не имеет решений в отличных от нуля попарно взаимно простых целых числах
- натуральном) не имеет решений в отличных от нуля попарно взаимно простых целых числах ![]() ,
, ![]() и
и ![]() таких, чтобы
таких, чтобы ![]() - было четным,
- было четным, ![]() и
и ![]() - нечетными целыми числами.
- нечетными целыми числами.
Возможны случаи: либо ![]() , либо
, либо ![]() .
.
*******
В качестве подтверждения можно рассмотреть такой пример.
Пример
Нетрудно доказать вышерассмотренным методом, что уравнение ![]() (42), где
(42), где ![]() - натуральное число, a – четное, b и c нечетные целые числа, не имеет решений в отличных от нуля попарно взаимно простых целых числах a, b, c. (Хотя ход доказательства несколько отличается, т.к.
- натуральное число, a – четное, b и c нечетные целые числа, не имеет решений в отличных от нуля попарно взаимно простых целых числах a, b, c. (Хотя ход доказательства несколько отличается, т.к. ![]() =
=![]() = с + b - число четное при q = 2 и b и c нечетных целых числах).
= с + b - число четное при q = 2 и b и c нечетных целых числах).
При ![]() «Исключением» являются
«Исключением» являются ![]() , или
, или ![]() .
.
(При ![]() «Исключением» являются, например,
«Исключением» являются, например, ![]() или
или ![]() , при которых а = 2 и выполняется тождество
, при которых а = 2 и выполняется тождество ![]() (этот случай рассматривать не будем).
(этот случай рассматривать не будем).
Действительно, решениями уравнения, например, a3 = c2 - b2 (43) являются (это хорошо известно в теории чисел) следующие выражения:
a = α2 – δ2 - четное число при α и δ – нечетных или четных.
c = α3 + 3αδ2 - четное число при α и δ – нечетных или четных.
b = 3α2δ + δ3 - четное число при α и δ – нечетных или четных.
(Такой же результат получается (a, c, b – четные числа) для любого уравнения
![]() (42), где
(42), где ![]() - натуральное.)
- натуральное.)
Однако вернемся к уравнению (43) a3 = c2 - b2.
«Исключением» являются следующие его решения:
1. b = ±1; c = ±3; a = 2 (при r = 1 и ![]() = ±3);
= ±3);
2. b = ![]() 3; c = ±1; a = -2 (при r = -1 и
3; c = ±1; a = -2 (при r = -1 и ![]() =
= ![]() 3),
3),
при которых получаем соответственно тождества:
1. 23 ≡ (±3)2 – (±1)2
2. (-2)3 ≡ (±1)2 – (±3)2
**********
Примечание.
1. Великая теорема Ферма для ![]() доказывается аналогичным способом, примененным при доказательстве «Утверждения 1», в результате чего возникает «противоречие» при оценке четности чисел a, b, c. Это мы покажем ниже при доказательстве «Утверждения 2».
доказывается аналогичным способом, примененным при доказательстве «Утверждения 1», в результате чего возникает «противоречие» при оценке четности чисел a, b, c. Это мы покажем ниже при доказательстве «Утверждения 2».
2. Для степени p = 2 в уравнении ![]() такого «противоречия» при оценке четности чисел a, b, c не возникает.
такого «противоречия» при оценке четности чисел a, b, c не возникает.
3. Данное «Утверждение 1» автоматически доказывает справедливость Великой теоремы Ферма для показателя![]() простом, т.к. она является частным случаем этого «Утверждения 1» при
простом, т.к. она является частным случаем этого «Утверждения 1» при ![]() простом. Имея дело с уравнением (44)
простом. Имея дело с уравнением (44) ![]() , где
, где ![]() простое, a, b, c - целые отличные от нуля числа, становится возможным применение метода бесконечного спуска, о чем в свое время упоминалось самим Ферма.
простое, a, b, c - целые отличные от нуля числа, становится возможным применение метода бесконечного спуска, о чем в свое время упоминалось самим Ферма.
«Исключение» (b = ±1 или c = ±1) в «Утверждении 1» на Великую теорему Ферма не распространяется, т.к. в теории чисел хорошо известно, что целые числа a, b, c, удовлетворяющие соотношению (44) (если такие существуют) должны удовлетворять неравенствам | a | > p, | b | > p, | c | > p (Постников М.М. Введение в теорию алгебраических чисел. – М. – Наука. – 1982. - С. 13).
Вывод: Великая теорема Ферма для степени![]() простом доказана.
простом доказана.
********
Утверждение 2,
частным случаем которого является Великая теорема Ферма, для показателя q = 4
Часть 1
Уравнение ![]() (
(![]() - четное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах
- четное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах ![]() ,
, ![]() и
и ![]() таких, чтобы
таких, чтобы ![]() - было четным,
- было четным, ![]() и
и ![]() - нечетными целыми числами.
- нечетными целыми числами.
Часть 2
Случаи (либо b = ± 1, либо c = ± 1) ОТСУТСТВУЮТ.
**********
Часть первая (Утверждения 2)
Уравнение ![]() (
(![]() - четное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах
- четное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах ![]() ,
, ![]() и
и ![]() таких, чтобы
таких, чтобы ![]() - было четным,
- было четным, ![]() и
и ![]() - нечетными целыми числами.
- нечетными целыми числами.
Доказательство
Итак, имеем уравнение ![]() (1), где
(1), где ![]() - четное, числа a, b, c (если, конечно, они существуют) – попарно взаимно простые целые числа (это наше допущение – вопреки «Утверждению 2»), среди которых только одно четное число a.
- четное, числа a, b, c (если, конечно, они существуют) – попарно взаимно простые целые числа (это наше допущение – вопреки «Утверждению 2»), среди которых только одно четное число a.
Из уравнения (1) следует: ![]() =>
=> ![]() (2).
(2).
Пусть ![]() (3), где
(3), где ![]() и β - целые числа, отличные от нуля и c2 + b2 = 2 β (4), где β – нечетное число при c и b- нечетных.
и β - целые числа, отличные от нуля и c2 + b2 = 2 β (4), где β – нечетное число при c и b- нечетных.
*********
Примечание
То, что β в уравнении (4) нечетное число, хорошо известный факт в теории чисел, который легко доказывается.
Представим нечетные числа b и c в виде:
b = 2n1 + 1; c = 2n2 + 1,
где n1 и n2 - произвольные целые числа. Тогда
b2 + c2 = (2n1 + 1)2 + (2n2 + 1)2 = 2 [2 (n12+n22+n1+n2) + 1],
где в квадратных скобках нечетное число, что и требовалось доказать.
*******
Тогда из уравнения (2) следует (с учетом (3) и (4):
![]() =
= ![]() , где c2 + b2 ≠ 0, т.к. c ≠ 0, b ≠ 0, т.е.
, где c2 + b2 ≠ 0, т.к. c ≠ 0, b ≠ 0, т.е.
![]() (5),
(5),
где k – целое число, отличное от нуля, т.к. c и b взаимно простые целые числа (при ![]() – целое число k - четное число, т.к.
– целое число k - четное число, т.к. ![]() пропорционально 4 (явно) при b и с – нечетных числа => 2l-2k – четное число при
пропорционально 4 (явно) при b и с – нечетных числа => 2l-2k – четное число при![]() ).
).
Из соотношений (4) и (5) определяем b2 и c2:
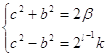 =>
=> 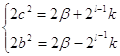 =>
=> 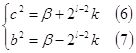
Откуда β = b2 + 2l-2k (8) - нечетное число (из (4)) при b – нечетном и 2l-2k - четном.
*********
Вывод:
1. Из соотношения (4) имеем:
(9) ![]() - нечетное число.
- нечетное число.
2. Из соотношения (5) имеем:
(10) ![]() пропорционально 2 (явно), т.е.
пропорционально 2 (явно), т.е. ![]() - четное число.
- четное число.
Это дополнительная информация о свойствах предполагаемых взаимно простых числах ![]() , которая в дальнейшем нам очень пригодится.
, которая в дальнейшем нам очень пригодится.
*******
Теперь попробуем выразить сумму четвертых степеней чисел c и ![]() . Учитывая соотношения (6) и (7), получим:
. Учитывая соотношения (6) и (7), получим:
 ,
,
![]()
![]() т.е.
т.е. ![]() (11),
(11),
где ![]() - целые числа, которые, в свою очередь, как мы знаем из предыдущего доказательства «Утверждения 1» (для
- целые числа, которые, в свою очередь, как мы знаем из предыдущего доказательства «Утверждения 1» (для ![]() ), могут быть выражены через другие целые числа
), могут быть выражены через другие целые числа ![]() следующим образом:
следующим образом:
(12) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(13) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(14) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(15) ![]() - четное число.
- четное число.
Примечание: во всех последующих исследованиях (Случаях) нас не будут интересовать t =0 и r=0 (при t =0 ![]() и
и ![]() - четные из (12) и (13), при r=0
- четные из (12) и (13), при r=0 ![]() = 0 (из (15)) => а = 0 (из (3)), что противоречит нашему допущению). .
= 0 (из (15)) => а = 0 (из (3)), что противоречит нашему допущению). .
*******
Для простоты опять обозначим правые части уравнений (12), …, (15) буквами С, В, N, К, т.е.
![]() = С
= С
![]() = В
= В
![]() = N
= N
![]() = К,
= К,
и рассмотрим случай, когда в правых частях уравнений (12), …, (15) перед С, В, N, К, стоят «плюсы» и выполняется Условие1.
********
Условие1 (начало)
с2 = С
b2 = B
![]() = N
= N
![]()
Случай «+».
(12+) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(13+) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(14+) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(15+) ![]() - четное число.
- четное число.
Казалось бы, все нормально: четность чисел ![]() в (12+),…, (15+) совпадают при
в (12+),…, (15+) совпадают при ![]() - нечетном с нашими предыдущими рассуждениями.
- нечетном с нашими предыдущими рассуждениями.
Однако не все так просто.
Помимо всего прочего, у нас есть еще две дополнительные информации (9) и (10) (о четности, заключенной в «Выводе» (стр.36)), вытекающие из предположения о том, что, вопреки условию «Утверждения 2», допустим, существуют попарно взаимно простые целые числа ![]() .
.
Попробуем найти сумму ![]() , воспользовавшись их выражениями (12+) и (13+):
, воспользовавшись их выражениями (12+) и (13+):
![]() ,
,
т.е. ![]() => (
=> (![]() ) пропорционально 4, откуда следует, учитывая (9) в «Выводе» (стр.36),
) пропорционально 4, откуда следует, учитывая (9) в «Выводе» (стр.36),
![]() !
!
Т.е., вопреки «Выводу», ![]() является не нечетным, а четным числом, что возможно (из (14)) при
является не нечетным, а четным числом, что возможно (из (14)) при ![]() - четном.
- четном.
Однако, если ![]() - четное, то
- четное, то ![]() (в (12+) и (13+)) являются четными, т.е. в уравнениях (2)
(в (12+) и (13+)) являются четными, т.е. в уравнениях (2) ![]() и (1)
и (1) ![]() числа
числа ![]() - четные, а потому не являются попарно взаимно простыми целыми числами.
- четные, а потому не являются попарно взаимно простыми целыми числами.
Мы пришли к противоречию в Случае «+» с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых ![]() решений.
решений.
********
Вывод. Следовательно, это уравнение (1) ![]() в данном Условии 1 (начало) не имеет решений в целых попарно взаимно простых
в данном Условии 1 (начало) не имеет решений в целых попарно взаимно простых ![]() отличных от нуля числах, где
отличных от нуля числах, где ![]() - четное натуральное число.
- четное натуральное число.
********
Мы рассмотрели случай, когда перед скобками в (12+), …, (15+) стояли «плюсы».
Случай, когда перед теми же скобками стоят «минусы» (Случай «-»), аналогичен вышерассмотренному. Вывод тот же. (Смотри Случай «-» на стр.8.)
********
Примечание
Осталось рассмотреть еще 14 случаев, когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы). Но об этом - во 2-ой части данного Утверждения 2.
********
Т.к. уравнение (11) симметрично для с2 и b2, (для уравнения (11) они равнозначны), то с2 и b2 могут меняться своими выражениями (C и В). Это свойство назовем «новым свойством ![]() ». Поэтому аналогичны вышерассмотренному и случаи («Новые» случаи «+» и «-»), когда опять перед теми же В, С, N и К стоят одинаковые знаки.
». Поэтому аналогичны вышерассмотренному и случаи («Новые» случаи «+» и «-»), когда опять перед теми же В, С, N и К стоят одинаковые знаки.
Условие 2 (начало)
с2 = В
b2 = С
![]() = N
= N
![]()
«Новые» случаи «+» и «-».
(12´±) c2![]() =± В
=± В
(13´±) b2![]() =±С
=±С
(14±) ![]() =± N
=± N
(15±) ![]() =±К.
=±К.
И в этом случае сумма ![]() пропорциональна 4, откуда следует, (учитывая (13) в «Выводе» (стр.36)),
пропорциональна 4, откуда следует, (учитывая (13) в «Выводе» (стр.36)), ![]() !
!
Т.е., вопреки «Выводу», и в этих «Новых» случаях «+» и «-» ![]() является не нечетным, а четным числом, что возможно(из (14±)) при
является не нечетным, а четным числом, что возможно(из (14±)) при ![]() -четном.
-четном.
Однако, если ![]() - четное, то
- четное, то ![]() (в ((12´±) и ((13´±)) являются четными, т.е. в уравнениях (2) и (1) числа
(в ((12´±) и ((13´±)) являются четными, т.е. в уравнениях (2) и (1) числа ![]() - четные, а потому не являются попарно взаимно простыми целыми числами.
- четные, а потому не являются попарно взаимно простыми целыми числами.
Мы пришли к противоречию (в «Новых» случаях «+» и «-») с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых ![]() решений.
решений.
*******
Вывод. Следовательно, это уравнение (1) в данном Условии 2 (начало) не имеет решений в целых попарно взаимно простых ![]() отличных от нуля числах.
отличных от нуля числах.
*******
Примечание
Осталось рассмотреть еще 14 случаев, рассматривающих «новые свойства ![]() », когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы).
», когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы).
Но об этом - во 2-ой части данного Утверждения 2.
********
Уравнение (11![]() ) симметрично и для
) симметрично и для ![]() и для
и для ![]() (для уравнения (11) они равнозначны), которые тоже могут меняться своими выражениями (N и К). Это свойство назовем «похожим свойством
(для уравнения (11) они равнозначны), которые тоже могут меняться своими выражениями (N и К). Это свойство назовем «похожим свойством ![]() и
и ![]() ». А это означает, что нам придется рассмотреть еще 16 «похожих» случаев (с 1-го по 14 и случаи «+» и «-», в которых
». А это означает, что нам придется рассмотреть еще 16 «похожих» случаев (с 1-го по 14 и случаи «+» и «-», в которых ![]() и
и ![]() меняются своими выражениями (N и К)).
меняются своими выражениями (N и К)).
Условие 3.
с2 = С
b2 = B
![]() = К
= К
![]()
« Похожие» случаи «+» и «-».
(12±) c2 = ± (![]() ) = ± С
) = ± С
(13±) b2 = ± (![]() ) = ± В
) = ± В
(14´±) ![]() =
= ![]() = ±К
= ±К
(15´±) ![]()
![]() = ± N
= ± N
Согласно одному из Выводов (формула (10) ![]() пропорционально 2 (явно), при
пропорционально 2 (явно), при ![]() . Но это возможно, глядя на четное (15´±)
. Но это возможно, глядя на четное (15´±) ![]() = ±N= ±(
= ±N= ±(![]() ) только при t- четном, при которых в (12±) и (13±) c и b – четные, чего не должно быть.
) только при t- четном, при которых в (12±) и (13±) c и b – четные, чего не должно быть.
Мы пришли к противоречию (в «Похожих» случаях «+» и «-») с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых ![]() решений.
решений.
*******
В остальных 14 «похожих» случаях, где опять же ![]() = ± N= ± (
= ± N= ± ( ![]() ) и перед С, В, N, К стоят всевозможные знаки (плюсы и минусы), рассуждая аналогичным способом (и при этом не затрагивая «новые свойства
) и перед С, В, N, К стоят всевозможные знаки (плюсы и минусы), рассуждая аналогичным способом (и при этом не затрагивая «новые свойства ![]() » (пояснение (стр.10), подобное для
» (пояснение (стр.10), подобное для ![]() при доказательстве Утверждения 1), мы придем к прежнему результату: c и b – четные, чего не должно быть.
при доказательстве Утверждения 1), мы придем к прежнему результату: c и b – четные, чего не должно быть.
Это значит, что мы опять придем к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых ![]() решений.
решений.
********
Вывод. Следовательно, это уравнение (1) в данном Условии 3 не имеет решений в целых попарно взаимно простых ![]() отличных от нуля числах.
отличных от нуля числах.
*******
Вывод
1. Таким образом, в вышеприведенных Условиях 1 (начало), 2 (начало) и 3 уравнение (1) ![]() (1), где
(1), где ![]() - четное натуральное число, не имеет решений в целых попарно взаимно простых
- четное натуральное число, не имеет решений в целых попарно взаимно простых ![]() отличных от нуля числах.
отличных от нуля числах.
2. 1-я часть «Утверждения 2» (для Условий 1(начало), 2 (начало) и 3) доказана.
*********
Часть вторая (Утверждения 2)
Случаи (либо b = ± 1, либо c = ± 1) ОТСУТСТВУЮТ.
Доказательство
Казалось бы, мы должны рассмотреть еще моменты в Условиях 1 и 2, когда перед скобками в (12), …, (15) стоят разные знаки (как при доказательстве «Утверждения 1» в части 2). Интуиция подсказывает, что эта процедура опять нас приведет к известным значениям b и c: либо ![]() (из
(из ![]() ), либо
), либо ![]() (из
(из ![]() ), либо b и c - четные чего не должно быть, (подобно доказательству части 2 «Утверждения 1»).
), либо b и c - четные чего не должно быть, (подобно доказательству части 2 «Утверждения 1»).
Для подтверждения сказанного рассмотрим подробно только часть Условия 1.
Условие 1 (продолжение).
Случай 1.
![]() (12)
(12)
![]() (13′)
(13′)
![]() (14)
(14)
![]() (15) ,
(15) ,
которые также являются решениями уравнения (11)
![]() .
.
Тогда сумма ![]() имеет вид:
имеет вид:
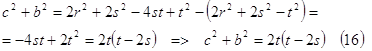
Учитывая (10) и (15), можно получить разность ![]() :
:
![]()
![]()
![]() =>
=> ![]() .
.
Выразим из (17) и (16) ![]() :
:
![]() =>
=> ![]()
![]() =>
=> ![]() .
.
По условию ![]() должны быть взаимно простыми целыми числами, поэтому их общий множитель
должны быть взаимно простыми целыми числами, поэтому их общий множитель ![]() .
.
Т.о., ![]() имеют вид:
имеют вид:
![]() ,
, ![]() , а их сумма
, а их сумма ![]() .
.
Т.к. из (4) c2 + b2 = 2 β, то ![]() =>
=> ![]() .
.
Из (15) с учетом (20) выразим ![]() :
:
![]() , т.е.
, т.е. ![]() .
.
Т.о., ![]() ,
, ![]() , т.е.
, т.е.
![]()
![]() ,
,
выражения которых, с учетом (24), полностью совпадают с (6) и (7), т.е. с уравнениями
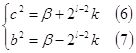
Теперь, с учетом (13′) и (14), найдем сумму ![]() :
:
![]() т.к.
т.к. ![]() , т.е.
, т.е. ![]() .
.
(Здесь чередование «плюса» и «минуса» такое же, как и у единицы в (20). В последующих действиях мы это учтем).
Теперь, учитывая (23), получим значение для b2:
![]() , т.к. из (20) получается
, т.к. из (20) получается
![]() (20′).
(20′).
Итак, ![]() (28), что для целых чисел неприемлемо.
(28), что для целых чисел неприемлемо.
Этот случай нас не интересует.
********
Тем не менее продолжим, т.к. результат, который мы получим, в дальнейшем нам пригодится.
Учитывая (26), получим
![]() =>
=> ![]() .
.
Теперь, с учетом (29), можно получить окончательное выражение для с 2 (из (25)):
![]() , т.е.
, т.е. ![]() .
.
Таким образом, уравнение ![]() (11), решениями которого являются (12), (13′) , (14), (15), в конечном счете имеет следующие решения:
(11), решениями которого являются (12), (13′) , (14), (15), в конечном счете имеет следующие решения:
![]() ,
, ![]() ,
,
![]() (28),
(28), ![]() ,
,
где ![]() - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
*******
Случай 2
Нетрудно догадаться, что если бы у уравнения (11) были бы решения, противоположные по знаку с решениями (12), (13′) , (14), (15), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (30), (28), (29) и (24), т.е.
![]() (30´), => c =
(30´), => c = ![]() (30´),
(30´), ![]() (29´)
(29´)
![]() (28´), => b =
(28´), => b = ![]() 1 (28´),
1 (28´), ![]() (24´), где
(24´), где
![]() - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
Случай 3
![]() (12)
(12)
![]() (13′)
(13′)
![]() (14)
(14)
![]() (15′) ,
(15′) ,
которые также являются решениями уравнения
![]() (11).
(11).
Тогда сумма ![]() имеет вид:
имеет вид:
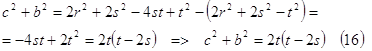
Учитывая (10) и (15), можно получить разность ![]() :
:
![]()
![]() -
-![]() =>
=> ![]() .
.
Выразим из (31) и (16) ![]() :
:
![]() =>
=> ![]() (32)
(32)
![]() =>
=> ![]() (33).
(33).
По условию ![]() должны быть взаимно простыми целыми нечетными числами, поэтому их общий множитель
должны быть взаимно простыми целыми нечетными числами, поэтому их общий множитель ![]() .
.
Т.о., ![]() имеют вид:
имеют вид:
![]() (34),
(34), ![]() (35), а их сумма
(35), а их сумма ![]() .
.
Т.к. из (4) c2 + b2 = 2 β, то ![]() и
и ![]() .
.
Из (15´) с учетом (20) выразим ![]() :
:
![]() , т.е.
, т.е. ![]() (24´).
(24´).
Т.о., ![]() ,
, ![]() ,
,
где![]() , т.е.
, т.е.
![]() ,
,
![]() ,
,
выражения которых, с учетом (24´), полностью совпадают с (6) и (7), т. е. с уравнениями
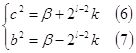
Теперь, с учетом (13′) и (14), найдем сумму ![]() :
:
![]()
т.к. ![]() , т.е.
, т.е. ![]() .
.
(Здесь чередование «плюса» и «минуса» такое же, как и у единицы в (20). В последующих действиях мы это учтем.)
Теперь, учитывая (23), получим значение для b2:
![]() ,т.к. из (20) получается
,т.к. из (20) получается
![]() .
.
Итак, ![]() (28), что для целых чисел неприемлемо.
(28), что для целых чисел неприемлемо.
Этот случай нас не интересует.
*******
Тем не менее продолжим, т.к. результат, который мы получим, в дальнейшем нам пригодится.
Учитывая (26´), получим ![]() =>
=> ![]() (29´´).
(29´´).
Теперь, с учетом (29´´), можно получить окончательное выражение для с 2 (из (25´)):
![]() , т.е.
, т.е. ![]() (30´´).
(30´´).
Таким образом, уравнение ![]() (11), решениями которого являются (12), (13′), (14) и (15´), в конечном счете имеет следующие решения:
(11), решениями которого являются (12), (13′), (14) и (15´), в конечном счете имеет следующие решения:
![]() (30´´),
(30´´), ![]() ,
,
![]() (28),
(28), ![]() (24´),
(24´),
где ![]() - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
***********
Случай 4
Нетрудно догадаться, что если бы у уравнения (11) были бы решения, противоположные по знаку с решениями (12), (13′), (14) и (15´), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (30´´), (28), (29´´) и (24´), т.е.
![]() (30´´´), =>
(30´´´), => ![]() (30´´´),
(30´´´), ![]() (29´´´),
(29´´´), ![]() (28´), => b =
(28´), => b = ![]() (28´),
(28´), ![]() (24),
(24),
где ![]() - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
*******
Подведем некоторый итог. Нами рассмотрено 4 случая решений уравнения (11).
Обозначим снова следующие выражения буквами С, В, N, К:
![]() = С
= С
![]() = В
= В
![]() = N
= N
![]() = К.
= К.
Тогда эти первые 4 случая следующие:
1. (12) ![]() 2. (12´)
2. (12´) ![]() (30´)
(30´)
(13´) ![]() (28) (13)
(28) (13) ![]() (28´)
(28´)
(14) ![]() (29) (14´)
(29) (14´) ![]() (29´)
(29´)
(15) ![]() (24) (15´)
(24) (15´) ![]() (24´)
(24´)
3. (12) ![]() (30´´) 4. (12´)
(30´´) 4. (12´) ![]() (30´´´)
(30´´´)
(13´) ![]() (28) (13)
(28) (13) ![]() (28´)
(28´)
(14) ![]() (29´´) (14´)
(29´´) (14´) ![]() (29´´´)
(29´´´)
(15´) ![]() (24´) (15)
(24´) (15) ![]() (24).
(24).
Рассмотрим еще 4 случая.
5. с2 = С 6. с2 = - С 7. c2 = C 8. c2 = -C
b2 = - B b2 = B b2 = - B b2 = B
![]() = - N
= - N ![]() = N
= N ![]() = - N
= - N ![]() = N
= N
![]()
![]()
![]()
![]()
*******
Итак, рассмотрим случай 5.
Случай 5.
![]() (12),
(12),
![]() (13´),
(13´),
![]() (14´),
(14´),
![]() (15) , которые также являются решениями уравнения
(15) , которые также являются решениями уравнения
![]() (11)
(11)
Но данный случай аналогичен случаю 5 «Части 2» «Утверждения 1», где получены следующие решения уравнения (15):
![]() (41),
(41), ![]() , где
, где ![]() - взаимно простые нечетные целые
- взаимно простые нечетные целые ![]() (40),
(40), ![]() (38´), числа.
(38´), числа.
Следовательно, в данном рассматриваемом Случае 5 у уравнения (11) следующие решения:
![]() (32) => b
(32) => b![]() (32),
(32), ![]() (24)
(24)
![]() (31) => с =
(31) => с = ![]() (31),
(31), ![]() (29´) ,
(29´) ,
где ![]() взаимно простые целые нечетные числа.
взаимно простые целые нечетные числа.
*******
Случай 6
Нетрудно догадаться, что если бы у уравнения (11) были решения, противоположные по знаку с решениями (12), (13′), (14´) и (15), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (32), (31), (29´) и (24), т.е.
![]() (31´),
(31´), ![]() (29),
(29),
![]() (32´),
(32´), ![]() (24´), где
(24´), где ![]() - взаимно простые целые нечетные числа.
- взаимно простые целые нечетные числа.
Но этот случай нас не интересует, т.к. с не является целым числом.
*******
Случай 7
![]() (12),
(12),
![]() (13´),
(13´),
![]() (14´),
(14´),
![]() (15´), которые также являются решениями уравнения
(15´), которые также являются решениями уравнения
![]() (11).
(11).
Но данный случай аналогичен случаю 7 «Части 2» «Утверждения 1», где получены следующие решения уравнения (15):
![]() (40),
(40), ![]() (38´´´),
(38´´´),
![]() (41´´),
(41´´), ![]() (33´),
(33´),
где ![]() - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
Следовательно, в данном рассматриваемом случае 7 у уравнения (11) следующие решения:
![]() (31) => с =
(31) => с = ![]() (31),
(31), ![]() (29´´´) ,
(29´´´) ,
![]() (32´) => b
(32´) => b![]() (32´´),
(32´´), ![]() (24´),
(24´),
где ![]() - взаимно простые целые нечетные числа.
- взаимно простые целые нечетные числа.
*******
Случай 8
Нетрудно догадаться, что если бы у уравнения (11) были решения, противоположные по знаку с решениями (12), (13′), (14´) и (15´), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (32´´), (31), (29´´´) и (24´), т.е.
![]() (31´),
(31´), ![]() (29´´),
(29´´),
![]()
![]() ,
, ![]() (24), где
(24), где ![]() - взаимно простые целые нечетные числа.
- взаимно простые целые нечетные числа.
Но этот случай нас не интересует, т.к. с не является целым числом.
********
Вывод
Итак, после анализа полученных решений в Случаях 1, …,8, уравнение (11) ![]() , где c и b – взаимно простые целые нечетные числа, имеет решения в следующих целых числах:
, где c и b – взаимно простые целые нечетные числа, имеет решения в следующих целых числах:
а) ![]() ; b
; b![]() ;
; ![]() ;
; ![]() ;
;
б) ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
********
Таким образом, само исследование решений уравнения (11) в случаях 1, …, 8 при доказательстве Утверждения 2 и его результат, полностью совпадают с исследованием решений уравнения (15) (в аналогичных случаях при доказательстве Утверждения 1) и с его результатом.
Действительно, вот, например, результаты исследований уравнения (15) в первых 4-х случаях Условия 1(Утверждение 1, Часть 2):
1. (16) ![]() 2. (16´)
2. (16´) ![]() (39´)
(39´)
(17´) ![]() (37) (17)
(37) (17) ![]() (37´)
(37´)
(18) ![]() (18´)
(18´) ![]() (38´)
(38´)
(19) ![]() (33) (19´)
(33) (19´) ![]() (33´)
(33´)
3. (16) ![]() (39´´) 4. (16´)
(39´´) 4. (16´) ![]() (39´´´)
(39´´´)
(17´) ![]() (37) (17)
(37) (17) ![]() (37´)
(37´)
(18) ![]() (38´´) (18´)
(38´´) (18´) ![]() (38´´´)
(38´´´)
(19´) ![]() (33´) (19)
(33´) (19) ![]() (33).
(33).
А вот результаты исследований уравнения (11) в первых 4-х случаях Условия 1 (Утверждение 2,Часть 2):
1. (12) ![]() 2. (12´)
2. (12´) ![]() (30´)
(30´)
(13´) ![]() (28) (13)
(28) (13) ![]() (28´)
(28´)
(14) ![]() (29) (14´)
(29) (14´) ![]() (29´)
(29´)
(15) ![]() (24) (15´)
(24) (15´) ![]() (24´)
(24´)
3. (12) ![]() (30´´) 4. (12´)
(30´´) 4. (12´) ![]() (30´´´)
(30´´´)
(13´) ![]() (28) (13)
(28) (13) ![]() (28´)
(28´)
(14) ![]() (29´´) (14´)
(29´´) (14´) ![]() (29´´´)
(29´´´)
(15´) ![]() (24´) (15)
(24´) (15) ![]() (24).
(24).
Наблюдается полное совпадение результатов (здесь подразумевается, что решения уравнения (15) c и b в верхних 4-х случаях соответствуют решениям уравнения (11)
с2 и b2 в нижних 4-х случаях). То же самое совпадение результатов наблюдается и в следующих за ними 4-х случаях.
********
Поэтому нетрудно понять, что остальные результаты исследований случаев с 9-го по 28-й в данном доказательстве Утверждения 2 (подобные вышерассмотренным случаям 9, …, 28 при доказательстве Утверждения 1) тоже совпадут и никаких новых решений нам не дадут, кроме как:
либо ![]() , либо
, либо ![]() , либо c и b не являются целыми числами, либо c и b – четные числа, чего не должно быть.
, либо c и b не являются целыми числами, либо c и b – четные числа, чего не должно быть.
********
Из этого набора решений уравнения (11) нас, естественно, интересуют только те, которые могут являться решениями уравнения (1) ![]() (1), где
(1), где ![]() - четное натуральное число, т.е. либо
- четное натуральное число, т.е. либо ![]() , либо
, либо ![]() .
.
*******
Но в теории чисел хорошо известно (Постников М.М. Введение в теорию алгебраических чисел. – М .- Наука. – 1982. - С. 13), что для четных степеней уравнения ![]() (где
(где ![]() , q=2 q
, q=2 q![]() ) - показатели четные при
) - показатели четные при ![]() ≠ 0 и q
≠ 0 и q![]() ≠ 0 - натуральных, в уравнении
≠ 0 - натуральных, в уравнении ![]() целочисленные его решения (если они существуют) должны удовлетворять неравенствам:
целочисленные его решения (если они существуют) должны удовлетворять неравенствам:
|![]() | > 2, |
| > 2, | ![]() | > 2, | c
| > 2, | c![]() | > 2 => |a| > 1, | b | > 1, |c| > 1,
| > 2 => |a| > 1, | b | > 1, |c| > 1,
т.е. в уравнении a2+ b4 = c4b ![]() и c
и c ![]() => в уравнении
=> в уравнении ![]() (1) при
(1) при ![]() - четном числе b
- четном числе b![]() и c
и c![]() ,
,
т.е. случаи (либо b = ± 1, либо c = ± 1) ОТСУТСТВУЮТ.
********
Вывод: 2-я часть «Утверждения 2» доказана.
*******
В результате исследования уравнения (1) мы имеем:
Вывод:
1. Уравнение (1) ![]() , где
, где ![]() ≥2 - четное не имеет решений в попарно простых целых числах a, b, и c таких, чтобы
≥2 - четное не имеет решений в попарно простых целых числах a, b, и c таких, чтобы ![]() - было четным,
- было четным, ![]() и
и ![]() - нечетными целыми числами.
- нечетными целыми числами.
2. «Утверждение 2» нами полностью доказано.
*******
Примечание
1. Понятно, что приведенное доказательство «Утверждения 2» для q = 4 = 2m, где m = 2, распространяется и на показатель степени q=2m при m>2 – натуральном.
2. Если уравнение al+ b4 = c4, где![]() ≥2 - четное, неразрешимо в попарно простых целых числах a, b, и c, то и уравнение a4+ b4 = c4не только неразрешимо в этих же числах, но и вообще неразрешимо ни в каких других целых числах (не являющихся попарно взаимно простыми целыми числами).
≥2 - четное, неразрешимо в попарно простых целых числах a, b, и c, то и уравнение a4+ b4 = c4не только неразрешимо в этих же числах, но и вообще неразрешимо ни в каких других целых числах (не являющихся попарно взаимно простыми целыми числами).
Вывод : Великая теорема Ферма для показателя l= q= 4 доказана.
3. Результат доказательства, а именно четность чисел a, b, c в уравнении al+ b4 = c4 (![]() ≥2 - четное), а, следовательно, в уравнении a4+ b4 = c4 дает возможность в этом уравнении применить метод бесконечного спуска, о чем в свое время не только упоминалось самим Ферма, но и им использовалось.
≥2 - четное), а, следовательно, в уравнении a4+ b4 = c4 дает возможность в этом уравнении применить метод бесконечного спуска, о чем в свое время не только упоминалось самим Ферма, но и им использовалось.
На основании Выводов о Великой теореме Ферма (стр.34, стр.49) получаем окончательный вывод.
Окончательный «Вывод»: Великая теорема Ферма доказана.
********
Утверждение 3
Часть 1
Уравнение ![]() (
(![]() ≥ 3 – нечетное натуральное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах
≥ 3 – нечетное натуральное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах ![]() ,
, ![]() и
и ![]() таких, чтобы
таких, чтобы ![]() - было четным,
- было четным, ![]() и
и ![]() - нечетными целыми числами.
- нечетными целыми числами.
Часть 2
Возможны случаи: либо b = ± 1, либо c = ± 1.
*********
Часть первая (Утверждения 3)
Уравнение ![]() (
(![]() ≥ 3 – нечетное натуральное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах
≥ 3 – нечетное натуральное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах ![]() ,
, ![]() и
и ![]() таких, чтобы
таких, чтобы ![]() - было четным,
- было четным, ![]() и
и ![]() - нечетными целыми числами.
- нечетными целыми числами.
Доказательство
Первая часть доказательства «Утверждения 3» аналогична «Части первой» доказательства «Утверждения 2».
Итак, имеем уравнение ![]() (1), где
(1), где ![]() ≥ 3 – нечетное натуральное, числа a, b, c (если, конечно, они существуют) – попарно взаимно простые целые числа (это наше допущение – вопреки «Утверждению 3»), среди которых только одно четное число a.
≥ 3 – нечетное натуральное, числа a, b, c (если, конечно, они существуют) – попарно взаимно простые целые числа (это наше допущение – вопреки «Утверждению 3»), среди которых только одно четное число a.
Из уравнения (1) следует:
![]() =>
=> ![]() (2).
(2).
Пусть ![]() (3), где
(3), где ![]() и β - целые числа, отличные от нуля и c2 + b2 = 2 β (4), где β – нечетное число при с и b – нечетных.
и β - целые числа, отличные от нуля и c2 + b2 = 2 β (4), где β – нечетное число при с и b – нечетных.
******
Примечание
То, что β в уравнении (4) нечетное число, хорошо известный факт в теории чисел, который мы ранее уже учитывали («Примечание», стр. 35).
Представим нечетные числа b и c в виде:
b = 2n1 + 1; c = 2n2 + 1, где n1 и n2 - произвольные целые числа. Тогда
b2 + c2 = (2n1 + 1)2 + (2n2 + 1)2 = 2 [2 (n12+n22+n1+n2) + 1],
где в квадратных скобках нечетное число, что и требовалось доказать
*******
Тогда из уравнения (2) следует (с учетом (3) и (4)):
![]() =
= ![]() , где c2 + b2 ≠ 0, т.к. c ≠ 0, b ≠ 0, т.е.
, где c2 + b2 ≠ 0, т.к. c ≠ 0, b ≠ 0, т.е.
![]() (5),
(5),
где k – целое число, отличное от нуля, т.к. c и b взаимно простые целые числа.
Из соотношений (4) и (5) определяем b2 и c2:
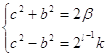 =>
=> 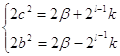 =>
=> 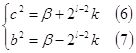
Откуда β = b2 + 2l-2k (8) - нечетное число (из (4)) при b – нечетном и 2l-2k - четном, т.к. ![]() ≥ 3 – нечетное натуральное число.
≥ 3 – нечетное натуральное число.
Вывод:
1. Из соотношения (4) имеем:
(9) ![]() - нечетное число.
- нечетное число.
2. Из соотношения (5) имеем:
(10) ![]() пропорционально 2 (явно), т.е.
пропорционально 2 (явно), т.е. ![]() - четное число.
- четное число.
Это дополнительная информация о свойствах предполагаемых взаимно простых числах ![]() , которая в дальнейшем нам очень пригодится.
, которая в дальнейшем нам очень пригодится.
*******
Теперь попробуем выразить сумму четвертых степеней чисел c и ![]() . Учитывая соотношения (6) и (7), получим:
. Учитывая соотношения (6) и (7), получим:
![]()
![]()
 ,
,
т.е. ![]() (11),
(11),
где ![]() - целые числа, которые, в свою очередь, как мы знаем из предыдущего доказательства «Утверждения 1» (для
- целые числа, которые, в свою очередь, как мы знаем из предыдущего доказательства «Утверждения 1» (для ![]() ), могут быть выражены через другие целые числа
), могут быть выражены через другие целые числа ![]() следующим образом:
следующим образом:
(12) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(13) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(14) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(15) ![]() - четное число.
- четное число.
Примечание: во всех последующих исследованиях (Случаях) нас не будут интересовать t =0 и r=0 (при t =0 ![]() и
и ![]() - четные из (12) и (13), при r=0
- четные из (12) и (13), при r=0 ![]() = 0 (из (15)) => а = 0 (из (3)), что противоречит нашему допущению).
= 0 (из (15)) => а = 0 (из (3)), что противоречит нашему допущению).
Для простоты опять (как в утверждениях 1 и 2) обозначим правые части уравнений (12), …, (15) буквами С, В, N, К, т.е.
![]() = С
= С
![]() = В
= В
![]() = N
= N
![]() = К ,
= К ,
и рассмотрим случай, когда в правых частях уравнений (12), …, (15) перед С, В, N, К, стоят «плюсы» и выполняется Условие1.
Условие1 (начало).
с2 = С
b2 = B
![]() = N
= N
![]()
Случай «+».
(12+) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(13+) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(14+) ![]() - нечетное число при
- нечетное число при ![]() - нечетном;
- нечетном;
(15+) ![]() - четное число.
- четное число.
Казалось бы, все нормально: четность чисел ![]() в (12+), …, (15+) совпадают при
в (12+), …, (15+) совпадают при ![]() -нечетном с нашими предыдущими рассуждениями.
-нечетном с нашими предыдущими рассуждениями.
Однако не все так просто.
Помимо всего прочего, у нас есть еще две дополнительные информации (9) и (10) (о четности, заключенной в «Выводе» (стр.36)), вытекающие из предположения о том, что, вопреки условию «Утверждения 2», допустим, существуют попарно взаимно простые целые числа ![]() .
.
Попробуем найти сумму ![]() , воспользовавшись их выражениями (12+) и (13+):
, воспользовавшись их выражениями (12+) и (13+):
![]() ,
,
т.е. ![]() => (
=> (![]() ) пропорционально 4, откуда следует, учитывая (9) в «Выводе» (стр.36),
) пропорционально 4, откуда следует, учитывая (9) в «Выводе» (стр.36),
![]() !
!
Т.е., вопреки «Выводу», ![]() является не нечетным, а четным числом, что возможно (из (14)) при
является не нечетным, а четным числом, что возможно (из (14)) при ![]() -четном.
-четном.
Однако, если ![]() - четное, то
- четное, то ![]() (в (12+) и (13+)) являются четными, т.е. в уравнениях (2)
(в (12+) и (13+)) являются четными, т.е. в уравнениях (2) ![]() и (1)
и (1) ![]() числа
числа ![]() - четные, а потому не являются попарно взаимно простыми целыми числами.
- четные, а потому не являются попарно взаимно простыми целыми числами.
Мы пришли к противоречию в Случае «+» с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых ![]() решений.
решений.
*******
Вывод. Следовательно, это уравнение (1) ![]() в данном Условии 1(начало) не имеет решений в целых попарно взаимно простых
в данном Условии 1(начало) не имеет решений в целых попарно взаимно простых ![]() отличных от нуля числах, где
отличных от нуля числах, где ![]() - нечетное натуральное число.
- нечетное натуральное число.
********
Мы рассмотрели случай, когда перед скобками в (12+), …, (15+) стояли «плюсы».
Случай, когда перед теми же скобками стоят «минусы» (Случай «-»), аналогичен вышерассмотренному. Вывод тот же. (Смотри Случай «-» на стр.8.)
*********
Примечание
Осталось рассмотреть еще 14 случаев, когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы). Но об этом - во 2-ой части данного Утверждения 3.
********
Т.к. уравнение (11) симметрично для с2 и b2, (для уравнения 11 они равнозначны), то с2 и b2 могут меняться своими выражениями (C и В). Это свойство назовем «новым свойством ![]() ». Поэтому аналогичны вышерассмотренному и случаи («Новые» случаи «+» и «-»), когда опять же перед теми же скобками стоят одинаковые знаки.
». Поэтому аналогичны вышерассмотренному и случаи («Новые» случаи «+» и «-»), когда опять же перед теми же скобками стоят одинаковые знаки.
Условие 2 (начало).
с2 = В
b2 = С
![]() = N
= N
![]()
«Новые» случаи «+» и «-».
(12´±) c2![]() =± В
=± В
(13´±) b2![]() =±С
=±С
(14±) ![]() =± N
=± N
(15±) ![]() =±К.
=±К.
И в этом случае сумма ![]() пропорциональна 4, откуда следует, (учитывая (13) в «Выводе» (стр.36)),
пропорциональна 4, откуда следует, (учитывая (13) в «Выводе» (стр.36)), ![]() !
!
Т.е., вопреки «Выводу», и в этих «Новых» случаях «+» и «-» ![]() является не нечетным, а четным числом, что возможно(из (14±)) при
является не нечетным, а четным числом, что возможно(из (14±)) при ![]() -четном.
-четном.
Однако, если ![]() - четное, то
- четное, то ![]() (в ((12´±) и ((13´±)) являются четными, т.е. в уравнениях (2) и (1) числа
(в ((12´±) и ((13´±)) являются четными, т.е. в уравнениях (2) и (1) числа ![]() - четные, а потому не являются попарно взаимно простыми целыми числами.
- четные, а потому не являются попарно взаимно простыми целыми числами.
Мы пришли к противоречию (в «Новых» случаях «+» и «-») с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых ![]() решений.
решений.
********
Вывод. Следовательно, это уравнение (1) в данном Условии 2 (начало) не имеет решений в целых попарно взаимно простых ![]() отличных от нуля числах.
отличных от нуля числах.
*******
Примечание
Осталось исследовать еще 14 случаев, рассматривающих «новые свойства ![]() », когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы).
», когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы).
Но об этом во 2-ой части данного Утверждения 3.
********
Уравнение (11) симметрично и для ![]() и для
и для ![]() (для уравнения (11) они равнозначны), которые тоже могут меняться своими выражениями (N и К). Это свойство назовем «похожим свойством
(для уравнения (11) они равнозначны), которые тоже могут меняться своими выражениями (N и К). Это свойство назовем «похожим свойством ![]() и
и ![]() ». А это означает, что нам придется рассмотреть еще 16 «похожих» случаев (с 1-го по 14 и случаи «+» и «-», в которых
». А это означает, что нам придется рассмотреть еще 16 «похожих» случаев (с 1-го по 14 и случаи «+» и «-», в которых ![]() и
и ![]() меняются своими выражениями (N и К)).
меняются своими выражениями (N и К)).
Условие 3.
с2 = С
b2 = B
![]() = К
= К
![]()
«Похожие» случаи «+» и «-».
(12±) c2 = ± (![]() ) = ± С
) = ± С
(13±) b2 = ± (![]() ) = ± В
) = ± В
(14´±) ![]() =
= ![]() = ±К
= ±К
(15´±) ![]()
![]() = ± N.
= ± N.
Согласно одному из Выводов (формула (10) ![]() пропорционально 2 (явно), при
пропорционально 2 (явно), при ![]() . Но это возможно, глядя на четное (15´±)
. Но это возможно, глядя на четное (15´±) ![]() = ±N= ±(
= ±N= ±(![]() ) только при t-четном, при которых в (12±) и (13±) c и b – четные, чего не должно быть.
) только при t-четном, при которых в (12±) и (13±) c и b – четные, чего не должно быть.
Мы пришли к противоречию (в «Похожих» случаях «+» и «-») с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых ![]() решений.
решений.
*******
В остальных 14 «похожих» случаях, где опять же ![]() = ± N= ± (
= ± N= ± ( ![]() ) и перед С, В, N, К стоят всевозможные знаки (плюсы и минусы), рассуждая аналогичным способом (и при этом не затрагивая «новые свойства
) и перед С, В, N, К стоят всевозможные знаки (плюсы и минусы), рассуждая аналогичным способом (и при этом не затрагивая «новые свойства ![]() » (пояснение (стр.10), подобное для
» (пояснение (стр.10), подобное для ![]() проведено при доказательстве Утверждения 1), мы придем к прежнему результату: c и b – четные, чего не должно быть.
проведено при доказательстве Утверждения 1), мы придем к прежнему результату: c и b – четные, чего не должно быть.
Это значит, что мы опять придем к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых ![]() решений.
решений.
********
Вывод. Следовательно, это уравнение (1) в данном Условии 3 не имеет решений в целых попарно взаимно простых ![]() отличных от нуля числах.
отличных от нуля числах.
*******
Вывод
1. Таким образом, в вышерассмотренных Условиях 1 (начало), 2 (начало) и 3 уравнение (1) ![]() (1), где
(1), где ![]() ≥ 3 – нечетное натуральное число, не имеет решений в целых попарно взаимно простых
≥ 3 – нечетное натуральное число, не имеет решений в целых попарно взаимно простых ![]() отличных от нуля числах.
отличных от нуля числах.
2. 1-я часть «Утверждения3» (для Условий 1 (начало), 2 (начало) и 3) доказана.
*********
Часть вторая (Утверждения3)
Возможны случаи: либо ![]() , либо
, либо ![]() .
.
(Об «Исключении» из общего правила)
Доказательство
Казалось бы, мы должны рассмотреть еще моменты в Условиях 1 и 2, когда перед скобками в (12), …, (15) стоят разные знаки (как при доказательстве «Утверждения 2» в части 2). Интуиция подсказывает, что эта процедура опять нас приведет к известным значениям b и c: либо ![]() (из
(из ![]() ), либо
), либо ![]() (из
(из ![]() ), либо b и c – четные, чего не должно быть, либо b и c не являются целыми числами (подобно доказательству части 2 «Утверждения 2»).
), либо b и c – четные, чего не должно быть, либо b и c не являются целыми числами (подобно доказательству части 2 «Утверждения 2»).
Для подтверждения сказанного рассмотрим подробно только часть Условия 1.
Итак, осталось рассмотреть случаи, когда перед скобками стоят разные знаки.
Случай 1.
![]() (12)
(12)
![]() (13′)
(13′)
![]() (14)
(14)
![]() (15) , которые также являются решениями уравнения
(15) , которые также являются решениями уравнения
(11) ![]() .
.
Тогда сумма ![]() имеет вид:
имеет вид:
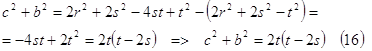
Учитывая (10) и (15), можно получить разность ![]() :
:
![]()
![]()
![]() =>
=> ![]() .
.
Выразим из (17) и (16) ![]() :
:
![]() =>
=> ![]()
![]() =>
=> ![]() .
.
По условию ![]() должны быть взаимно простыми целыми числами, поэтому их общий множитель
должны быть взаимно простыми целыми числами, поэтому их общий множитель ![]() .
.
Т.о., ![]() имеют вид:
имеют вид:
![]() ,
, ![]() , а их сумма
, а их сумма ![]() .
.
Т.к. из (4) c2 + b2 = 2 β, то ![]() =>
=> ![]() .
.
Из (15) с учетом (20) выразим ![]() :
:
![]() , т.е.
, т.е. ![]() .
.
Т.о., ![]() ,
, ![]() , т.е.
, т.е.
![]()
![]() ,
,
выражения которых, с учетом (24), полностью совпадают с (6) и (7), т.е. с уравнениями
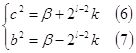
Теперь, с учетом (13′) и (14), найдем сумму ![]() :
:
![]() т.к.
т.к. ![]() , т.е.
, т.е. ![]() .
.
(Здесь чередование «плюса» и «минуса» такое же, как и у единицы в (20). В последующих действиях мы это учтем.)
Теперь, учитывая (23), получим значение для b2:
![]() , т.к. из (20) получается
, т.к. из (20) получается
![]() (20′).
(20′).
Итак, ![]() (28), что для целых чисел неприемлемо.
(28), что для целых чисел неприемлемо.
Этот случай нас не интересует.
********
Тем не менее продолжим, т.к. результат, который мы получим, в дальнейшем нам пригодится.
Учитывая (26), получим ![]() =>
=> ![]() .
.
Теперь, с учетом (29), можно получить окончательное выражение для с 2 (из (25)):
![]() , т.е.
, т.е. ![]() .
.
Таким образом, уравнение ![]() (11), решениями которого являются (12), (13′) , (14), (15), в конечном счете имеет следующие решения:
(11), решениями которого являются (12), (13′) , (14), (15), в конечном счете имеет следующие решения:
![]() ,
, ![]() ,
,
![]() (28),
(28), ![]() ,
,
где ![]() - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
*******
Случай 2
Нетрудно догадаться, что если бы у уравнения (11) были бы решения, противоположные по знаку с решениями (12), (13′) , (14), (15), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (30), (28), (29) и (24), т.е.
![]() (30´), => c =
(30´), => c = ![]() (30´),
(30´), ![]() (29´)
(29´)
![]() (28´), => b =
(28´), => b = ![]() 1 (28´),
1 (28´), ![]() (24´), где
(24´), где
![]() - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
**********
Случай 3.
![]() (12)
(12)
![]() (13′)
(13′)
![]() (14)
(14)
![]() (15′) , которые также являются решениями уравнения
(15′) , которые также являются решениями уравнения
![]() (11).
(11).
Тогда сумма ![]() имеет вид:
имеет вид:
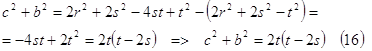
Учитывая (10) и (15), можно получить разность ![]() :
:
![]()
![]() -
-![]() =>
=> ![]() .
.
Выразим из (31) и (16) ![]() :
:
![]() =>
=> ![]() (32)
(32)
![]() =>
=> ![]() (33)
(33)
По условию ![]() должны быть взаимно простыми целыми нечетными числами, поэтому их общий множитель
должны быть взаимно простыми целыми нечетными числами, поэтому их общий множитель ![]() .
.
Т.о., ![]() имеют вид:
имеют вид:
![]() (34),
(34), ![]() (35), а их сумма
(35), а их сумма ![]() .
.
Т.к. из (4) c2 + b2 = 2 β, то ![]() и
и ![]() .
.
Из (15´) с учетом (20) выразим ![]() :
:
![]() , т.е.
, т.е. ![]() (24´).
(24´).
Т.о. ![]() ,
, ![]() , где
, где![]() , т.е.
, т.е.
![]() ,
,
![]() ,
,
выражения которых, с учетом (24´), полностью совпадают с (6) и (7), т. е. с уравнениями
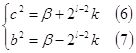
Теперь, с учетом (13′) и (14), найдем сумму ![]() :
:
![]()
т.к. ![]() , т.е.
, т.е. ![]() .
.
(Здесь чередование «плюса» и «минуса» такое же, как и у единицы в (20). В последующих действиях мы это учтем.)
Теперь, учитывая (23), получим значение для b2:
![]() ,т.к. из (20) получается
,т.к. из (20) получается
![]() .
.
Итак, ![]() (28), что для целых чисел неприемлемо. Этот случай нас не интересует.
(28), что для целых чисел неприемлемо. Этот случай нас не интересует.
*******
Тем не менее продолжим, т.к. результат, который мы получим, в дальнейшем нам пригодится.
Учитывая (26´), получим ![]() =>
=> ![]() (29´´).
(29´´).
Теперь, с учетом (29´´), можно получить окончательное выражение для с 2 (из (25´)):
![]() , т.е.
, т.е. ![]() (30´´).
(30´´).
Таким образом, уравнение ![]() (11), решениями которого являются (12), (13′), (14) и (15´), в конечном счете имеет следующие решения:
(11), решениями которого являются (12), (13′), (14) и (15´), в конечном счете имеет следующие решения:
![]() (30´´),
(30´´), ![]() ,
,
![]() (28),
(28), ![]() (24´),
(24´),
где ![]() - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
***********
Случай 4
Нетрудно догадаться, что если бы у уравнения (11) были бы решения, противоположные по знаку с решениями (12), (13′), (14) и (15´), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (30´´), (28), (29´´) и (24´), т.е.
![]() (30´´´), =>
(30´´´), => ![]() (30´´´),
(30´´´), ![]() (29´´´),
(29´´´), ![]() (28´), => b =
(28´), => b = ![]() (28´),
(28´), ![]() (24), где
(24), где
![]() - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
*******
Подведем некоторый итог. Нами рассмотрено 4 случая решений уравнения (11).
Обозначим снова следующие выражения буквами С, В, N, К:
![]() = С
= С
![]() = В
= В
![]() = N
= N
![]() = К
= К
Тогда эти первые 4 случая следующие:
1. (12) ![]() 2. (12´)
2. (12´) ![]() (30´)
(30´)
(13´) ![]() (28) (13)
(28) (13) ![]() (28´)
(28´)
(14) ![]() (29) (14´)
(29) (14´) ![]() (29´)
(29´)
(15) ![]() (24) (15´)
(24) (15´) ![]() (24´)
(24´)
3. (12) ![]() (30´´) 4. (12´)
(30´´) 4. (12´) ![]() (30´´´)
(30´´´)
(13´) ![]() (28) (13)
(28) (13) ![]() (28´)
(28´)
(14) ![]() (29´´) (14´)
(29´´) (14´) ![]() (29´´´)
(29´´´)
(15´) ![]() (24´) (15)
(24´) (15) ![]() (24).
(24).
Рассмотрим еще 4 случая.
5. с2 = С 6. с2 = - С 7. c2 = C 8. c2 = -C
b2 = - B b2 = B b2 = - B b2 = B
![]() = - N
= - N ![]() = N
= N ![]() = - N
= - N ![]() = N
= N
![]()
![]()
![]()
![]()
*******
Итак, рассмотрим случай 5.
Случай 5.
![]() (12),
(12),
![]() (13´),
(13´),
![]() (14´),
(14´),
![]() (15) , которые также являются решениями уравнения
(15) , которые также являются решениями уравнения
![]() (11).
(11).
Но данный случай аналогичен случаю 5 «Части 2» «Утверждения 1», где получены следующие решения уравнения (15):
![]() (41),
(41), ![]() , где
, где ![]() - взаимно простые нечетные целые
- взаимно простые нечетные целые ![]() (40),
(40), ![]() (38´), числа.
(38´), числа.
Следовательно, в данном рассматриваемом случае 5 у уравнения (11) следующие решения:
![]() (32) => b
(32) => b![]() (32),
(32), ![]() (24)
(24)
![]() (31) => с =
(31) => с = ![]() (31),
(31), ![]() (29´) ,
(29´) ,
где ![]() - взаимно простые целые нечетные числа.
- взаимно простые целые нечетные числа.
*******
Случай 6
Нетрудно догадаться, что если бы у уравнения (11) были решения, противоположные по знаку с решениями (12), (13′), (14´) и (15), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (32), (31), (29´) и (24), т.е.
![]() (31´),
(31´), ![]() (29),
(29),
![]() (32´),
(32´), ![]() (24´),
(24´),
где ![]() - взаимно простые целые нечетные числа.
- взаимно простые целые нечетные числа.
Но этот случай нас не интересует, т.к. с не является целым числом.
*******
Случай 7.
![]() (12),
(12),
![]() (13´),
(13´),
![]() (14´),
(14´),
![]() (15´), которые также являются решениями уравнения
(15´), которые также являются решениями уравнения
![]() (11).
(11).
Но данный случай аналогичен случаю 7 «Части 2» «Утверждения 1», где получены следующие решения уравнения (15):
![]() (40),
(40), ![]() (38´´´),
(38´´´),
![]() (41´´),
(41´´), ![]() (33´),
(33´),
где ![]() - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
Следовательно, в данном рассматриваемом случае 7 у уравнения (11) следующие решения:
![]() (31) => с =
(31) => с = ![]() (31),
(31), ![]() (29´´´) ,
(29´´´) ,
![]() (32´´) => b
(32´´) => b![]() (32´´),
(32´´), ![]() (24´), где
(24´), где ![]() -
-
взаимно простые целые нечетные числа.
*********
Случай 8
Нетрудно догадаться, что если бы у уравнения (11) были решения, противоположные по знаку с решениями (12), (13′), (14´) и (15´), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (32´´), (31), (29´´´) и (24´), т.е.
![]() (31´),
(31´), ![]() (29´´),
(29´´),
![]()
![]() ,
, ![]() (24),
(24),
где ![]() - взаимно простые целые нечетные числа.
- взаимно простые целые нечетные числа.
Но этот случай нас не интересует, т.к. с не является целым числом.
Таким образом, уравнение (11) ![]() , где c и b – взаимно простые целые нечетные числа, имеет решение (после анализа всех полученных решений) в следующих целых числах:
, где c и b – взаимно простые целые нечетные числа, имеет решение (после анализа всех полученных решений) в следующих целых числах:
а) ![]() ; b
; b![]() ;
; ![]() ;
; ![]() ;
;
б) ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
**********
Вывод
Итак, после анализа полученных решений в Случаях 1,…, 8, уравнение (11) ![]() , где c и b – взаимно простые целые нечетные числа, имеет решения в следующих целых числах:
, где c и b – взаимно простые целые нечетные числа, имеет решения в следующих целых числах:
а) ![]() ; b
; b![]() ;
; ![]() ;
; ![]() ;
;
б) ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
********
Таким образом, само исследование решений уравнения (11) в случаях 1, …, 8 при доказательстве Утверждения 3 и его результат полностью совпадают с исследованием решений уравнения (11) (в аналогичных случаях при доказательстве Утверждения 2) и с его результатом.
Действительно, вот, например, результаты исследований уравнения (11) в первых 4-х случаях Условия 1 (Утверждение 2, Часть 2):
1. (12) ![]() 2. (12´)
2. (12´) ![]() (30´)
(30´)
(13´) ![]() (28) (13)
(28) (13) ![]() (28´)
(28´)
(14) ![]() (29) (14´)
(29) (14´) ![]() (29´)
(29´)
(15) ![]() (24) (15´)
(24) (15´) ![]() (24´)
(24´)
3. (12) ![]() (30´´) 4. (12´)
(30´´) 4. (12´) ![]() (30´´´)
(30´´´)
(13´) ![]() (28) (13)
(28) (13) ![]() (28´)
(28´)
(14) ![]() (29´´) (14´)
(29´´) (14´) ![]() (29´´´)
(29´´´)
(15´) ![]() (24´) (15)
(24´) (15) ![]() (24).
(24).
А вот результаты исследований уравнения (11) в первых 4-х случаях Условия 1 (Утверждение 3, Часть 2):
1. (12) ![]() 2. (12´)
2. (12´) ![]() (30´)
(30´)
(13´) ![]() (28) (13)
(28) (13) ![]() (28´)
(28´)
(14) ![]() (29) (14´)
(29) (14´) ![]() (29´)
(29´)
(15) ![]() (24) (15´)
(24) (15´) ![]() (24´)
(24´)
3. (12) ![]() (30´´) 4. (12´)
(30´´) 4. (12´) ![]() (30´´´)
(30´´´)
(13´) ![]() (28) (13)
(28) (13) ![]() (28´)
(28´)
(14) ![]() (29´´) (14´)
(29´´) (14´) ![]() (29´´´)
(29´´´)
(15´) ![]() (24´) (15)
(24´) (15) ![]() (24).
(24).
Наблюдается полное совпадение результатов. То же самое совпадение результатов наблюдается и в следующих за ними 4-х случаях.
*********
Нетрудно понять, что остальные случаи с 9-го по 28-й в данном доказательстве Утверждения 3 (подобные вышерассмотренным случаям 9, …, 28 при доказательстве Утверждений 1 и 2) никаких новых решений нам не дадут, кроме как:
либо ![]() , либо
, либо ![]() , либо c и b не являются целыми числами, либо c и b – четные числа , чего не должно быть.
, либо c и b не являются целыми числами, либо c и b – четные числа , чего не должно быть.
********
Из этого набора решений уравнения (11), нас, естественно, интересуют только те, которые могут являться решениями уравнения (1) ![]() (1), где
(1), где ![]() - нечетное натуральное число, т.е. либо
- нечетное натуральное число, т.е. либо ![]() , либо
, либо ![]() , которые таковыми и являются.
, которые таковыми и являются.
*******
Вывод: 2-я часть «Утверждения 3» доказана.
В результате исследования уравнения (1), мы имеем:
Вывод:
1. Уравнение (1) ![]() (
(![]() ≥ 3 – нечетное натуральное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах
≥ 3 – нечетное натуральное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах ![]() ,
, ![]() и
и ![]() таких, чтобы
таких, чтобы ![]() - было четным,
- было четным, ![]() и
и ![]() - нечетными целыми числами.
- нечетными целыми числами.
Возможны случаи: либо ![]() , либо
, либо ![]() .
.
2. «Утверждение 3» нами полностью доказано.
*******
Примечание
Понятно, что приведенное сокращенное доказательство «Утверждения 3» (со ссылкой на предыдущее доказательство Утверждения 2), где рассматривается уравнение al+ b4 = c4 при ![]() ≥ 3 – нечетном натуральном и q = 4 = 2 m , где m = 2, распространяется и на показатель степени q = 2 m , где m > 2 – натуральном.
≥ 3 – нечетном натуральном и q = 4 = 2 m , где m = 2, распространяется и на показатель степени q = 2 m , где m > 2 – натуральном.
**********
На основании доказательства справедливости «Утверждения 1», «Утверждения 2» и «Утверждения 3» вытекает и справедливость «Общего утверждения».
ОБЩИЙ ВЫВОД
1. Уравнение ![]() (
(![]() ,
,![]() - натуральные числа) не имеет решений в отличных от нуля попарно взаимно простых целых числах
- натуральные числа) не имеет решений в отличных от нуля попарно взаимно простых целых числах ![]() ,
, ![]() и
и ![]() таких, чтобы
таких, чтобы ![]() - было четным,
- было четным, ![]() и
и ![]() - нечетными целыми числами.
- нечетными целыми числами.
2. Но есть и «исключение» из данного утверждения: среди этих чисел ![]() ,
, ![]() и
и ![]() может быть либо
может быть либо ![]() , либо
, либо ![]() .
.
Таким образом, «Общее утверждение» доказано.
ЛИТЕРАТУРА:
1. Алексеев С.Ф. Два обобщения классических формул // Квант. – 1988. - №10. – С. 23.
2.Постников М.М. Введение в теорию алгебраических чисел. – М., Наука. – 1982 - С. 13.
Май 2009 г., Скворцов А.П.
Уважаемые любители математики и специалисты!
Если не трудно, попробуйте разобраться с данной работой и по возможности ее оценить.
Если в ней есть что-то стоящее, интересное, то очень хотелось бы получить отзыв о данной работе.
Я убежден, что примененный мною метод в данной работе позволит провести анализ и некоторых других уравнений на их разрешимость в целых числах.
Предлагаю вашему вниманию перечень некоторых моих работ по физике и математике, с некоторыми из них ознакомлены специалисты некоторых ВУЗов г. Томска, с другими – учителя и учащиеся г. Колпашева. А работа по физике (я сам учитель физики) о существовании гипотетических гравитационно-временных волн («Гравитация и время») в популярном изложении опубликована на страницах журнала «Знак вопроса» №4-2004 г.
Работы по математике:
1. Построение с помощью циркуля и линейки отрезка, равного произведению двух других отрезков.
2. Построение с помощью циркуля и линейки отрезка, равного отношению двух других отрезков.
3. Нахождение действительных корней приведенного квадратного уравнения с помощью циркуля и линейки.
4. Решение уравнения ![]() в целых числах при
в целых числах при ![]() - натуральном.
- натуральном.
5. Доказательство неразрешимости в рациональных ненулевых числах уравнения р1+ р2 = р3, где произведение р1 р2 р3 = R3, R – рациональное число (или рациональная функция), р1, р2 и р3могут быть не только рациональными числами, но и рациональными функциями.
6. Доказательство неразрешимости в рациональных ненулевых числах системы
![]() р1+р2+р3 =р4
р1+р2+р3 =р4
р1 р2 р3 р4 = ![]() ,
,
где k может принимать значения k = 1; 2; 3; 4, и р1, р2 , р3и р4 могут быть не только рациональными числами, но и рациональными функциями.
Мне можно писать по электронному адресу: skvorsan@mail.ru
Мой почтовый адрес: 636460 г. Колпашево Томской обл.,
м/р-н Геолог, д.18, кв.11
тел.: 8 (38 254) 5 79 59.
С уважением, А.П. Скворцов.
Похожие работы
... , что возможно, наша цивилизация подойдет к концу прежде, чем удастся доказать Великую теорему Ферма. Доказательство Великой теоремы Ферма стало самым ценным призом в теории чисел, и поэтому не удивительно, что поиски его привели к некоторым наиболее захватывающим эпизодам в истории математики. В эти поиски оказались вовлеченными величайшие умы на нашей планеты, за доказательство назначались ...
... Декарт в первую очередь идеолог: он основатель философской школы, он формирует понятия, совершенствует систему буквенных обозначений, но в его творческом наследии мало новых конкретных приемов. В противоположность ему Пьер Ферма мало пишет, но по любому поводу может придумать массу остроумных математических трюков (см. там же “Теорема Ферма”, ”Принцип Ферма”, ”Метод бесконечного спуска Ферма”). ...
... Z 12 30 (15) При рассмотрении вопроса о Пифагоровых тройках не было целью составление таблиц этих троек. Ибо целью этой статьи является показ возможностей алгоритма решения Диофантовых уравнений. Решение уравнения Каталана Уравнение данного вида получается при попытке решения гипотезы Биля. Поэтому решение данного уравнения является как бы леммой гипотезы Биля. Ответ будет ...
... ) и теория диофантового приближения (раздел теории чисел, в котором изучаются приближения нуля значениями функций от конечного числа целочисленных аргументов). 2.6. Теон и Гипатия Учеными, завершившими цикл математиков Александрийской школы, были Теон (IV в.) и его дочь Гипатия (370—415). Теон проделал большую работу, комментируя труды Евклида и Птолемея. Что же касается Гипатии, то, по отзывам ...

0 комментариев