Полиномиальные системы

1.4.1 Полиномиальные системы

Полиномиальной системой мы будем называть автономную систему ОДУ

,  (25)

где - алгебраические полиномы по .

Какие системы ОДУ можно свести к полиномиальным и как это делается? Начнем с примера. Рассмотрим задачу Коши:

 (26)

 (27)

Вводя дополнительные переменные

  (28)

получаем следующую квадратичную задачу Коши:

 (29)

(30)

Теперь рассмотрим достаточно общий случай. Рассмотрим класс  сис-тем ОДУ (23), правые части которых можно представить в виде:

 (31)

где все функции , а также все функции

 (32)

являются алгебраическими полиномами по .

Любая система из  сводится к полиномиальной. Действительно, если в (23),(24) ввести дополнительные переменные  то:

(33)

 (34)

где все правые части

  (35)

- алгебраические полиномы по  с постоянными коэффициентами.

Уравнения кинетики, как правило, либо имеют вид (25), либо могут быть сведены к такой системе введением дополнительных переменных. Поэтому важно знать какие функции удовлетворяют полиномиальным системам, или, иначе говоря, насколько богаты содержанием модели, основанные на полиномиальных системах ОДУ.

Обсудим этот вопрос. Будем говорить, что скалярная функция скалярного аргумента удовлетворяет полиномиальной системе, если она является одной из компонент решения такой системы. Класс скалярных функций, удовлетворяющих полиномиальной системе назовем . За исключением некоторых теоретико-числовых функций (гамма-функция Эйлера, дзета-функция Римана и т.п.) остальные функции из известных математических справочников принадлежат классу .

Этот класс замкнут относительно операций  (сложение, вычитание, умножение, деление, дифференцирование, интегрирование, супер-позиция). Это означает, что если функции  принадлежат , то и любая их композиция, полученная при помощи конечного числа операций , также принадлежит .

1.4.2 Метод рядов Тейлора

Введем в рассмотрение оператор , сопоставляющий решению  задачи Коши (23), (24) его полином Тейлора

, (36)

порядка . Радиус сходимости ряда  обозначим .

Метод рядов Тейлора решения задачи Коши (23), (24) заключается в построении таблицы приближенных значений  по формулам:

,

,, (37)

где  - натуральные, , ,, а  удовлетворяют неравенствам .

Для программной реализации метода рядов Тейлора необходимы алгоритмы нахождения коэффициентов Тейлора и автоматического выбора величины шага интегрирования.

Нахождение коэффициентов Тейлора

Рассмотрим квадратичную задачу Коши

, (38)

, (39)

где  - вещественные или комплексные постоянные, а  - вещественная или комплексная переменная.

Подставляя в (38) разложение Тейлора

, (40)

получаем:

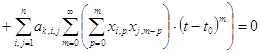(41)

Приводя подобные члены и приравнивая все коэффициенты полученного степенного ряда нулю, получаем искомые формулы:

;

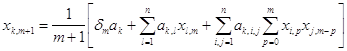, , , (42)

где , .

Аналогичные формулы легко вывести и для общего случая полиномиальной системы степени .

Оценка погрешности и выбор шага

Рассмотрим полиномиальную задачу Коши:

, (43)

, (44)

где , , , а максимальная степень полиномов  (степень системы (43)) равна .

Введем обозначения:

, ,  (45)

и будем предполагать, что .

Теорема.

Решение  задачи (43), (44) голоморфно в круге  и удовлетворяет там неравенствам:

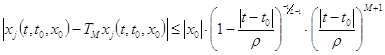, (46)

где

, ,  (47)

Используя эту теорему несложно построить алгоритм автоматического выбора шага в методе рядов Тейлора по заданной пользователем границе абсолютной (или относительной) погрешности.

 

1.4.3 Метод Рунге-Кутта

Этим методам посвящено много работ, и они хорошо изложены в много-численных учебниках (см., например, [2,3]).

2. Модели осциллирующих процессов в живой природе

 

2.1 Модель Лотки

 

2.1.1 Осциллирующие химические реакции

В некоторых химических реакциях концентрации реагентов осциллируют в следующем смысле. Соединение каких-то начальных веществ приводит к их химическому взаимодействию, в результате чего образуются новые вещества, которые также начинают взаимодействовать с другими реагента-ми. В течении всех этих реакций концентрации реагентов колеблются и, на-конец, все химические преобразования завершаются и в качестве результата остаются какие-то определенные вещества, которые уже не реагируют между собой. Первая математическая модель осциллирующих химических реакций была предложена в работе Лотки [7].

Рассматривается математическая модель взаимодействия на молекулярном уровне веществ  на основе следующих предположений:

1. При взаимодействии с молекулой вещества  молекула вещества  превращается в молекулу вещества . Это описывают в форме молекулярной ре-акции:

(1)

Такую реакцию относят к классу автокаталитических, так как наличие вещества  обеспечивает превращение другого вещества в .

2. При взаимодействии с молекулой вещества  молекула вещества  пре-вращается в молекулу вещества , то есть происходит автокаталитическая молекулярная реакция:

(2)

3. Вещество  в то же время необратимо распадается, превращаясь в вещество , то есть происходит молекулярная реакция

(3)

4. Скорости протекания реакций (1), (2), (3) пропорциональны концентрациям веществ в левых частях этих реакций, то есть равны соответственно:

, , , (4)

где символами , ,  обозначены концентрации веществ , ,  со-ответственно, а коэффициенты  - положительные числа.

5. Скорость изменения концентрации каждого вещества равна сумме скоростей изменения концентраций этого вещества во всех реакциях, в которых оно участвует.

Из условий 1-5 следуют равенства:

,

,

,

, (5)

где  - концентрация вещества . Это система ОДУ Лотки.