Постановки задачи идентификации и функционалы МНК

3.2 Постановки задачи идентификации и функционалы МНК

Для конкретных биологических или иных моделей проводят реальные эксперименты по определению величин , от которых зависят функционалы типа (20) п.1.3. Каждый реальный эксперимент имеет и свои возможности (часто весьма ограниченные) и свою цену (возможно высокую) определения каждой величины .

Естественно поэтому использовать различные функционалы, зависящие от того или иного набора величин . Мы рассмотрим три функционала. Пер-вые два из них ориентированы на различные типы экспериментов с весьма ограниченными возможностями, а третий является их обобщением.

В эксперименте первого типа, при одном и том же начальном данном  измеряются значения

(5)

одной из переменных  в различные моменты , .

В эксперименте второго типа, при начальных данных ,, из-меряются значения

, (6)

 величин , в один и тот же момент времени .

В эксперименте третьего типа, при начальных данных ,, из-меряются значения

(7)

 величин , в моменты времени , ,.

Соответствующие функционалы равны:

, (8)

, (9)

, (10)

где  - фиксированные весовые коэффициенты.

Градиентные уравнения и соответствующие начальные условия для этих функционалов следующие:

, (11)

, (12)

 (13)

, (14)

3.3 Как ускорить вычисления

Опыт реальных вычислений показывает, что минимизация функционала методом градиентных уравнений естественно делится на два этапа. На первом этапе происходит быстрое уменьшение функционала. На втором этапе это уменьшение становится все более медленным, и процесс нахождения достаточно точного приближения параметров, соответствующих локальному минимуму функционала, может потребовать неприемлемо больших затрат машинного времени.

Для того, чтобы ускорить вычисления на втором этапе, необходимо ускорить численное интегрирование исходных уравнений, уравнений в вариациях и градиентных уравнений. Исходные уравнения и уравнения в вариациях, как правило, полиномиальные и для их численного интегрирования можно использовать метод рядов Тейлора.

Градиентные уравнения не полиномиальные, и на первом из упомянутых выше этапов их естественно интегрировать методами Рунге-Кутта. На втором этапе идентифицируемые параметры изменяются медленно и правые части градиентных уравнений можно аппроксимировать полиномами по этим параметрам в окрестности некоторого их текущего значения.

Эта аппроксимация достаточно точна только на некотором промежутке изменения , поэтому ее нужно время от времени строить заново в окрестности очередного текущего значения параметров. На соответствующих промежутках изменения  приближенные полиномиальные градиентные уравнения можно интегрировать методом рядов Тейлора.

Отметим, что построение каждой аппроксимации градиентных уравнений требует многократного численного решения исходных уравнений и уравнений в вариациях, для чего можно использовать метод рядов Тейлора.

Перейдем к формулам. Уравнения точной градиентной задачи Коши

(15)

, , (16)

где , мы хотим заменить на приближенные градиентные уравнения:

, , (17)

где  - полином по , а  - набор его коэффициентов.

При этом мы хотим, чтобы величины

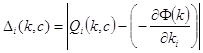,  (18)

были достаточно малыми при

, (19)

где  - некоторое фиксированное число. Коэффициенты  поли-нома  можно найти методом наименьших квадратов с функционалом:

, (20)

где , , а  - весовые коэффициенты.

Отметим, что при малых  в качестве  можно рассмотреть полином степени 3 или 4, а при больших  и/или  - полином степени 2.

Похожие работы

Устройства генерирования и канализации субмиллиметровых волн

Скачать

117222

0

10

... , то необходимость в дополнительной линии передачи вообще отпадает при передаче энергии на сотни километров, поскольку вся излучаемая энергия может быть перехвачена приемным устройством с апертурой приемлемых размеров. В диапазоне субмиллиметровых волн отношение допустимых размеров апертур к длине волны заметно уменьшается, тем не менее в ряде случаев подобные квазиоптические линии передачи могут ...