ОСНОВНЫЕ ПОНЯТИЯ

2 ОСНОВНЫЕ ПОНЯТИЯ

Многогранной поверхностью в пространстве называется поверхность, составленная из конечного числа многоугольников. Эти многоугольники являются гранями многогранной поверхности, а стороны граней — ее ребрами.

Две фигуры (в частности два многогранника) называют конгруэнтными, если они эквивалентны друг другу, то есть совпадают при наложении.

Если у многогранника есть ребро, принадлежащее всего одной грани, то это – многогранник с краем. Если же каждое ребро принадлежит двум граням, многогранник называют замкнутый. У замкнутого многогранника края нет.

Многогранные поверхности с самопересечениями - это такие поверхности, у которых грани могут иметь общие точки, не являющиеся вершинами данной многогранной поверхности и не принадлежащие ее ребрам.

Многогранную поверхность называют выпуклой, если плоскость, проходящую через любую ее грань, оставляет остальные ее грани по одну сторону.

Многогранная поверхность называется изгибаемой, если непрерывным изменением двугранных углов при ее ребрах можно изменить пространственную форму поверхности. Поэтому незамкнутая многогранная поверхность, составленная из двух треугольников, соединенных вдоль одного ребра, является изгибаемой.

Изгибанием многогранника называется такая непрерывная его деформация, при которой изменяется хотя бы один из двугранных углов при ребрах, но грани остаются конгруэнтными (равными) исходным. Иначе говоря, в теории изгибаний грани многогранника рассматриваются как абсолютно твердые пластинки, способные вращаться вокруг ребер и вершин. На "инженерном" языке это означает, что вдоль ребер грани имеют шарнирные связи, а вершины многогранника считаются сферическими шарнирами. Если многогранник допускает деформацию такого вида, он называется изгибаемым, в противном случае — неизгибаемым. Движения многогранника в пространстве как твёрдого тела не являются его изгибаниями, так как при таком движении ни один двугранный угол не изменяется. Поэтому такие движения иногда называют тривиальными изгибаниями, а те деформации, о которых шла речь в определении изгибаний, называют нетривиальными изгибаниями. Очевидно, требование изменения в ходе нетривиального изгибания хотя бы одного двугранного угла можно заменить требованием изменения хотя бы одной диагонали многогранника.

Возможность простого перемещения многогранника в пространстве как твёрдого тела, т. е. без изменения его двугранных углов, используется для фиксации положения каких-либо «элементов» многогранника в ходе его изгибания. Делается это так: к деформации нетривиального изгибания многогранника добавляют движение, подобранное так, чтобы рассматриваемый элемент вернулся в исходное положение. Пусть, например, требуется, чтобы данная треугольная грань ABC была неподвижна. Если после деформации изгибания грань «ушла» из своего исходного положения, то сначала параллельным переносом вернём, скажем, точку A из нового в старое её положение, затем вращением вокруг точки A приведём в совпадение с прежними положениями вершины B и C.

Простейший пример изгибания многогранника — открытие или закрытие книги с твердой обложкой (многогранник может иметь край). Примеры посложнее: трёхгранный угол неизгибаем, а n-гранный угол при п>3 изгибаем. Если многогранник ещё сложнее, а особенно если он замкнутый, т. е. не имеет края, исследование его изгибаемости — сложная задача, так как изгибания всех многогранных углов должны быть согласованы между собой.

Октаэдр – правильный многогранник, который представляет собой четырехугольную бипирамиду. Октаэдр имеет 12 ребер, 6 вершин и 8 граней.

Октаэдр Брикара – это изгибаемый октаэдр, имеющий самопересечения

Флексором называется изгибаемая многогранная поверхность. Наименьшее число вершин среди всех замкнутых изгибаемых многогранных поверхностей без самопересечений имеет многогранная поверхность Штеффена. Другими словами, если замкнутая многогранная поверхность без самопересечений имеет менее девяти вершин, то она не является изгибаемой.

3. ИЗГИБАЕМЫЕ МНОГОГРАННИКИ КОННЕЛЛИ

рис. 5

рис. 4

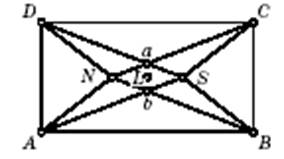
Рис.3

Изгибаемые многогранники Коннелли – это изгибаемые многогранники, которые не имеют самопересечений (т. е. являются вложенными в пространство). Основная идея — попытаться построить изгибаемый многогранник, устранив самопересечения в октаэдрах Брикара. Рассмотрим изгибаемый октаэдр Брикара первого типа, у которого грани дважды покрывают прямоугольник ABCD (рис. 3); L — точка пересечения диагоналей прямоугольника, через которую перпендикулярно к плоскости чертежа проходит ось симметрии l четырёх-звенника ABCD. Сначала сведём к минимуму возможные самопересечения. Для этого в четырёхгранном угле NABCD заменим каждую грань тремя боковыми гранями тетраэдров, обращённых вершинами вверх, оставив рёбра основания на своём месте в прямоугольнике, причём выберем расположения всех 12 граней так, чтобы они между собой не пересекались (для чего достаточно, чтобы вершины тетраэдров проектировались внутрь треугольников, которые они заменяют). Получим многогранник, составленный из четырёх тетраэдров без основания, как на рис. 4, и назовём этот многогранник «крышкой».

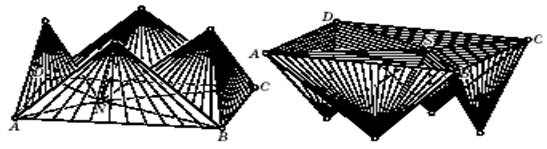
Рис.4

Аналогичным образом заменим грани четырёхгранного угла SABCD тетраэдрами вершинами вниз и получим «дно» будущего многогранника (рис. 5).

При изгибании четырёхгранных углов NABCD и SABCD их рёбра как-то перемещаются, и они автоматически определяют движения боковых граней построенных тетраэдров.

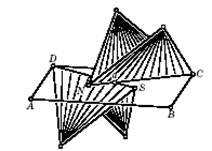
Рис.5

«Крышка» и «дно» склеены между собой по сторонам прямоугольника ABCD, и они вместе образуют замкнутый изгибаемый многогранник Q, состоящий из 24 боковых граней 8 тетраэдров. В отдельности на «крышке» и «дне» по построению самопересечений нет. Боковые грани и рёбра тетраэдров «крышки» и «дна» располагаются по разные стороны от общей плоскости их оснований, поэтому они тоже не пересекаются. Но рёбра на основании тетраэдров остались те же, что были в прямоугольнике на рис. 3. Видно, что есть всего две точки самопересечения — точки a и b. Наша задача — убрать эти самопересечения. В многограннике Q самопересечение выглядит как на рис. 6, т. е. фактически оно является самокасанием: в точке a касаются рёбра двух двугранных углов. Коннелли сумел изменить один двугранный угол в окрестности точки a так, чтобы исчезло самокасание, а новые элементы конструкции изгибались согласованно с изгибанием изменённого двугранного угла, состоящим в непрерывном изменении раствора двугранного угла.

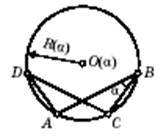
Рис.7

Для этого рассмотрим октаэдр Брикара второго типа. Пусть дан самопересекающийся плоский четырёхзвенный механизм ABCD с равными противоположными сторонами AB = CD, BC=AD (рис. 7). Легко показать, что вершины этого четырёхугольника являются вершинами равнобочной трапеции, поэтому вокруг ABCD можно описать окружность. Центр O и радиус R окружности зависят от a = ZABC. Четырёхзвенник ABCD может изменять свою форму с сохранением длин своих сторон (т. е. он может изгибаться), оставаясь на плоскости и имея сторону DC в неподвижном положении. При этом в новых положениях вершины четырёхугольника по-прежнему будут вершинами равнобочной трапеции и новое положение центра O(a) описанной окружности и её радиус R(a) при изгибании четырёхугольника ABCD на плоскости изменяются непрерывно вместе с a. Возьмём теперь над и под точкой O(a) две точки N и S на одинаковом расстоянии h(a) от O(a) (можно и на разных расстояниях, с соответствующими изменениями в дальнейших рассуждениях), таком, чтобы R²(a) + h²(a) = d² = const и соединим N(a) и S(a) отрезками длины d с точками A(a), B(a), C и D. После «обшивки» каркаса плоскими треугольниками получится октаэдр P, у которого есть плоскость симметрии, проходящая через точки N и S перпендикулярно прямой AC, т. е. мы получили октаэдр Брикара второго типа. Его изгибания определяются изгибаниями плоского четырёхзвенногомеханизма ABCD. Удалим из P две грани, дающие самопересечения: NDC и SDC. Останется многогранник Р' с краем, изображённый на рис. 8. Хотя ребра CD и нет, в ходе изгибания многогранника Р' как части P расстояние CD остаётся постоянным, так как оно равно длине ребра CD в октаэдре P.

При этом же изгибании расстояние NS, равное 2h(a), изменяется, поэтому изменяется угол между плоскостями удалённых граней NDC и SDC, причём точки D и C при этом можно считать остающимися на месте. Используем это обстоятельство для того, чтобы изменить двугранный угол на рис. 6, вставив туда соответствующим образом подобранный многогранник Р', который для краткости и большей ясности будем называть «зарубкой Коннелли». Пусть T — биссекторная плоскость, скажем, верхнего двугранного угла на рис. 6. Расположим четырёхзвенник ABCD на плоскости T так, чтобы отрезок DC шёл по ребру двугранного угла, отрезки ND и NC были на одной полуплоскости, а DS и CS были на другой полуплоскости двугранного угла. Части ND и NC, SD и SC края многогранника Р' — «зарубки Коннелли» — прилегают к соответствующим частям граней двугранного угла. Изменение величины b двугранного угла приводит к изгибанию многогранника Р', согласованному с движением граней двугранного угла, в который он был встроен (т. е. рёбра ND и NC, SD и SC края многогранника Р' не изменяют свою длину и остаются на гранях двугранного угла). Расположение точек D и C на ребре двугранного угла может быть выбрано так, чтобы точка a оказалась на отрезке DC, не попадая, однако, на ребро AB, т. е. чтобы изменённый верхний двугранный угол на рис. 6 не касался нижнего двугранного угла. Такое же построение можно провести и в окрестности точки b — второй точки самокасания, причём размеры встроенного многогранника Р' можно подобрать так, чтобы в пределах некоторого изменения раствора двугранного угла не появились новые самопересечения. Таким образом получится изгибаемый многогранник без самопересечений с 26 вершинами.

Рис.10

Легко видеть, что эту конструкцию можно сразу же упростить, а именно, в исходном дважды покрытом прямоугольнике можно оставить на месте грани AND и BSC (см. рис. 3), не заменяя их тетраэдрами, тогда получится изгибаемый многогранник с 24 вершинами.

Существенное упрощение получается, если в исходном октаэдре Брикара добавлять тетраэдры так, чтобы была необходимость использовать «зарубку Коннелли» только один раз, как это предложили П. Делинь и Н. Кёйпер. Делается это так. Отправным положением будет изгибаемый октаэдр Брикара первого типа, изображённый на рис. 9. На нём вершины A и C лежат на горизонтальной плоскости (условно с координатой z = 0), вершины В' и D' подняты на высоту е>0, а вершины N' и S' — на высоту 6>е и всё это проектируется ортогонально на прямоугольник рис. 3 (где L по-прежнему обозначает точку пересечения этого прямоугольника с вертикально расположенной осью симметрии рассматриваемого октаэдра). В новом положении ребро AS' проходит под ребром N'B', ребро N'C — под ребром S'D', так что прежних точек самопересечения нет, но есть новые пересечения граней. Построим теперь «дно» следующим образом: в исходном четырёхгранном угле S'AB'CD' с вершиной S' заменим грань S'CD' тетраэдром вершиной вниз (рис. 10). Краем построенного многогранника

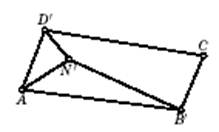
Рис.11

является четырёхугольник AB'CD', но теперь есть «яма» в виде тетраэдра S₀S'CD'. Далее строим «крышу» так. Над фигурой рис. 11 возьмём две точки T и K и построим неполные

Рис.12

пирамиды с гранями N'D'T и D'CT, N'B¹ K и В'СК. Получится многогранник без самопересечений и с двумя четырёхугольными краями AB'CD' и N'KCT (рис. 12). Он

рис. 12

пересекается с построенным ранее «дном» только вдоль контура AB'CD' и после склеивания «крышки» с «дном» вдоль этого контура получится многогранник (обозначим его Г) без самопересечений и с одним четырёхугольным краем N'KCT.

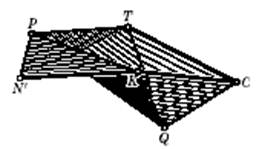
Рис.13

Многогранник Г изгибается, причём его исходные вершины просто повторяют те движения, которые были у начального изгибаемого октаэдра Брикара первого типа на рис. 9, поэтому, в частности, расстояние N'C остаётся постоянным, так как оно соответствует длине ребра N'C исходного октаэдра. Теперь подберём «зарубку Коннелли» так, чтобы её добавлением закрыть отверстие с краем N'KCT. Для этого выберем положения точек T и K с условием TC = TN=KN=КС, что вполне возможно. Возьмём «зарубку Коннелли» как на рис. 8, но с изменёнными в соответствии с рис. 13 обозначениями вершин и со сторонами TN' = TP = TQ = TC = KN' = KC = KP = KQ. Можем считать, что изгибания многогранника Г происходят с сохранением

рис. 13

плоскости трёх вершин N', K, T, и точки K и T перемещаются по фиксированной прямой KT так, что середина отрезка KT остаётся неподвижной. Этими условиями движения точек K, T, N' и C, а значит, и остальных вершин многогранника Г определены однозначно. При этих же условиях изгибания «зарубки Коннелли» тоже определяются однозначно, поэтому движения её вершин K, T, N' и C будут теми же самыми, что и у соответствующих вершин многогранника Г. Это значит, что когда мы склеим край N'KCT «зарубки Коннелли» с таким же краем многогранника Г, изгибания Г и «зарубки» будут согласованными. Остаётся позаботиться, чтобы «зарубка» поместилась в «яму», пересекаясь с многогранником Г только по их общему краю, для чего нужно выбрать то положение плоскости механизма PQCN', когда точка Q окажется внутри тетраэдра S₀D'S'C, а точка P — выше треугольника AS' D', и тогда получится изгибаемый многогранник без самопересечений, имеющий 11 вершин и 18 граней.