Навигация
Программная реализация итерационных методов
3. Программная реализация итерационных методов
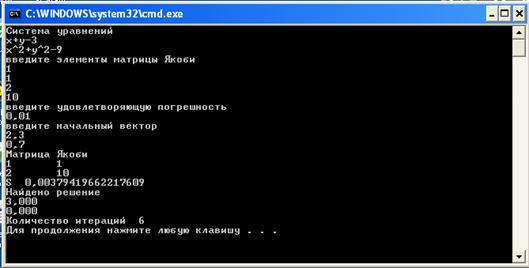
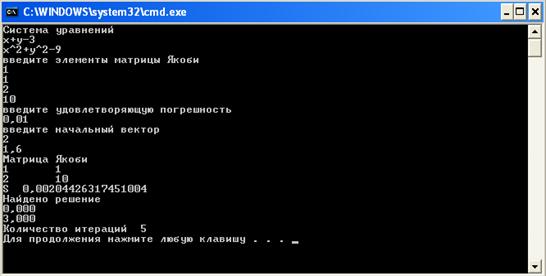
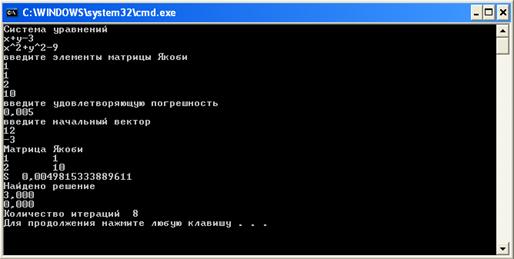
Реализация алгоритмов итерационных методов решения систем нелинейных уравнений будет показана на примере системы:
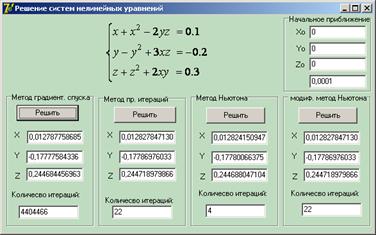
3.1 Метод простых итераций
Приведём систему к виду:
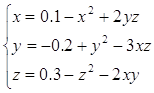
Проверим условие сходимости метода простых итераций.
Для этого построим матрицу Якоби
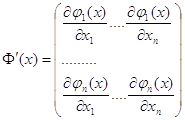
> f1:=0.1-x0^2+2*y0*z0; ![]()
f2:=-0.2+y0^2-3*x0*z0; ![]()
f3:=0.3-z0^2-2*x0*y0; ![]()
> f1x:=diff(f1,x0):
> f1y:=diff(f1,y0):
> f1z:=diff(f1,z0):
> f2x:=diff(f2,x0):
> f2y:=diff(f2,y0):
> f2z:=diff(f2,z0):
> f3x:=diff(f3,x0):
> f3y:=diff(f3,y0):
> f3z:=diff(f3,z0):
> A:=<<f1x|f1y|f1z>,<f2x|f2y|f2z>,<f3x|f3y|f3z>>;
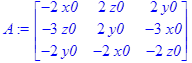
И найдём ей обратную, норму обратной матрицы сначала в общем виде:
> A1:=MatrixInverse(A);
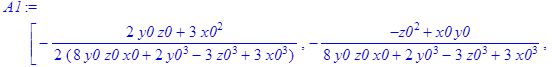
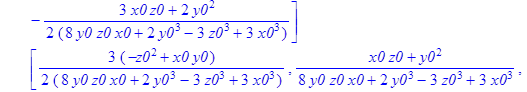
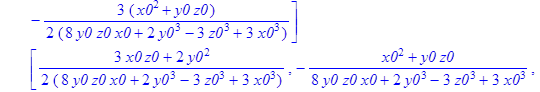
![]()
> norma:=MatrixNorm(A1,1);
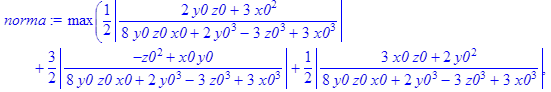
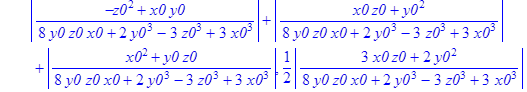
![]()
Найдём значения ![]() при которых норма обратной матрицы Якоби меньше единицы.
при которых норма обратной матрицы Якоби меньше единицы.
> x0:=1; y0:=1; z0:=1;
![]()
![]()
![]()
> norma;
![]()
Это означает, что по формулам
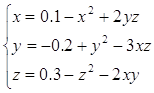
последовательность итераций будет сходиться к решению системы уравнений.
Построим итерационную последовательность
> restart;
> with(LinearAlgebra):
> x0:=0:
y0:=0:
z0:=0:
> x:=0.1-x0^2+2*y0*z0;
y:=-0.2+y0^2-3*x0*z0;
z:=0.3-z0^2-2*x0*y0;
i:=1;
![]()
![]()
![]()
> while (abs(x-x0)>0.0001)and(abs(y-y0)>0.0001)and(abs(z-z0)>0.0001) do
x0:=x:
y0:=y:
z0:=z:
x:=0.1-x0^2+2*y0*z0;
y:=-0.2+y0^2-3*x0*z0;
z:=0.3-z0^2-2*x0*y0;
i:=i+1;
end do:
Получили ответ:
![]()
![]()
![]()
Количество итераций:
![]()
Погрешность решения:
![]()
Отсюда можно получить коэффициент сжатия последовательности:
При ![]()
> P:= 0.3*q^22/(1-q)-0.0001;
![]()
> q:= fsolve(P);
![]()
Таким образом можно сказать, что было построено сжимающее отображение, для которого выполняется условие Липшица
![]()
Текст программы:
procedure TForm1.Button3Click(Sender: TObject);
var i:integer;
x0,y0,z0,x,y,z,eps: real;
begin
x0:=StrToFloat(Edit1.Text);
y0:=StrToFloat(Edit2.text);
z0:=StrToFloat(Edit3.Text);
eps:=StrToFloat(Edit20.Text);
i:=1;
x:=0.1-x0*x0+2*y0*z0;
y:=-0.2+y0*y0-3*x0*z0;
z:=0.3-z0*z0-2*x0*y0;
repeat
i:=i+1;
x0:=x;
y0:=y;
z0:=z;
x:=0.1-x0*x0+2*y*z;
y:=-0.2+y0*y0-3*x0*z0;
z:=0.3-z0*z0-2*x0*y0;
until ((abs(x-x0)<eps)and(abs(y-y0)<eps)and(abs(z-z0)<eps));
Edit8.Text:=FloatToStr(x);
Edit9.Text:=FloatToStr(y);
Edit10.Text:=FloatToStr(z);
Edit11.Text:=IntToStr(i);
end;
Преобразование Эйткена на примере метода простых итереций:
> restart;
> x0:=0:
y0:=0:
z0:=0:
> f1:=0.1-x0^2+2*y0*z0;
f2:=-0.2+y0^2-3*x0*z0;
f3:=0.3-z0^2-2*x0*y0;
ff1:=0.1-f1^2+2*f2*f3;
ff2:=-0.2+f2^2-3*f1*f3;
ff3:=0.3-f3^2-2*f1*f2;
x:=(x0*ff1-f1^2)/(ff1-2*f1+x0);
y:=(y0*ff2-f2^2)/(ff2-2*f2+y0);
z:=(z0*ff3-f3^2)/(ff3-2*f3+z0);
i:=1;
![]()
![]()
![]()
while (abs(x-x0)>0.0001)do
x0:=x:
y0:=y:
z0:=z:
f1:=0.1-x0^2+2*y0*z0;
f2:=-0.2+y0^2-3*x0*z0;
f3:=0.3-z0^2-2*x0*y0;
ff1:=0.1-f1^2+2*f2*f3;
ff2:=-0.2+f2^2-3*f1*f3;
ff3:=0.3-f3^2-2*f1*f2;
x:=(x0*ff1-f1^2)/(ff1-2*f1+x0);
y:=(y0*ff2-f2^2)/(ff2-2*f2+y0);
z:=(z0*ff3-f3^2)/(ff3-2*f3+z0):
i:=i+1;
end do:
Получили ответ:
![]()
![]()
![]()
Количество итераций:
![]()
Похожие работы
... метод Бройдена, написана программа реализующая его. СПИСОК ЛИТЕРАТУРЫ 1. С.Л. Подвальный, Л.В. Холопкина. Вычислительная математика- учебное пособие ВГТУ, 2004 - 147 с. 2. Методы решения систем нелинейных уравнений. Метод Ньютона. Его реализации и модификации. - Электрон. дан. – Режим доступа: www.exponenta.ru/educat/referat/XVkonkurs/15/index.asp. ПРИЛОЖЕНИЕ Текст программы ...
... –0.6 = 0 9. 10. ( x -1)3 + 0.5ex = 0 11. 12. x5 –3x2 + 1 = 0 13. x3 –4x2 –10x –10 = 0 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. x 4- 2.9x3 +0.1x2 + 5.8x - 4.2=0 25. x4+2.83x3- 4.5x2-64x-20=0 26. МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 1. Постановка задачи Пусть требуется решить систему n ...
... 1040, мы все еще получаем сходимость, при количестве итераций порядка 130. 4 Анализ результатов, выводы Целью нашего исследование было сравнение методов простой итерации и Ньютона для решения систем из двух нелинейных уравнений по числу итераций, времени сходимости в зависимости от выбора начального приближения к решению и допустимой ошибки. Зависимость этих параметров от выбора начального ...
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...
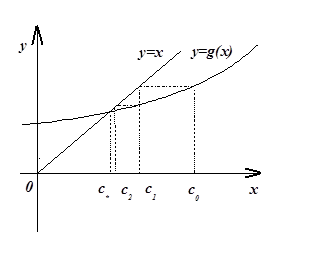
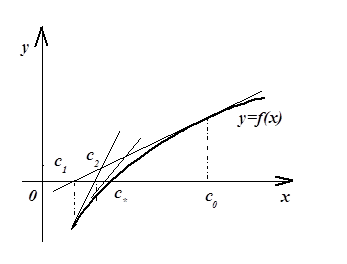
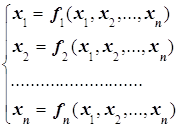
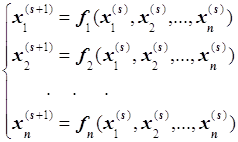
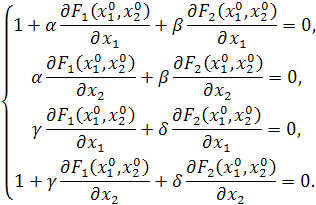



0 комментариев