Навигация
3.3 Метод Ньютона
Строим матрицу Якоби:
> restart;
> with(LinearAlgebra):
> f1:=0.1-x0^2+2*y0*z0-x0;
![]()
> f2:=-0.2+y0^2-3*x0*z0-y0;
![]()
> f3:=0.3-z0^2-2*x0*y0-z0;
![]()
> f1x:=diff(f1,x0);
> f1y:=diff(f1,y0);
> f1z:=diff(f1,z0);
> f2x:=diff(f2,x0);
> f2y:=diff(f2,y0);
> f2z:=diff(f2,z0);
> f3x:=diff(f3,x0);
> f3y:=diff(f3,y0);
> f3z:=diff(f3,z0);
> A:=<<f1x|f1y|f1z>,<f2x|f2y|f2z>,<f3x|f3y|f3z>>;
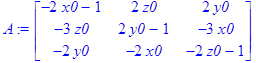
Выбираем начальное приближение, близкое к уже известному нам корню и строим последовательность:
> x0:=0;y0:=0;z0:=0;
![]()
![]()
![]()
> A:=A;
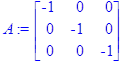
> A1:=A^(-1);
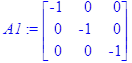
> f:=<f1,f2,f3>;
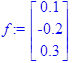
> X0:=<x0,y0,z0>:
> X:=Add(X0,(Multiply(A1,f)),1,-1);

> X0:=X;
> x0:=X[1];y0:=X[2];z0:=X[3];
> A:=<<f1x|f1y|f1z>,<f2x|f2y|f2z>,<f3x|f3y|f3z>>;
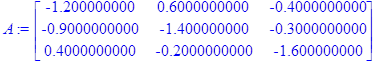
> A1:=A^(-1);
> f:=<f1,f2,f3>;
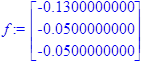
> X:=Add(X0,(Multiply(A1,f)),1,-1);
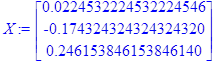
> i:=2:
> while (Norm(f))>0.0001 do
X0:=X;
x0:=X[1];y0:=X[2];z0:=X[3];
A:=<<f1x|f1y|f1z>,<f2x|f2y|f2z>,<f3x|f3y|f3z>>;
A1:=A^(-1);
f:=<f1,f2,f3>;
X:=Add(X0,(Multiply(A1,f)),1,-1);
i:=i+1;
end do:
> X:=X;
Получили ответ:

Количество итераций:
![]()
Текст программы
procedure TForm1.Button4Click(Sender: TObject);
type mas=array[1..3]of real;
matr=array[1..3,1..3]of real;
var a,a1:matr;
i,j:integer;
x,y,z,eps:real;
f,xk,xkk,temp:mas;
procedure jacobi(x,y,z:real; var a:matr);
begin
a[1,1]:=-2*x-1;
a[1,2]:=2*z;
a[1,3]:=2*y;
a[2,1]:=-3*z;
a[2,2]:=2*y-1;
a[2,3]:=-3*x;
a[3,1]:=-2*y;
a[3,2]:=-2*x;
a[3,3]:=-2*z-1;
end;
procedure inverse(a:matr;var a1:matr);
var i,j:integer;
det:real;
s:matr;
begin
det:=a[1,1]*a[2,2]*a[3,3]+a[2,1]*a[3,2]*a[1,3]+a[1,2]*a[2,3]*a[3,1]-a[3,1]*a[2,2]*a[1,3]-a[3,2]*a[2,3]*a[1,1]-a[2,1]*a[1,2]*a[3,3];
s[1,1]:=a[2,2]*a[3,3]-a[2,3]*a[3,2];
s[1,2]:=-a[1,2]*a[3,3]+a[1,3]*a[3,2];
s[1,3]:=a[1,2]*a[2,3]-a[1,3]*a[2,2];
s[2,1]:=-a[2,1]*a[3,3]+a[2,3]*a[3,1];
s[2,2]:=a[1,1]*a[3,3]-a[1,3]*a[3,1];
s[2,3]:=-a[1,1]*a[2,3]+a[1,3]*a[2,1];
s[3,1]:=a[2,1]*a[3,2]-a[2,2]*a[3,1];
s[3,2]:=-a[1,1]*a[3,2]+a[1,2]*a[3,1];
s[3,3]:=a[1,1]*a[2,2]-a[1,2]*a[2,1];
for i:=1 to 3 do
for j:=1 to 3 do
a1[i,j]:=(1/det)*s[i,j];
end;
procedure fx(x,y,z:real; var f:mas);
begin
f[1]:=-x-x*x+2*y*z+0.1;
f[2]:=-y+y*y-3*x*z-0.2;
f[3]:=-z-z*z-2*x*y+0.3;
end;
procedure minus(x,y:mas; var z:mas);
var i:integer;
begin
for i:=1 to 3 do
z[i]:=x[i]-y[i];
end;
function max(f:mas):real;
var p:real;
i:integer;
begin
p:=0;
for i:=1 to 3 do
if abs(f[i])>p then p:=abs(f[i]);
max:=p;
end;
procedure mult(a:matr;b:mas;var c:mas);
begin
c[1]:=a[1,1]*b[1]+a[1,2]*b[2]+a[1,3]*b[3];
c[2]:=a[2,1]*b[1]+a[2,2]*b[2]+a[2,3]*b[3];
c[3]:=a[3,1]*b[1]+a[3,2]*b[2]+a[3,3]*b[3];
end;
begin
xk[1]:=StrToFloat(Edit1.Text);
xk[2]:=StrToFloat(Edit2.Text);
xk[3]:=StrToFloat(Edit3.Text);
eps:=StrToFloat(Edit20.Text);
i:=0;
repeat
fx(xk[1],xk[2],xk[3],f);
jacobi(xk[1],xk[2],xk[3],a);
inverse(a,a1);
mult(a1,f,temp);
minus(xk,temp,xk);
i:=i+1;
until max(f)<eps;
Edit12.Text:=FloatToStr(xk[1]);
Edit13.Text:=FloatToStr(xk[2]);
Edit14.Text:=FloatToStr(xk[3]);
Edit15.Text:=IntToStr(i);
end;
Похожие работы
... метод Бройдена, написана программа реализующая его. СПИСОК ЛИТЕРАТУРЫ 1. С.Л. Подвальный, Л.В. Холопкина. Вычислительная математика- учебное пособие ВГТУ, 2004 - 147 с. 2. Методы решения систем нелинейных уравнений. Метод Ньютона. Его реализации и модификации. - Электрон. дан. – Режим доступа: www.exponenta.ru/educat/referat/XVkonkurs/15/index.asp. ПРИЛОЖЕНИЕ Текст программы ...
... –0.6 = 0 9. 10. ( x -1)3 + 0.5ex = 0 11. 12. x5 –3x2 + 1 = 0 13. x3 –4x2 –10x –10 = 0 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. x 4- 2.9x3 +0.1x2 + 5.8x - 4.2=0 25. x4+2.83x3- 4.5x2-64x-20=0 26. МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 1. Постановка задачи Пусть требуется решить систему n ...
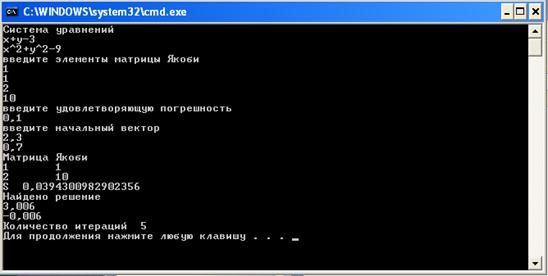
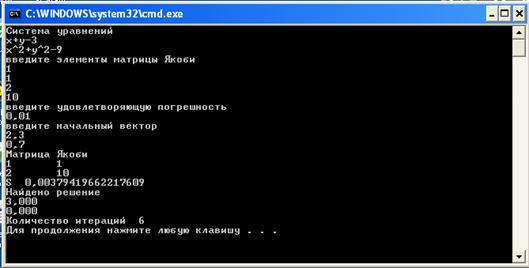
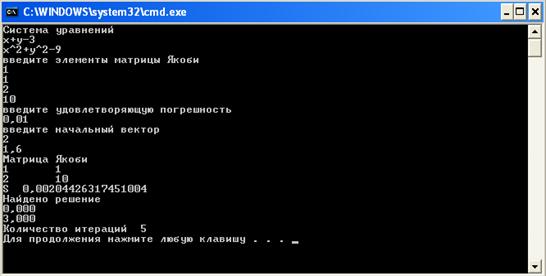
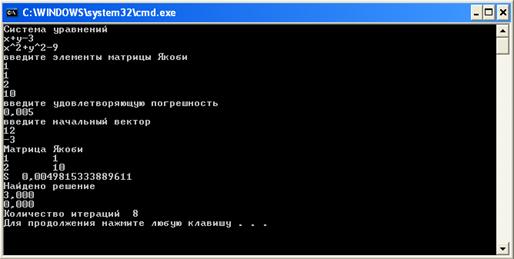
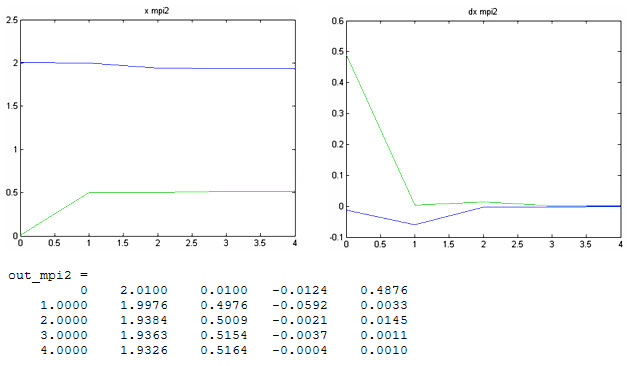
... 1040, мы все еще получаем сходимость, при количестве итераций порядка 130. 4 Анализ результатов, выводы Целью нашего исследование было сравнение методов простой итерации и Ньютона для решения систем из двух нелинейных уравнений по числу итераций, времени сходимости в зависимости от выбора начального приближения к решению и допустимой ошибки. Зависимость этих параметров от выбора начального ...
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...
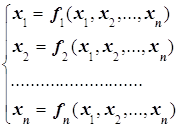
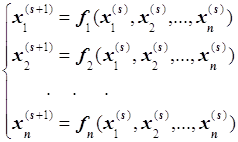
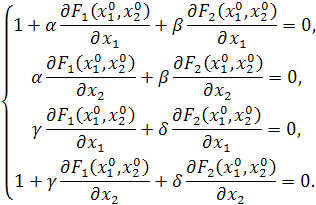



0 комментариев