Навигация
Модифицированный метод Ньютона
37732
знака
2
таблицы
12
изображений
3.4 Модифицированный метод Ньютона
Аналогично методу Ньютона построим матрицу Якоби для данной системы уравнений, выберем начальное приближение заведомо близко к решению, построим последовательность:
> with(LinearAlgebra):
> f1x:=diff(f1,x0);
> f1y:=diff(f1,y0);
> f1z:=diff(f1,z0);
> f2x:=diff(f2,x0);
> f2y:=diff(f2,y0);
> f2z:=diff(f2,z0);
> f3x:=diff(f3,x0);
> f3y:=diff(f3,y0);
> f3z:=diff(f3,z0);
> A:=<<f1x|f1y|f1z>,<f2x|f2y|f2z>,<f3x|f3y|f3z>>;
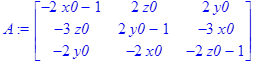
> x0:=0;y0:=0;z0:=0;
> A:=A;
> A1:=A^(-1);
> f:=<f1,f2,f3>;
> X0:=<x0,y0,z0>;
> X:=Add(X0,(Multiply(A1,f)),1,-1);
> X0:=X;
> x0:=X[1];y0:=X[2];z0:=X[3];
> f:=<f1,f2,f3>;
> i:=1;
> while (Norm(f))>0.0001 do
X0:=X;
x0:=X[1];y0:=X[2];z0:=X[3];
f:=<f1,f2,f3>;
X:=Add(X0,(Multiply(A1,f)),1,-1);
i:=i+1;
end do;
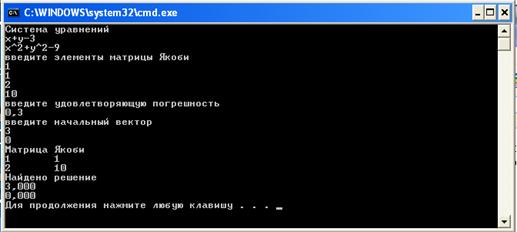
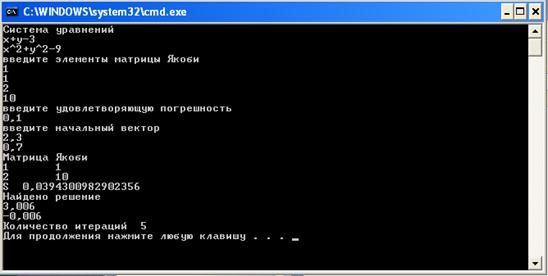
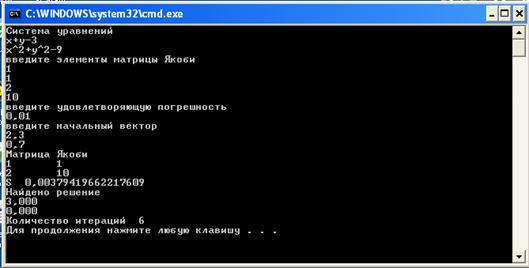
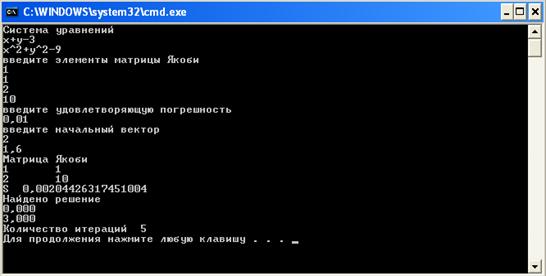
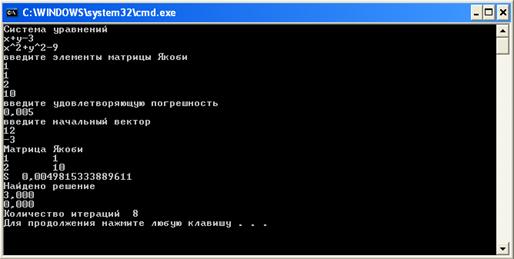
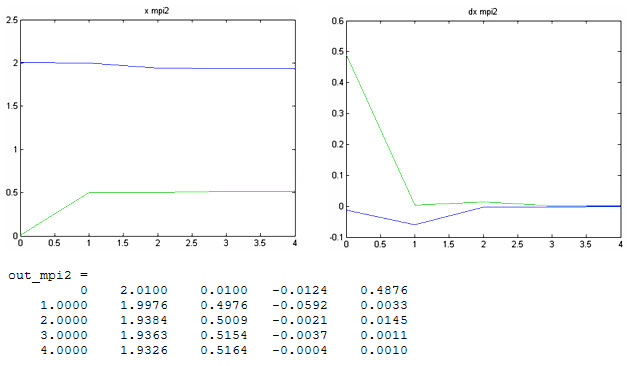
Получили ответ:
Количество итераций:
Текст программы
procedure TForm1.Button2Click(Sender: TObject);
type mas=array[1..3]of real;
matr=array[1..3,1..3]of real;
var x,y,z,ex,ey,ez,eps,b,c,d:real;
r,xk,f,temp:mas;
a,h,w,a1:matr;
i,kk: integer;
procedure jacobi(x,y,z:real; var a:matr);
procedure inverse(a:matr;var a1:matr);
procedure fx(x,y,z:real; var f:mas);
procedure minus(x,y:mas; var z:mas);
function max(f:mas):real;
procedure mult(a:matr;b:mas;var c:mas);
// все процедуры полностью совпадают с описанными выше реализации метода Ньютона
begin
xk[1]:=StrToFloat(Edit1.Text);
xk[2]:=StrToFloat(Edit2.Text);
xk[3]:=StrToFloat(Edit3.Text);
eps:=StrToFloat(Edit20.Text);
i:=0;
jacobi(xk[1],xk[2],xk[3],a);
inverse(a,a1);
repeat
fx(xk[1],xk[2],xk[3],f);
mult(a1,f,temp);
minus(xk,temp,xk);
i:=i+1;
until max(f)<eps;
Edit16.Text:=FloatToStr(xk[1]);
Edit17.Text:=FloatToStr(xk[2]);
Edit18.Text:=FloatToStr(xk[3]);
Edit19.Text:=IntToStr(i);
Выводы
Численное решение нелинейных алгебраических уравнений является сложной и не до конца разрешимой задачей вычислительной математики.
При решении систем нелинейных уравнений иногда поступают следующим образом. Строится функционал, минимум которого достигается в решении системы. Затем, задавши начальное приближение к точке минимума, проводят итерации каким-либо из методов спуска. И таким путём получают удовлетворительное приближение к решению системы. Исходя из этого приближения, проводят уточнения при помощи какого-либо итерационного метода, например метода Ньютона или Пикара.
Поясним причины, вызывающие такое комбинированное применение методов. Область сходимости метода – множество начальных условий, при которых итерации по данному методу сходятся к решению задачи. Применение методов спуска на первоначальном этапе вызвано тем, что они имеют более широкую область сходимости, чем методы специфические для задачи решения системы уравнений.
На нашем примере можно в этом убедиться.
Метод градиентного спуска при начальном приближении даже равном 
сходится к решению 
. При более отдалённом начальном приближении, например, 
приводит к другому решению (
) из множества решений системы. Как видим, полученные ответы значительно отличаются от первоначального приближения, что свидетельствует о широкой области сходимости метода градиентного спуска. Также заметим, что при разных удачно выбранных начальных приближениях этот метод может привести нас к любому решению системы уравнений. То есть, в построении метода нет привязки только к конкретному решению, он универсален. Однако скорость сходимости линейная, довольно медленная при выборе маленького шага. Поэтому и применяют этот метод первоначально, с относительно большим шагом и низкой точностью конечного решения для сокращения количества итераций при поиске приближения к корню, которое используют далее в других методах.
Метод Ньютона имеет высокую скорость сходимости, поэтому его удобнее применять, когда требуемая точность велика и известно приближённое значение решения. Однако область сходимости значительно уже.
Для метода простых итераций в нашем примере построено такое отображение, которое только при удачно выбранном начальном приближении к корню 
. При начальном приближении 
итерационная последовательность ещё сходится к решению, если взять начальные условия дальше от корня – метод не сходится ни к указанному выше, какому другому решению системы. Исходя из имеющихся данных про точное решение системы нелинейных уравнений, мы строим последовательность. Эта последовательность сходится только с начальным приближением лежащим в окрестности выбранного корня, и только к нему. Несмотря на возможную близость начального приближения к какому-то другому решению, она к нему не сойдётся, в отличие от других итерационных методов. Это говорит о том, что для каждого из множества решений системы нужно строить своё отображение, удовлетворяющее условиям сходимости. В этом проявляется недостаток метода простых итераций. Но если сжимающее отображение построено правильно, то преимущество метода состоит в простоте вычислений.
При модификации метода путём расчёта обратной матрицы Якоби только в начальной точке ведёт также к сужению области сходимости и к значительному увеличению количества итераций по мере выбора начального приближения дальше от точного решения.
Для решения систем нелинейных уравнений можно использовать метод Ньютона, метод простых итераций и др. Методы градиентного спуска и простой итерации имеют линейную сходимость, метод Ньютона - квадратичную, а квазиньютоновские – надлинейную скорость сходимости. Несмотря на то, что квазиньютоновские методы имеют худшую сравнительно с методом Ньютона теоретическую сходимость, они требуют при своей реализации меньшее количество машинных действий. Однако эти самые методы имеют локальную сходимости, то есть сходимость при хорошем начальном приближении. Для получения этого приближения во время решения систем нелинейных уравнений используют методы спуска и комбинируют их с методами, которые имеют большую скорость сходимости.
При применении того или иного метода к системе нелинейных уравнений нужно учитывать особенности постановки задачи и наличие начальных условий.
Список использованной литературы
1. Бахвалов Н.С., Лапин А.В., Чижонков Е.В. “Численные методы в задачах и упражнениях”. М.: Высшая школа, 2000.
2. Мышенков В.И., Мышенков Е.В., «Численные методы», учебное пособие,М., – 2001.
3. Амосов А.А., Дубинский Ю.А., Копченова Н.В. “Вычислительные методы для инженеров”. М.: Высшая школа, 1994.
4. Самарский А.А., Гулин А.В. «Численные методы».М.: Наука, 1989.
5. Назаренко Л.Д., «Численные методы», методическое пособие.
Похожие работы
... метод Бройдена, написана программа реализующая его. СПИСОК ЛИТЕРАТУРЫ 1. С.Л. Подвальный, Л.В. Холопкина. Вычислительная математика- учебное пособие ВГТУ, 2004 - 147 с. 2. Методы решения систем нелинейных уравнений. Метод Ньютона. Его реализации и модификации. - Электрон. дан. – Режим доступа: www.exponenta.ru/educat/referat/XVkonkurs/15/index.asp. ПРИЛОЖЕНИЕ Текст программы ...
... –0.6 = 0 9. 10. ( x -1)3 + 0.5ex = 0 11. 12. x5 –3x2 + 1 = 0 13. x3 –4x2 –10x –10 = 0 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. x 4- 2.9x3 +0.1x2 + 5.8x - 4.2=0 25. x4+2.83x3- 4.5x2-64x-20=0 26. МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 1. Постановка задачи Пусть требуется решить систему n ...
... 1040, мы все еще получаем сходимость, при количестве итераций порядка 130. 4 Анализ результатов, выводы Целью нашего исследование было сравнение методов простой итерации и Ньютона для решения систем из двух нелинейных уравнений по числу итераций, времени сходимости в зависимости от выбора начального приближения к решению и допустимой ошибки. Зависимость этих параметров от выбора начального ...
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...
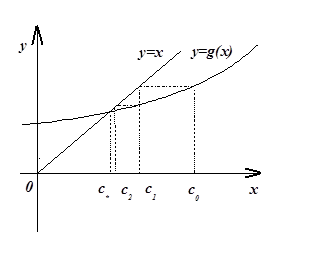
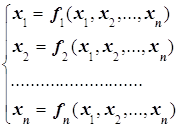
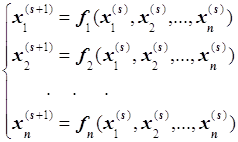
0 комментариев