Навигация
Приведение произвольного преобразования к нормальной форме
2. Приведение произвольного преобразования к нормальной форме
Уже упоминалось в п. 1, что в случае, когда у преобразования А не хватает линейно независимых собственных векторов (т. е. когда их число меньше размерности пространства), базис приходится дополнять за счет так называемых присоединенных векторов (их точное определение будет дано чуть позже). В этом разделе дается способ построения базиса, в котором матрица преобразования А имеет жорданову нормальную форму. Этот базис мы непосредственно наберем из собственных и присоединенных векторов, и такой способ выбора является , в некотором смысле. Наиболее естественным.
2.1 Собственные и присоединенные векторы линейного преобразования
Пусть l0 – некоторое собственное значение преобразования А.
Определение 1. Вектор х ¹ 0 называется собственным вектором преобразования А, отвечающим собственному значению l0, если
Ах = l0х, т. е. (А - l0Е)х = 0. (1)
Рассмотрим совокупность всех векторов, удовлетворяющих условию (1) при фиксированном l0. Ясно, что совокупность этих векторов является подпространством пространства R
Обозначим его ![]() . Легко видеть, что
. Легко видеть, что ![]() инвариантно относительно преобразования А.
инвариантно относительно преобразования А.
Заметим, что подпространство ![]() состоит из всех собственных векторов преобразования А, отвечающих собственному значению l0, к которым добавлен еще нулевой вектор.
состоит из всех собственных векторов преобразования А, отвечающих собственному значению l0, к которым добавлен еще нулевой вектор.
Определение 2. Вектор х называется присоединенным вектором 1-го порядка преобразования А, отвечающим собственному значению l0, если вектор
у = (А - l0Е)х
является собственным вектором преобразования А.
Пусть l0 – собственное значение преобразования А.
Подпространство, состоящее из всех векторов х, для которых выполнено условие
(А - l0Е)2х = 0, (2)
т. е. ядро преобразования (А - l0Е)2 , обозначим ![]() .
. ![]() является инвариантным подпространством пространства R. А получается это подпространство, если к подпространству
является инвариантным подпространством пространства R. А получается это подпространство, если к подпространству ![]() добавить присоединенные векторы 1-го порядка.
добавить присоединенные векторы 1-го порядка.
Аналогично вводим подпространство ![]() , состоящее из всех векторов х, для которых
, состоящее из всех векторов х, для которых
(А - l0Е)kх = 0. (3)
Это подпространство инвариантно относительно преобразования А. Ясно, что подпространство ![]() содержит предыдущее подпространство
содержит предыдущее подпространство ![]() .Определение 3. Вектор х называется присоединенным вектором k-го порядка, если вектор
.Определение 3. Вектор х называется присоединенным вектором k-го порядка, если вектор
у = (А - l0Е)х
есть присоединенный вектор порядка k-1.
Пример. Пусть R – пространство многочленов степени £ n-1 и преобразование А – дифференцирование:
АР(t) = ![]() P(t).
P(t).
Легко видеть, что l = 0 есть собственное значение. Соответствующий ему собственный вектор P(t) = const. Найдем для этого преобразования подпространства ![]() . По определению
. По определению ![]() состоит из всех многочленов P(t), для которых АkР(t) = 0, т. е.
состоит из всех многочленов P(t), для которых АkР(t) = 0, т. е.
![]()
Это будут все многочлены, степень которых не превышает k-1. Присоединенными векторами k-го порядка будут многочлены, степень которых в точности равна k-1.
2.2 Выделение подпространства, в котором преобразование А имеет только одно собственное значение
Пусть l1 – некоторое собственное значение преобразования А. Пространство R можно разложить в прямую сумму двух инвариантных подпространств, в первом из которых преобразование А имеет лишь одно собственное значение l1, а во втором у преобразования А уже нет собственного значения l1.
Не ограничивая общности, можно считать, что l1 = 0.
Действительно, пусть l1 ¹ 0. Рассмотрим преобразование В = А - l1Е; оно уже имеет собственное значение, равное нулю. Очевидно также, что инвариантные подпространства преобразований А и В совпадают.
Итак, будем считать, что преобразование А имеет собственное значение l= 0. Докажем это утверждение сначала для частного случая, когда в пространстве нет присоединенных векторов, отвечающих этому собственному значению, а есть только собственные векторы.
Нам нужно построить два инвариантных подпространства, прямая сумма которых равна R. В качестве первого из них, в котором l= 0 есть единственное собственное значение, можно взять совокупность N0 всех собственных векторов, отвечающих собственному значению l= 0 или, другими словами, ядро преобразования А.
В качестве второго подпространства возьмем образ М пространства R при преобразовании А, т. е. совокупность векторов у = Ах, где х пробегает все пространство R. Легко видеть, что каждое из этих подпространств инвариантно.
Они дают разложение пространства в прямую сумму. Так как сумма размерностей ядра и образа для любого преобразования А равна n, то достаточно доказать, что пересечение этих подпространств равно нулю.
Предположим, что это не так, т. е. пусть существует вектор у ¹ 0 такой, что уÎМ и уÎN0. Так как уÎМ, то он имеет вид
у = Ах, (4)
где х – некоторый вектор из R. Так как уÎN0, то
Ау = 0, где у ¹ 0. (5)
Равенство (5) означает, что у есть собственный вектор преобразования А, отвечающий собственному значению l= 0, а равенство (4) при этом означает, что х есть присоединенный вектор первого порядка, отвечающий тому же собственному значению. Мы же предположили, что у преобразования А нет присоединенных векторов, отвечающих собственному значению l= 0.
Таким образом доказано, что подпространства М и N0 не имеют общих векторов кроме нулевого.
Вспоминая, что сумма размерностей образа и ядра равна n, мы получаем отсюда, что пространство R разложимо в прямую сумму инвариантных подпространств М и N0:
R = M + N0.
Замечание. Из приведенного выше доказательства видно, что образ и ядро имеют пересечение, отличное от нуля в том и только случае, когда преобразование А имеет присоединенные векторы, отвечающие собственному значению l= 0.
Разобранный частный случай дает нам идею того, как проводить доказательство в общем случае, когда А имеет также и присоединенные векторы, отвечающие собственному значению l= 0. Подпространство N0 при этом оказывается слишком узким, и его естественно расширить за счет добавления всех присоединенных векторов, отвечающие собственному значению l= 0. Второе же подпространство М оказывается при этом слишком большим.
Теорема. Пространство R можно разложить в прямую сумму инвариантных подпространств ![]() и
и ![]() . При этом подпространство
. При этом подпространство ![]() состоит только из собственных и присоединенных векторов, отвечающих собственному значению l= 0, а в подпространстве
состоит только из собственных и присоединенных векторов, отвечающих собственному значению l= 0, а в подпространстве ![]() преобразование А обратимо ( т. е. l= 0 не является собственным значением преобразования А в подпространстве
преобразование А обратимо ( т. е. l= 0 не является собственным значением преобразования А в подпространстве ![]() ).
).
Если l1 – некоторое собственное значение преобразования А, то пространство R можно разложить в прямую сумму инвариантных подпространств R1 и ![]() , в первом из которых преобразование А имеет только собственное значение l1, а во втором все собственные значения А отличны от l1.
, в первом из которых преобразование А имеет только собственное значение l1, а во втором все собственные значения А отличны от l1.
Применяя полученный результат к преобразованию А в пространстве ![]() и к некоторому собственному значению l2 этого преобразования, мы «отщепим» инвариантное подпространство, отвечающее собственному значению l2. Продолжая этот процесс, пока не будут исчерпаны все собственные значения преобразования А, мы получим доказательство следующей теоремы:
и к некоторому собственному значению l2 этого преобразования, мы «отщепим» инвариантное подпространство, отвечающее собственному значению l2. Продолжая этот процесс, пока не будут исчерпаны все собственные значения преобразования А, мы получим доказательство следующей теоремы:
Теорема. Пусть преобразование А пространства R имеет k различных собственных значений l1, … , lk.. Тогда R можно разложить в прямую сумму k инвариантных подпространств ![]() , …,
, …, ![]() :
:
R = ![]() + … +
+ … + ![]() . (6)
. (6)
Каждое из подпространств ![]() состоит только из собственных и присоединенных векторов, отвечающих собственному значению li.
состоит только из собственных и присоединенных векторов, отвечающих собственному значению li.
Осталось еще только одна не менее важная задача – выбрать в каждом из этих подпространств базис, в котором матрица преобразования имеет жорданову нормальную форму.
Похожие работы
... понятия собственного числа линейного оператора А. 120. Определите, каким является базис а=(1/, 1/,1/), b=(1/, -1/, 0), с =(1/, 1/,-2/). Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЛИНЕЙНАЯ АЛГЕБРА Билет № 26 121. Приведение матрицы к ступенчатому виду методом Гаусса. Пример. 122. ...
... его за прямые скобки. Оставшиеся коэффициенты упорядочены, как в матрице . Теперь для представления исходной системы уравнений в виде несложно определить векторно-матричную операцию , результатом которой является вектор с i-той компонентой, равной . Аксиоматическое построение линейной (векторной) алгебры с рассмотренными базовыми операциями позволило установить важные и полезные свойства, как ...
... (3.3) известен. Он состоит из компонент и имеет единичный базис Б = = E. Решая вспомогательную задачу первым алгоритмом симплекс-метода (описание алгоритма приводится в п.4), в силу ограниченности линейной формы сверху на множестве своих планов () получим, что процесс решения через конечное число шагов приведет к оптимальному опорному плану вспомогательной задачи. Пусть - оптимальный опорный ...
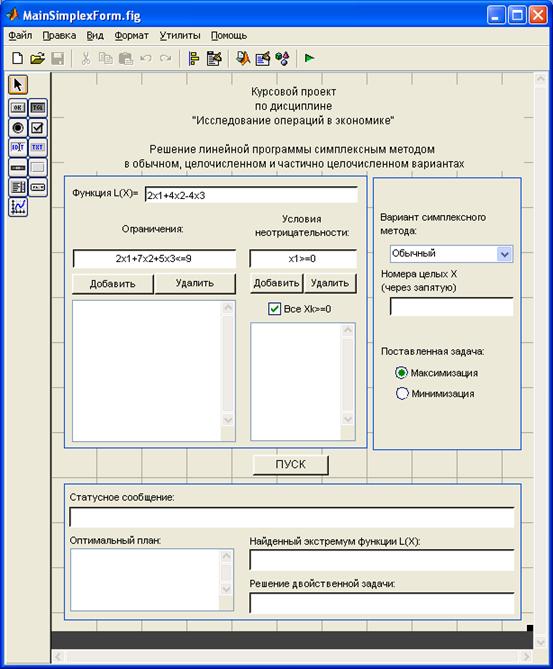
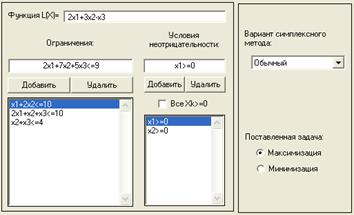
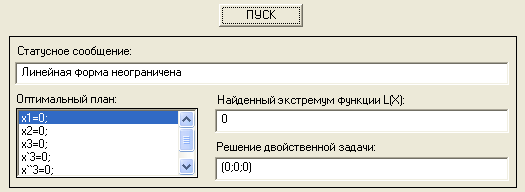
... на встроенном языке среды MatLAB, позволяющее решать линейные программы симплексным методом с учетом приведенного выше теоретического материала. Несмотря на то, что в поставляемом вместе с MatLAB пакете программ Optimization Toolbox имелась функция linprog реализующая решение линейных задач, было принято решение реализовывать симплекс-метод и метод Гомори не используя уже готовые решения, но ...

0 комментариев