Навигация
1. Дистрибутивность.
Отображения: ![]() и
и ![]() согласованы на идеале
согласованы на идеале ![]() покажем, что образы отображений
покажем, что образы отображений ![]() и
и ![]() совпадают на этом идеале:
совпадают на этом идеале:
пусть ![]() , где
, где ![]() .
.
Тогда ![]() .
.
Областью определения ![]() является
является ![]() . По определению идеала:
. По определению идеала: ![]() то
то ![]() для
для ![]() , а идеал
, а идеал ![]() (свойство 30) то:
(свойство 30) то: ![]() . Тогда по определению сложения
. Тогда по определению сложения ![]() отсюда следует
отсюда следует ![]() . Покажем
. Покажем ![]() . По определению
. По определению 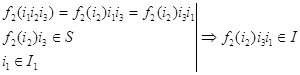
Аналогично ![]() .
.
Тогда:
![]() Таким образом,
Таким образом, ![]() где
где ![]() . По свойству 30
. По свойству 30![]() - плотный идеал значит
- плотный идеал значит ![]() и
и ![]() согласованы на плотном идеале
согласованы на плотном идеале ![]()
![]()
![]() .
.
2. Коммутативность.
Отображения ![]() и
и ![]() согласованы на плотном идеале
согласованы на плотном идеале ![]() докажем что их образы совпадают на этом идеале:
докажем что их образы совпадают на этом идеале: ![]() .
.
Доказано ранее, что 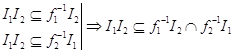 пусть элементы
пусть элементы ![]() тогда
тогда ![]()
Отсюда следует, что ![]() и
и ![]() согласованы на плотном идеале
согласованы на плотном идеале ![]() .
.
Таким образом, ![]() по Лемме 1.
по Лемме 1.
Наконец ![]() сопоставим дробь:
сопоставим дробь: ![]() с областью определения
с областью определения ![]() при которой
при которой ![]() переходит в
переходит в ![]() .
.
Предложение2. Отображение ![]() является гомоморфизмом т.е. сохраняет операции:
является гомоморфизмом т.е. сохраняет операции:
![]()
![]()
Доказательство:
1. Пусть ![]() ,
, ![]() и
и ![]() где
где ![]() и
и ![]() .
.
Нужно показать, что ![]() . Покажем равенство образов
. Покажем равенство образов ![]() и
и ![]() .
.
Рассмотрим дробь ![]() , такую что
, такую что
![]() для
для ![]() . (1)
. (1)
С другой стороны рассмотрим дроби ![]() и
и ![]()
![]() , такие что
, такие что ![]() для
для ![]() . (2)
. (2)
Из (1) и (2) следует, что ![]() .
.
По свойству сложения смежных классов:
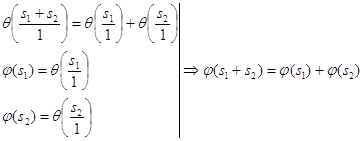 для
для ![]()
2. Пусть ![]() ,
, ![]() и
и ![]() где
где ![]() и
и ![]() .
.
Нужно показать, что ![]() . Покажем равенство образов
. Покажем равенство образов ![]() и
и ![]() .
.
Рассмотрим дробь ![]() , такую что
, такую что
![]() для
для ![]() . (3)
. (3)
С другой стороны рассмотрим дроби ![]() и
и ![]()
![]() , такие что
, такие что ![]() для
для ![]() . (4)
. (4)
Из (3) и (4) следует, что ![]() .
.
По свойству умножения смежных классов:
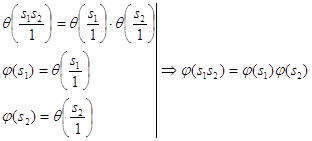 для
для ![]() .
.
Таким образом ![]() гомоморфизм.
гомоморфизм.
Пусть ![]() , тогда
, тогда
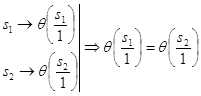 т.е.
т.е. ![]() и
и ![]() согласованы на некотором плотном идеале
согласованы на некотором плотном идеале ![]() значит
значит ![]() для
для ![]() , так как
, так как ![]() - плотный идеал, то
- плотный идеал, то ![]() отсюда
отсюда ![]() - инъективно.
- инъективно.
Поэтому, гомоморфизм ![]() является мономорфизмом и
является мономорфизмом и ![]() вкладывается в полное полукольцо частных.
вкладывается в полное полукольцо частных.
Гомоморфизм ![]() будем называть каноническим мономорфизмом
будем называть каноническим мономорфизмом ![]() в
в ![]() .▲
.▲
Глава 3.
Определение5.Любому мультипликативно сокращаемому элементу ![]() сопоставим плотный идеал
сопоставим плотный идеал ![]() . Если
. Если ![]() , то элемент
, то элемент ![]() назовём классической дробью, полагая
назовём классической дробью, полагая ![]() для
для ![]() .
.
Теорема3. Множество дробей ![]() образует подполукольцо полного полукольца частных, изоморфное классическому полукольцу частных
образует подполукольцо полного полукольца частных, изоморфное классическому полукольцу частных ![]() полукольца
полукольца ![]() .
.
Доказательство:
Рассмотрим отображение ![]() , т.е.
, т.е. ![]() .
.
1. Докажем, что ![]() - отображение: если
- отображение: если ![]() и
и ![]() ,
, ![]() , где
, где ![]() ,
, ![]() , то
, то ![]() .
.
Имеем ![]()
Возьмём элемент ![]() из пересечения плотных идеалов
из пересечения плотных идеалов ![]() , т.е.
, т.е. ![]() и
и ![]()
Тогда 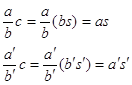 , домножим
, домножим ![]() на
на ![]() получим
получим ![]() . Так как
. Так как ![]() и на
и на ![]() выполняется коммутативность по умножению, то
выполняется коммутативность по умножению, то ![]() ,
, ![]() отсюда
отсюда ![]() для
для ![]()
![]() .
.
2. Докажем, что ![]() является полукольцевым гомоморфизмом, т.е. сохраняются полукольцевые операции.
является полукольцевым гомоморфизмом, т.е. сохраняются полукольцевые операции.
2.1
![]()
![]()
![]() . Покажем, что дробь
. Покажем, что дробь ![]() согласована с
согласована с ![]() на плотном идеале
на плотном идеале ![]() .
.
Пусть ![]() ,
, ![]() .
.
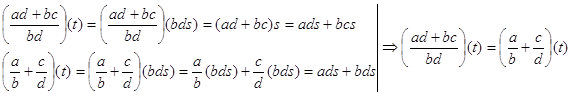
для ![]() .
.
Следовательно ![]() .
.
2.2
![]()
![]() .
.
Идеал ![]() содержит
содержит ![]() , покажем, что
, покажем, что ![]() и
и ![]() согласованы на плотном идеале
согласованы на плотном идеале ![]() .
.
Пусть ![]() ,
, ![]() . Тогда
. Тогда
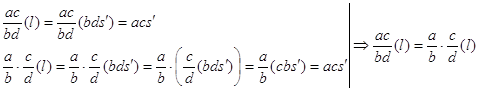 для
для ![]() .
.
Значит ![]() .
.
Таким образом ![]() - полукольцевой гомоморфизм классического полукольца частных
- полукольцевой гомоморфизм классического полукольца частных ![]() в полное полукольцо частных
в полное полукольцо частных ![]() .
.
3. Докажем, что ![]() - инъективный гомоморфизм.
- инъективный гомоморфизм.
Пусть для ![]() . Предположим, что дроби
. Предположим, что дроби ![]() и
и ![]() согласованы на некотором плотном идеале
согласованы на некотором плотном идеале ![]() , т.е. для
, т.е. для ![]() выполнено
выполнено ![]() . Но
. Но ![]() ,
, ![]() . Тогда
. Тогда 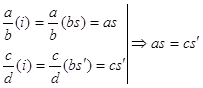 . Домножим обе части равенства на
. Домножим обе части равенства на ![]() получим:
получим:
![]() т.к.
т.к. ![]() - плотный идеал
- плотный идеал ![]() , что противоречит условию.
, что противоречит условию.
Значит, ![]() является инъективным гомоморфизмом или мономорфизмом
является инъективным гомоморфизмом или мономорфизмом ![]() в
в ![]() .
.
Так как ![]() , то
, то ![]() , где
, где ![]() - элемент подполукольца полного полукольца частных
- элемент подполукольца полного полукольца частных ![]() , т.е.
, т.е. ![]() и
и ![]() . Поскольку
. Поскольку ![]() - инъективный гомоморфизм, то по теореме о гомоморфизме существует изоморфизм
- инъективный гомоморфизм, то по теореме о гомоморфизме существует изоморфизм ![]() отсюда следует
отсюда следует ![]() .
.
Мономорфизм ![]() называется вложением классического полукольца частных
называется вложением классического полукольца частных ![]() в полное полукольцо частных
в полное полукольцо частных ![]() полукольца
полукольца ![]() .▲
.▲
Библиографический список
1. Вечтомов, Е. М. Введение в полукольца [Текст] / Е. М. Вечтомов. – Киров.: ВГПУ, 2000.
2. Ламбек, И. Кольца и модули [Текст] / И. Ламбек. – Москва.: Мир, 1971. – 288 с.
3. Чермных, В. В. Полукольца [Текст] / В. В. Чермных. – Киров.: ВГПУ, 1997. – 131 с.
Похожие работы
... ; 3. Идеал на полукольце : ; 4. Главный идеал ограниченной дистрибутивной решетки L, порожденный элементом a: . Глава II «Положительные и ограниченные полукольца». 2.1. Определение, примеры и основные свойства. Полукольцо S с 1 называется положительным, если для любого элемента а S элемент а+1 обратим в S, т.е.. Примерами положительных полуколец служат следующие алгебраические системы: ...
... S с 1 изоморфно прямому произведению кольца и антикольца тогда и только тогда, когда его идеал R(S) имеет единичный элемент, коммутирующий с каждым элементом из S [1]. 3. Полукольцо S служит 0-расширением кольца с помощью полутела тогда и только тогда, когда идеал R(S) полульца S простой (т.е. abÎR(S) влечет aÎR(S) или bÎR(S)). 4. Для полукольца S с 1 фактор-полукольцо S/R(S) ...
... передает здесь идею целой структуры, а не какого-то ее элемента, взаимодействующего с другими"60. Само наличие антропоморфных изваяний безусловно наносит сильный удар концепции исключительно зооморфного характера мировоззрения скифов на ранних этапах их истории. А, как пишет Раевский, "практическая одновременность появлений рассмотренных изображений и древнейших памятников звериного стиля ...
... Расстановку оборудования по цехам и производствам осуществляют методом плоскостного моделирования на планах производственных цехов в масштабе 1:100. 3. ТЕХНОЛОГИЧЕСКИЕ РАСЧЕТЫ КОЛБАСНОГО ЦЕХА. 3.1. Расчет сырья и материалов. Расчеты сырья колбасных мини-цехов и цехов мясокомбинатов различны и могут быть условно разделены на следующие группы: расчет цеха убоя скота и разделки туш; расчет ...





0 комментариев