Навигация
Положительные и ограниченные полукольца
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет
Математический факультет
Кафедра алгебры и геометрии
Выпускная квалификационная работа
Положительные и ограниченные полукольца
Выполнил:
студент V курса математического факультета
Ворожцов Вячеслав Андреевич _____
Научный руководитель:
кандидат физико-математических наук, доцент кафедры алгебры и геометрии В.В. Чермных ________
Рецензент:
доктор физико-математических наук, профессор кафедры алгебры и геометрии Е.М. Вечтомов _______
Допущена к защите в государственной аттестационной комиссии
«___» __________2005 г. Зав. кафедрой Е.М. Вечтомов
«___»___________2005 г. Декан факультета В.И. Варанкина
Киров
2005
Содержание
Введение........................................................................................................... 3
Глава 1. Основные понятия теории полуколец ............................................. 4
1.1. Определение полукольца. Примеры.................................................. 4
1.2. Дистрибутивные решетки.................................................................... 5
1.3. Идеалы полуколец............................................................................... 6
Глава 2 Положительные и ограниченные полукольца.................................. 7
2.1. Определение и примеры положительных и ограниченных полуколец 7
2.2. Основные свойства положительных и ограниченных полуколец..... 7
Библиографический список........................................................................... 16
Введение
Теория полуколец – это раздел современной алгебры, обобщающий как кольца, так и дистрибутивные решетки. Понятие полукольца возникло в 30-х годах прошлого столетия. Как самостоятельная теория полукольца начали изучаться в 50-е годы. Особенно интенсивно теория полуколец развивается последние 20 лет, что вызвано не только теоретическим интересом, но и многочисленными ее приложениями.
Целью данной работы является изучение классов положительных и ограниченных полуколец, рассмотрение основных свойств данных алгебраических объектов, часть из которых доказывается автором работы самостоятельно; приведены примеры полуколец.
Работа состоит из 2 глав. В первую главу вошли основные определения и факты, на которые опирается эта работа. Вторая – основная часть всей работы, в ней рассмотрены определения и свойства положительных и ограниченных полуколец, приведены примеры, доказаны некоторые теоремы.
Глава I. «Основные понятия теории полуколец».
1.1. Определение полукольца. Примеры.
Определение полукольца: Непустое множество S с бинарными операциями + и · называется полукольцом, если выполняются следующие аксиомы:
1. (S,+) – коммутативная полугруппа с нейтральным элементом 0;
· Ассоциативность: ![]() ;
;
· Коммутативность: ![]() ;
;
· Существование нейтрального элемента: ![]() .
.
2. (S,·) – полугруппа:
· Ассоциативность: ![]() ;
;
3. Умножение дистрибутивно относительно сложения:
· левая дистрибутивность: ![]() а(в+с)=ав+ас;
а(в+с)=ав+ас;
· правая дистрибутивность: ![]() (а+в)с=ас+вс.
(а+в)с=ас+вс.
4. Мультипликативное свойство 0:
· ![]() .
.
Эта аксиоматика появилась в 1934 году и ее автором является Вандовер.
Полукольцо S называется коммутативным, если операция ![]() в нем коммутативна:
в нем коммутативна: ![]() .
.
Полукольцо S называется полукольцом с единицей, если в нем существует нейтральный элемент по умножению, который называется единицей (1): ![]()
Примеры полуколец:
1. <N,+,·>, где N – множество неотрицательных целых чисел с обычными операциями + и ·;
2. <{0},+,·> - тривиальное полукольцо;
3. Двухэлементные полукольца:<Z2 ,+,·>, <В,+,·> (в В 1+1=1);
4. Множество матриц ![]() с элементами из полукольца N и операциями + и
с элементами из полукольца N и операциями + и ![]() ;
;
5. Множества N, Z, Q+, Q, R+, R и введенных на них различных комбинаций операций: обычные сложение и умножение, максимум ![]() и минимум
и минимум ![]() двух чисел, НОД и НОК, когда они определены.
двух чисел, НОД и НОК, когда они определены.
Полукольцо с импликацией ![]()
![]() называется мультипликативно (аддитивно) сократимым.
называется мультипликативно (аддитивно) сократимым.
Полукольцо, в котором выполняется равенство ![]()
![]() , называется мультипликативно (аддитивно) идемпотентным.
, называется мультипликативно (аддитивно) идемпотентным.
Похожие работы
... S с 1 изоморфно прямому произведению кольца и антикольца тогда и только тогда, когда его идеал R(S) имеет единичный элемент, коммутирующий с каждым элементом из S [1]. 3. Полукольцо S служит 0-расширением кольца с помощью полутела тогда и только тогда, когда идеал R(S) полульца S простой (т.е. abÎR(S) влечет aÎR(S) или bÎR(S)). 4. Для полукольца S с 1 фактор-полукольцо S/R(S) ...
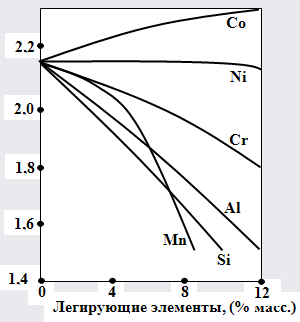
... Фк = 365 × 24 = 8760 ч Номинальный фонд времени – это количество часов в году в соответствии с режимом работы без учета потерь. Так как термическое отделение высокотемпературного отжига анизотропной электротехнической стали работает непрерывно, то номинальный фонд равен полному календарному, то есть Фн = Фк = 8760 ч. Действительный фонд времени равен тому времени, которое может быть ...
... дела как нельзя лучше играла на руку вредителям». (Мордвинов А.Г. «Искусство в массы», 1930, №12. От редакции «Современная архитектура», 1930, №5, стр. 2—3). 4. Коммуна и человек. Жилые дома и клубы Теперь перейдем к конкретным постройкам в Москве 1920-х годов. В первую очередь надо было решать жилищную проблему. Жилищное строительство после нескольких лет разрухи и гражданской войны ...
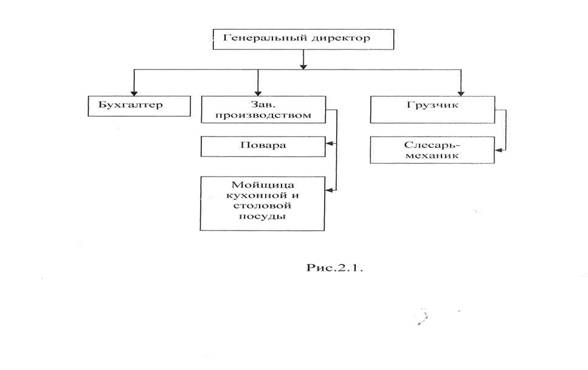
... и отпуска холодных блюд 10-14С; - повар обязательно следит за чистотой своего места. Отходы собираются в специальный отдельный бак и выносятся два раза в день. 3.4 Организация работы овощного цеха В столовой овощной цех находится рядом с кладовой овощей. Овощные полуфабрикаты поступают в горячий и холодный цеха, где и завершается выпуск готовой продукции. Технологический процесс ...
0 комментариев