Навигация
Розділ I. Елементи теорії множин
§1.1. Поняття множини
Поняття множини є одним з фундаментальних у математиці. Воно належить до понять яким не можна дати строге означення, тобто до так званих первісних, які не можна визначити через простіші поняття. Інтуєтивно множину розуміють як сукупність (сімейство, набір, зібрання, клас) деяких, обєктів об’єднаних за певною ознакою чи властивістю. Наприклад; множина студентів першого курсу, сукупність тих із них, які здали вступні екзамени без трійок і сімейство зірок Великої Ведмедиці, система трьох рівнянь з 3-ма невідомими, множина цілих чисел.
Об’єкти, із яких складається множина, називаються її елементами. Множини позначається великими буквами, а її елементи малими. Те, що елемент а належить множені А записується так а ![]() А. Запис а
А. Запис а ![]() є А або а
є А або а ![]() А означає, що елемент а не належить множені А.
А означає, що елемент а не належить множені А.
Окремі найважливіші множини мають загальноприйняте позначення
· N – множина натуральних чесел (1, 2, 3, 4…)
· Z – множина цілих чисел (…-3, -2, -1, 0, 1, 2, 3…)
· Q – множина раціональних чисел (Z + дробові числа)
· I – множина всіх ірраціональних чисел
· R – множина дійсних чисел ( Q + ірраціональні чисела)
Множина, що містить безліч елементів називається нескінченною. Приклад: множина усіх точок даного відрізку, що проходить через задану точку, множина усіх прямих паралельних заданій прямій.
Множина, яка містить скінчену кількість елементів називається скінченою.
Запис A={a1, a2, a3… an} означає, що множина А скінчена і містить n елементів. Множина Х={x1, x2… , xn….} – є незкінченою. Множина, яка не містить жодного елементу називаєтся порожньою і позначається символом ![]() .
.
Приклади: Множина дійсних коренів рівняння x2+1=0, множина усіх цілих чисел, що діляться на 4, але не діляться на 2.
Нехай P(x) – деяка властивість (закон, правило, форма) числа х, тоді запис
{x| P(x)} означає множину всіх тих чисел х, для яких виконується властивість Р(х). Наприклад:
1. {x|x є R, x2 + 3x + 4 =0} множина тих дійсних чисел х, які є розв’язками рівняння x2 + 3x + 4 =0.
2. А={x| x є z, |x|≤100} – множина тих цілих чисел модуль яких не більший за 100, тобто елеменетами множини А є цілі числа по порядку від -100 до +100.
Множину можна подати у вигляді відрізку на числовій осі:
![]() x
x
-3 -2 -1 0 1 2 3 4 5 6
мал.1.1
А={x| x є R, 2 ≤ x < 5} A=[2,5)
Числові проміжки позначаються так:
Нехай а і b – дійсні числа, причому а<b.
Розглянемо числові множини.
· [a; b] = {x|a ≤ x ≤ b } – закритий відрізок, сегмент;
· (a; b) = {x|a < x < b } – відкритий інтервал;
· (a; b] = {x|a < x ≤ b } – напівінтервал, напіввідкритий інтервал,
· [a; b) = {x|a ≤ x < b } – напівсегмент;
· (- ∞; + ∞) = {x|- ∞ < x < + ∞ } – нескінченно відкритий інтервал.
Введемо інтервал, що називається околом точки. Нехай х0 – довільне дійсне число. Околом точки х0 називається будь-який інтервал (α; β), що містить цю точку, тобто α < x0 < β. Так околом точки x0 = 1 є інтервал ( - 0,5; 1,5), (0,2) і т. д.
Інтервал (x0 – Е, x0 + Е ), де Е > 0 називається Е – околом точки х0, при цьому точку х0 називають центром, а число Е – радіусом околу. Цей окіл буде досить малий, якщо число Е теж буде мале.
Нехай задано дві множини А і В. Якщо кожен елемент множини А є елементом мнгожини В, то множину А називають підмножиною множини В і пишуть А![]() В (А міститься в В).
В (А міститься в В).
Наприклад N ![]() Z. Очевидно, що кожна множина є своєю підмножиною, а порожня множина є підмножиною будьякої множини.
Z. Очевидно, що кожна множина є своєю підмножиною, а порожня множина є підмножиною будьякої множини.
Якщо множини А і В містять одні і ті ж елементи, тобто А![]() В і В
В і В![]() А, то їх називають рівними і пишуть А=В.
А, то їх називають рівними і пишуть А=В.
Множину, різні підмножини якої доводиться розглядати в процесі вивчення якогось питання, називають універсальною множиною.
У поцесі вивчення множин і функцій бувають корисними певні графічні зображення. У випадку множин застосовується діаграми Ейлера-Венна. На цих діаграмах схематично зображається універсальна множина у вигляді прямокутника, а різні підмножини універсальної множини у вигляді кругів.(мал.1.2).
А не має спільних елементів з В і С , а В і С мають спільні елементи.
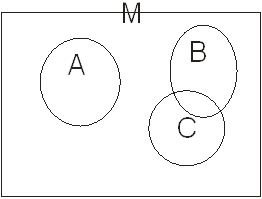
мал.1.2
§1. 2 Операції над множинами. Об’єднання і переріз двох множин.
Об’єданням двох множин А і В, називається множина А U В, елементи якої належать хочаб одній із цих множин.(мал.1.3)
![]()
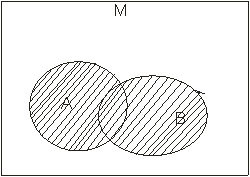
мал.1.3
Об’єдання декількох множин.
![]() Ai= A1 U A2 U A3 U…U An
Ai= A1 U A2 U A3 U…U An
![]() Ai={x | x є А1 або х є А2 або х є А3 або …х є Аn}
Ai={x | x є А1 або х є А2 або х є А3 або …х є Аn}
Перерізом двох множин А і В називається множина А ∩ В елементи якої належать як і множині А, так і множені В. (мал.1.4)
А ∩ В={x | х є А і х є В}
![]() Ai={x | x є А1 і х є А2, х є А3…х є Аn}
Ai={x | x є А1 і х є А2, х є А3…х є Аn}
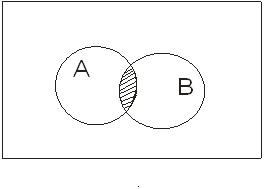
мал.1.4
Властивості об’єдання і перерізу множин:
1. Комутативний (переставний) закон
А U B = В U А;
А ∩ В = В ∩ А;
2. Асоціативний (сполyчний) закон.
А ∩ (В ∩ С) = (А ∩ В) ∩ С
А U (В U С) = (А U B) U С
3. Дистрибутивний (розподільний) закон.
А U (В ∩ С)=(А U B) ∩ (А U С)
А ∩ (В U С)=(А ∩ В) U (А ∩ С)
4. А U Ø = А.
5. А ∩ Ø = Ø.
Ці закони легко довести за допомогою діаграм. Доведемо 3-й дистрибутивний закон:
А U (В ![]() С) = (А U B) ∩ (А U С)
С) = (А U B) ∩ (А U С)

А U (В U С) (А U B) ∩ (А U С)
мал.1.5 мал.1.6
А ∩ (В U С)=(А ∩ В) U (А ∩ С)

А ∩ (В U С) (А ∩ В) U (А ∩ С)
мал.1.7 мал.1.8
§1. 3 Різниця і доповненя множин.
На відміну від об’єднання і перізу множин, операція віднімання визначається лише для двох множин якщо вони перетенаються.
Різницею множин А та В називається множина А\В, яка складається зусіх тих елементів, які належать множині А і не належать В.(мал.1.9)

А \ В = {x | x є A I x ¢ B}
мал.1.9
![]() Властивості різниці :
Властивості різниці :
· А \ В ≠ В \ А – не комутативна .
· А \ (В \ С) ≠ (А \ В) \ С – не асоціативна
· А U Ø = А.
· А ∩ Ø = Ø.
· (B U C) \ A=(B \ A) U (C \ A) – дисрибутивний закон віднімання відносно об’єдання;
· (B ∩ C) \ A = (B \ A) ∩ (C \ A) – дистрибутивний закон віднімання відносно перерізу;
Якщо А є В, то різницю В \ А називають доповненням множини А до множини В і записують - ![]() = В \ А
= В \ А
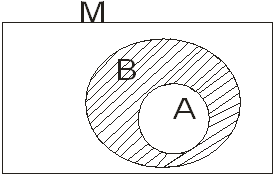
мал.1.10
Отже, доповненням до підмножини А в множину В називається множина всіх елементів із множини В, які не належать А ![]()
Властивості доповнення, якщо ![]() А
А![]() В
В
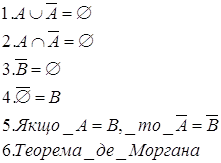
Для довільних підмножин А і В універсальної множини М, доповнення до множин А і В дорівнюють перерізу множин ![]() , а доповнення до перізу множин А і В дорівнює об’єднанню їх доповнень
, а доповнення до перізу множин А і В дорівнює об’єднанню їх доповнень ![]() .
.
Доведемо цей закон за допогою діаграм Ейлера – Венна:
1) ||| = ![]()
![]() ||| =
||| =![]()
![]() ||| =
||| = ![]()
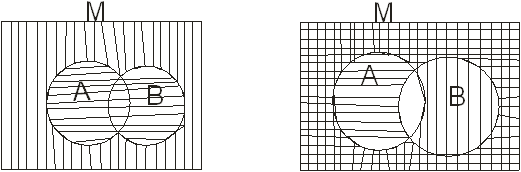
мал.1.11 мал.1.12
2) ![]()
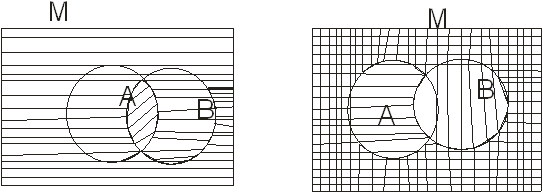
||| = ![]()
![]() ||| -
||| - ![]()
![]()
![]()
# = ![]()
мал.1.3 мал.1.4
Розділ 2. МНОЖИНИ З ВІДНОШЕННЯМ
§ 2. 1. Упорядковані пари. Прямий (декартів) добуток множин.
Множини {1,5} і {5,1}, що містять одні і ті ж самі елементи, рівні, причому запис порядку їх елементів не має значення. Проте, якщо розглядати на площині дві точки А (1,5) і В (5,1), то порядок запису їх координат (1 ; 5) має принципове значення. Можна навести і інші приклади, коли треба врахувати порядок розміщення елементів множини (вектор на площині, вектор у просторі). У зв’язку з цим вводиться поняття упорядкованої сукупності об’єктів, зокрема упорядкованої пари.
Упорядкована пара це двоелементна множина, елементи якої розміщені в певному порядку.
Якщо а є А і b є В, то пару утворену з цих елементів позначають (a; b).
Елемент а називають лівою (першою) координатою (компонентою), а
b – правою (другою) координатою упорядкованої пари (а; b).
Множини А і В тут нерівноправні. При утворенні пари ставимо на перше місце елемент з А, а на друге – елемент з В. Припустимо, що користуючись таким правилом, ми утворили всі можливі пари, в яких на першому місці стоїть елемент з А, а на другому – з В. Множина всіх цих пар і називається прямим добутком.
Прямим (декартовим) добутком множин А і В називається множина усіх можливих пар, перші елементи яких належать множині А, а другій множині В і позначається А х В.
Отже, А х В = {(а; b)| а є А, b є В}
Декартів добуток множин не комутативний
А х В ≠ В х А
А х В = В х А лише тоді, коли А = В або одна із множин порожня.
Щодо асоціативного закону, то йому декарті добуток не підлягає навіть тоді, коли множини А, В і С рівні. Отже, якщо А ≠ Ø, то А х (А х А) ≠ (А х А) х А.
Для прямого добутку справедливі такі дистрибутивні закони:
(А ![]() В) х С = (А х С)
В) х С = (А х С) ![]() (В х С)
(В х С)
А х (В ![]() С) = (А х В)
С) = (А х В) ![]() (А х С)
(А х С)
(А ∩ В) х С = (А х С) ∩ (В х С)
А х (В ∩ С) = (А х В) ∩ (А х С)
А х (В \ С) = (А х В) \ (А х С)
Декартів добуток АхА називають декартовим квадратом і позначається
А ² = А х А = {(a, b) | а є А, b є А}
Декартів добуток множин А, В, С визначається так само як і декартів добуток двох множин
А х В х С = {(a, b, с) | а є А, b є В, с є С}
Декарті добуток А х А х А називається декартовим кубом і позначається
А ³ = А х А х А
Якщо множину дійсних чисел R = (- ∞: + ∞) можна ототожнювати з числовою прямою, то декартів квадрат R х R дійсних чисел можна ототожнювати з числовою площиною. Очевидно, R х R – сукупність всіх можливих упорядкованих пар дійсних чисел (х; y).
Таким чином, числову площину можна розглядати як прямий добуток числової вісі на себе. Якщо представити собі два екземпляри числової вісі, які перетинаються в точці О під прямим кутом, то їх можна розглядати як координатні вісі прямокутної декартової системи на площині.
У зв’язку з цим прямий добуток множин і називають декартовим.
§ 2. 2. Бінарні відношення. Способи задання відношень.
Поняття відношень між множинами відносяться до числа фундаментальних понять математики. І не тільки тому, що воно лежить в основі визначення таких важливих понять математики, як функції і відображення, але й тому, що в будь–якій науці вивчаються не тільки самі об’єкти, але і зв’язки між ними.
Розглянемо бінарне відношення, тобто відношення між двома елементами однієї або різних множин.
Спочатку розглянемо приклад бінарного відношення між елементами двох множин А і В.
А = {Сашко, Борис, Володя, Галя, Таня, Оленка}
В = {футбол, волейбол, плавання, гімнастика, теніс}
За допомогою слів „займатися яким-небудь видом спорту” між елементами цих множин встановлено зв’язок, або, як говорять в математиці, відношення. В результаті ми одержали третю множину Р
Р = {(Сашко, волейбол), (Сашко, теніс), (Борис, футбол),
(Володя, плавання), (Галя, волейбол), (Оленка, теніс)}
Наведений приклад показує, що будь-яке бінарне відношення (відповідність) між елементами множин А і В повністю характеризується трьома множинами: А, В і Р – множиною пар, що є підмножиною А х В.
Р ![]() А х В
А х В![]()
Множину упорядкованих пар Р називають графіком розглядуваного відношення.
Якщо буквою р позначити відношення із А в В, то відповідність р: „учень х є А займається видом спорту у є В залишається: хру.
У математиці досить часто доводиться мати справу з тими чи іншими відношеннями між певними об’єктами.
Найважливіші з них мають певні назви і позначення:
відношення рівності (═); відношення перпендикулярності (![]() ); відношення паралельності (║); відношення подільності
); відношення паралельності (║); відношення подільності ![]() ; відношення включення (
; відношення включення (![]() )
)![]() ; відношення конгруентності (
; відношення конгруентності (![]() ); відношення подібності (~).
); відношення подібності (~).
Бінарне відношення можна задати сукупністю впорядкованих пар, стрілочним і графічним способами.
Стрілочний спосіб полягає в тому, що множини А і В зображають кругами, їх елементи точками. Потім з’єднують стрілками елементи кожної пари (х; у), які належать графіку Р заданого відношення. В результаті одержимо фігуру, яку називають графіком розглядуваного відношення Р
При графічному зображенні відношення Р на площині ставимо точки, які відповідають парам (х; у), що належать відношенню Р. Множина цих точок і буде графіком даного відношення.
§ 2. 3. Властивості бінарних відношень.
Найважливішими властивостями бінарних відношень є рефлексивність, симетричність, транзитивність.
Бінарне відношення р називається рефлексивним, якщо для будь-якої пари (х, х) є А ², елемент х знаходиться у відношенні р сам з собою.
Антирефлексивним називається таке відношення для якого х не знаходиться у відношенні р з х для будь-якої пари (х, х) є А ².
Рефлексивним є, наприклад, такі відношення рівності (═), не більше (≤), подільності (![]() ), рівносильності висловлювань (
), рівносильності висловлювань (![]() ), паралельності (║), конгруентності (
), паралельності (║), конгруентності (![]() ) та подібності (~).
) та подібності (~).
Антирефлексивними є відношення нерівності (≠), більше (>), менше (<), перпендикулярності (![]() ), не подільності (
), не подільності (![]() ).
).
Бінарне відношення р називається симетричним, якщо для пари
(х, у) є А ² із хру випливає урх.
Антисиметричним називається таке відношення для якого для будь-якої пари (х, у) є А ² із хру випливає ![]() .
.
Симетричними є відношення рівності (═), рівносильності (≡), перпендикулярності (![]() ), конгруентності (
), конгруентності (![]() ), подібності (~).
), подібності (~).
Асиметричними є відношення більше (>), менше (<), не більше (≤), включення (![]() ).
).
Бінарне відношення р називається транзитивним, якщо для будь-яких трьох елементів х, у, z з множини А із хру і урz випливає xpz.
Антитранзистивним відношенням називається таке відношення для якого для будь-яких трьох елементів х, у, z з множини А із хру і урz випливає ![]()
Транзитивним є відношення менше (<), не більше (≤), подільності (![]() ), рівносильності (≡), конгруентності (
), рівносильності (≡), конгруентності (![]() ), паралельності (║), подібності (~).
), паралельності (║), подібності (~).
Антитранзистивними є відношення перпендикулярності (![]() ).
).
Відношення між елементами множин можуть мати одну, дві, три або не володіти ні однією властивістю.
Наприклад, відношення перпендикулярності в множині прямих є симетричним, але не має рефлексивної і транзитивної властивостей, відношення р „число х більше числа у” у множині натуральних чисел є транзитивним, але не володіє властивостями рефлективності і симетричності.
§ 2. 4. Відношення еквівалентності.
Бінарне відношення р називається відношенням еквівалентності, якщо воно рефлексивне, симетричне і транзитивне.
Відношення: „бути однокурсником” у множині студентів; „мати один і той же корінь” у множині слів є відношеннями еквівалентності.
Якщо між елементами деякої множини, встановлено відношення еквівалентності, то цим самим ми розбиваємо задану множину на класи.
Розглянемо відношення р: „давати однакову остачу при діленні на 3” у множині невід’ємних цілих чисел. Цим самим ми розбиваємо задану множину на такі класи, які не перетинаються:
К1 = {0, 3, 6, 9 ......} – остача нуль
К2 = {4, 7, 10 ......} – остача один
К3 = {5, 8, 11 ......} – остача два
Класи, на які відношення еквівалентності розбиває множину А називаються класами еквівалентності. Це розбиття характеризується такими властивостями:
1. Ці класи не порожні
Кі ≠ Ø для всіх і = 1, 2, 3, ......, n
2. Будь-які два класи не перетинаються
Кі ∩ Ку = ![]() для будь-яких і, у = 1, 2, 3, ......, n
для будь-яких і, у = 1, 2, 3, ......, n
3. Об’єднання усіх класів дає універсальну множину А
![]() Кі = А
Кі = А
Легко переконатися, що елементи із одного класу еквівалентні між собою, а елементи із різних класів – ні.
Теорема
Будь-яке відношення еквівалентності р здійснює розбиття множини А на класи еквівалентності так, що будь-які два елементи одного класу знаходяться у відношенні р, а будь-які два елементи різних класів не знаходяться у даному відношенні між собою.
Доведення
Нехай в множині А є відношення еквівалентності р. Візьмемо з цієї множини якийсь елемент а і виділимо в окремий клас К (а) всі елементи, які знаходяться з а у відношенні р
К (а) = {у | у є А, ару} (1)
Задане відношення р розіб’є всю множину А на ряд класів К, в результаті чого ми одержимо множину класів {К (а)}.
Доведемо, що множина {К (а)} для всіх а є А є розбиттям на класи, тобто що вона задовольняє трьом умовам розбиття на класи, а саме, що:
1) К (а) ≠ Ø
2) К (а) ∩ К (b) = Ø
3) ![]() К (а) = А
К (а) = А
Покажемо, що справедлива перша умова.
Раз р є відношенням еквівалентності, то воно є рефлексивне, тобто ара. Значить К (а) має хоча б один елемент а і вже К (а) не порожня множина
К (а) ≠ Ø
Покажемо, що справджується умова 2) для будь-яких а і b є А,
якщо а ![]() b.
b.
Доведемо цю умову виходячи з протилежного.
Припустимо, що К (а) ∩ К (b) ≠ Ø. Тоді у них є спільний елемент с, тобто
с є К (а) і с є К (b)
Але елементи одного класу, відповідно до (1) знаходяться у відношенні р між собою, значить
арс і bрс
Із симетричності відношення р із bрс слідує срb, а із транзитивності відношення р випливає:
якщо арс і срb, то арb.
А це протирічить умові, що а![]() b.
b.
Значить, припущення не вірне і
К (а) ∩ К (b) = Ø.
Покажемо, що виконується і умова 3).
Із формули (1) видно, що будь-який а є А належить класові К (а), тобто
а є К (а). Отже, щоб одержати множину А треба об’єднати усі ці класи
![]() К (а) = А
К (а) = А
а є А
Ми довели, що відношення р розбиває множину А на класи еквівалентності.
Тепер покажемо, що: 1) два елементи одного класу еквівалентні між собою, а 2) два елементи різних класів не еквівалентні. Доведемо перше.
Нехай b і с будь-які два елементи одного класу К (а). Доведемо, що bрс. Раз b є К (а), то по формулі (1) – арb, а з того, що с є К (а) слідує, що арс. За симетричністю відношення р – з а р b слідує b р а. За транзитивністю відношення р маємо bра і арс, то bрс.
Доведемо друге. Нехай маємо два різні класи К (b) ≠ К (с). Покажемо, що b ![]() с. Доведемо від супротивного. Припустимо, що bрс. Нехай d – довільний елемент множини К (с), тоді cpd.
с. Доведемо від супротивного. Припустимо, що bрс. Нехай d – довільний елемент множини К (с), тоді cpd.
За симетричністю р маємо із bрс слідує срb.
За транзитивністю із bрс і срd слідує bpd.
Значить d є К (b).
Ми довели, що якщо d є К (с), то d є К (b) для вільного d.
Отже, К (с) ![]() К (b).
К (b).
Аналогічно доводимо, що К (b) ![]() К (с).
К (с).
Отже, К (b) = К (с). ![]()
А це протирічить умові. Значить, наше припущення не вірне і ![]() b
b![]() с.
с.
§ 2. 5. Відношення порядку. Упорядкована множина.
Серед різних відношень ми часто зустрічаємо такі, які встановлюють у множині певний порядок.![]()
Інтуїтивне представлення про порядок об’єктів переважно пов’язано з їх взаємним розміщенням в просторі (вище – нижче, ближче – дальше, правіше – лівіше); в часі (раніше – пізніше); з порівнянням їх розмірів (більше – менше, легше – тяжче).
Ці відношення і подібні їм відносяться до важливого класу відношень, що називають відношеннями порядку.
Відношенням строгого порядку називається будь-яке відношення, яке є антирефлексивним, антисиметричним і транзитивним.
Отже, відношення р буде відношенням строгого порядку, якщо:
1. х![]() х для будь-якого х є А, тобто (х, х)
х для будь-якого х є А, тобто (х, х) ![]() Р для будь-якої пари
Р для будь-якої пари
2. (х, х) є А ².
3. якщо хру , то у![]() х для будь - якого
х, у є А, тобто якщо (х, у) є Р, то
х для будь - якого
х, у є А, тобто якщо (х, у) є Р, то
(у, х) ![]() Р для будь-якої пари (х, у) є А ².
Р для будь-якої пари (х, у) є А ².
Похожие работы
... . Поклавши у формулі (4) а = b = 1, дістанемо Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ § 1. Про предмет теорії ймовірностей До цього часу розглядалися задачі, в яких результат дії був однозначно ...
... структуро творча одиниця діяльності (операція діяльності) КОМБІНАТОРИКА ФОРМОТВОРЕННЯ Комбінаторика — математичний термін, запозичений теорією і практикою художнього проектування. Комбінаторика в дизайні — особливий творчий підхід до формотворення, заснований на пошуку і дослідженні закономірностей варіантної зміни просторових структур, а також способів упорядкування проектування об'єктів ...
... . 5. Існують 4 точки неколлінеарні по трьох. Тоді кінцева множина P точок і множина L прямих утворить кінцеву проективну площину. Для знаходження кусково-постійних конфігурацій множин треба спочатку на множині усіх множин ввести Р(D) лінійні бінарні відношення та =. Матимемо частково впорядковану множину . Потім знаходимо ті групи множин, які у заданій конфігурації розташовані поряд і які ...
... речовин мармелад випускають різних найменувань: яблучний, сливовий, абрикосовий, полуничний та інші. З.Г. Скобельська, Г.Н. Горячева «Технологія виробництва цукрових кондитерських виробів» в залежності від застосованого драглеутворюючого компонента мармеладні вироби поділяють на чотири групи: з натуральними чистими драглеутворювачами – агар-агаром, агароїдом, фурцелараном, пектином (желейні ...


0 комментариев