Навигация
1. х – парне число
2. Поет х написав поему “ Сон”.
Ці речення не є висловленням, бо неможна сказати чи вони “і” чи “х“. Якщо змінну в першому реченні замінити числом, а в другому прізвищем поета, то вони перетвореться у висловлення.
Предикатом називається твердження, в яке входять вільні змінні і яке при заміні їх коректними значеннями стає висловленням.
Це є одномісні предикати.
Для кожного предиката треба, вказати множину значень, які може приймати змінна х. Цю множину називають областю визначення предиката і в першому прикладі область визначення – N, у другому - множина прізвищ поетів.
Предикат позначають великими буквами:
P(x), Q(x), R(x), S(x), де х 
Х.
Множина тих
значень змінних, при яких предикат набуває істиного значення називається областю істинності предиката і позначається Т. Область істиності є підмножиною області визначення Т 
Х.
У першому прикладі Т = {x | x N i є парне}
У другому прикладі Т = { Шевченко }
Предикат в який входить дві змінні називаються двомісним. Приклади:
1. x > y;
2. “Поет х написа поему у “
Двомісні предикати позначаються P(x, y), Q(x, y) які визначені на множенні Х × У.
В математиці зустрічаються багато предикатів, причому деякі з них мають спеціальні позначення
„х = у“; „х < у“; „х ║ у“; „х 
у“ і т.д.
В математиці зустрічається і трьох, чотирьох і т.д. місні предикати. Приклади:
1. Число х ділиться на число у і на число z.
2. Всі числа, які діляться на х і у, діляться і на z.
3. Сума чисел х і у дорівнює добутку чисел U і V.
4. а1х1 + а2х2 + а3х3 + … + аnxn = b n–місний предикат
Нехай Q (a, b) – двомісний предикат.
(a - b)² = а² – 2ab + b². Цей предикат перетворюється на істинне висловлення при всіх дійсних значеннях „a” і „b”. Областю істинності предиката Q є множина всіх дійсних чисел R. Такий предикат називається тотожно істинним.
Рівності, рівняння, нерівності та їх системи, що розглядаються в математиці, з точки зору логіки – предикати.
§ 3. 4. Квантори.
У математиці часто використовують вирази „для всіх”, „для кожного”, „яке б не було”, „існує”, „знайдеться хоча б одне”.
Для позначення цих виразів вживаються символи, які називаються кванторами: квантор загальності , який позначається 
, у звичайній мові йому відповідає вираз „для кожного”, „для всякого”, „для всіх”.
Нехай Р(х) – „Трикутник х прямокутний», то вираз (х є Х) Р(х) читається:
1. Будь-який трикутник прямокутний
2. Кожний трикутник прямокутний
3. Всі трикутники прямокутні
Усі ці висловлення є хибними. Отже, в результаті квантифікації (приписуванні кватора) предикат перетворюється у висловлення. Цей квантор називається квантором загальності.
Розглянемо ще квантор існування, який позначається 
. У звичайній мові йому відповідає вираз: „існує”, „знайдеться хоча б одне”.
Нехай Р(х): „х > 5”
Вираз ( х є R) (х > 5) читається:
1. Існує дійсне число х таке, що х > 5
2. знайдеться таке дійсне число х, яке > 5
3. хоча б одне дійсне число > 5
В результаті квантифікація, навішування квантора на змінну предикат перетворився у висловлення.
Над предметами, так само, як і над множинами можна проводити операції кон’юнкцію, диз’юнкцію, заперечення, імплікацію і еквіваленцію.
§ 3. 5. Поняття про теореми.
Які б ми розділи математики не розглядали скрізь ми зустрічаємось з твердженнями, які називаємо теоремою.
Теорема – це математичне твердження, істинність якого з’ясовується доведенням (міркуванням).
Формулювання будь-якої теореми складається з двох частин: умови і висновку, який випливає з даної умови.
Розглянемо приклад. Теорема: „Якщо точка лежить на бісектрисі кута, то вона рівновіддалена від сторін цього кута”.
Якщо умову позначити через Р (х), то вона буде виражатися реченням: „Точка лежить на бісектрисі”, а висновок позначити через Q (х), то це буде речення „Точка рівновіддалена від сторін кута”. Як умова так і висновок є предикатами, які задані на множині Х всіх точок площини. Тому дану теорему можна записати у вигляді
(х є Х) (Р(х) 
Q (х))
Отже, в цій теоремі ми виділили такі три частини:
1. Умова теореми: предикат Р (х), заданий на множині Х усіх точок площини.
2. Висновок теореми: предикат Q (х), який заданий на множені Х
3. Пояснювальна частина х є Х: в ній описується множина об’єктів, про які йде мова в теоремі.
Умова і висновок не завжди є елементарними висловленнями, а можуть мати складну логічну структуру, найчастіше кон’юктивну або диз’юнктивну.
Наприклад:
Похожие работы
... . Поклавши у формулі (4) а = b = 1, дістанемо Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ § 1. Про предмет теорії ймовірностей До цього часу розглядалися задачі, в яких результат дії був однозначно ...
... структуро творча одиниця діяльності (операція діяльності) КОМБІНАТОРИКА ФОРМОТВОРЕННЯ Комбінаторика — математичний термін, запозичений теорією і практикою художнього проектування. Комбінаторика в дизайні — особливий творчий підхід до формотворення, заснований на пошуку і дослідженні закономірностей варіантної зміни просторових структур, а також способів упорядкування проектування об'єктів ...
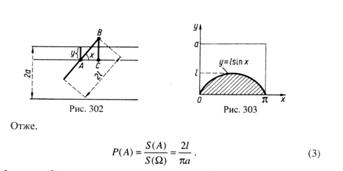
... . 5. Існують 4 точки неколлінеарні по трьох. Тоді кінцева множина P точок і множина L прямих утворить кінцеву проективну площину. Для знаходження кусково-постійних конфігурацій множин треба спочатку на множині усіх множин ввести Р(D) лінійні бінарні відношення та =. Матимемо частково впорядковану множину . Потім знаходимо ті групи множин, які у заданій конфігурації розташовані поряд і які ...
... речовин мармелад випускають різних найменувань: яблучний, сливовий, абрикосовий, полуничний та інші. З.Г. Скобельська, Г.Н. Горячева «Технологія виробництва цукрових кондитерських виробів» в залежності від застосованого драглеутворюючого компонента мармеладні вироби поділяють на чотири групи: з натуральними чистими драглеутворювачами – агар-агаром, агароїдом, фурцелараном, пектином (желейні ...
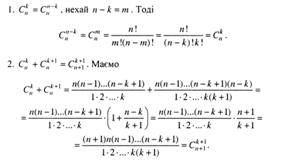
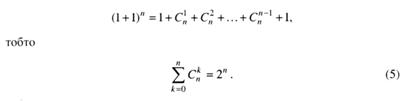
0 комментариев