Навигация
Якщо хру і урz, то хрz для будь-яких х, у, z є А, тобто якщо (х, у) є Р і (у, z) є Р, то і (х, z) є Р для будь яких пар (х, у) (у, z) є А ²
4. якщо хру і урz, то хрz для будь-яких х, у, z є А, тобто якщо (х, у) є Р і (у, z) є Р, то і (х, z) є Р для будь яких пар (х, у) (у, z) є А ².
Так відношення р: „ х < у у множині А = {1, 2, 3, 4, 5} є відношенням строгого порядку, тому що воно антирефлексивне, антисиметричне, транзитивне.
Відношення р називається відношенням нестрогого (часткового) порядку, якщо воно рефлексивне, антисиметричне і транзитивне.
Так, відношення „число х – дільник числа у” у множині А = {1, 2, 3, 4, 5} є відношенням часткового порядку, тому що воно транзитивне, рефлексивне і антисиметричне.
У математиці та її застосуваннях особливу роль відіграють такі відношення порядку р, які дають можливість порівняти довільні різні елементи певної множини А. Ці відношення називаються відношеннями лінійного порядку у множині А.
Відношення строгого (нестрогого) порядку називається відношенням лінійного строгого (нестрогого) порядку, якщо для будь-яких різних елементів х і у із А здійснюється одне із відношень хру або урх.
Проілюструємо сказане на прикладі. Нехай А – множина студентів групи. Р – відношення „студент х вищий за студента у”. Це відношення антирефлексивне, антисиметричне і транзитивне.
Значить, воно відношення строгого порядку. Якщо в даній множині А немає студентів однакового росту, то тоді про будь-яких двох студентів можна сказати, що або студент х вищий за у або студент у вищий студента х. Отже, відношення Р є відношенням строгого лінійного порядку.
Множина А називається лінійною упорядкованою, якщо в А введено відношення Р і для будь-якої пари (х, у) є А ², якщо х ≠ у, то хру або
урх.
Так, множина натуральних чисел лінійно упорядкована відношенням строгого порядку „менше”, тобто N = {1, 2, 3, 4, ....}
Розділ 3. СИМВОЛІКА МАТЕМАТИЧНОЇ ЛОГІКИ
§ 3. 1. Поняття висловлення
Під математичною логікою або символічною логікою розуміють логіку, що розвивається за допомогою математичних методів. Математичний апарат до логіки вперше застосував у XIX ст. англійський математик Джордж Буль.
Д. Буль (1815 – 1864 р.р.), батько відомої англійської письменниці Войнич (її чоловік був революціонером), автора роману „Овод”. Темп розвитку математичної логіки різко зростає у XIX ст. У 90-х роках ХХ ст.. математична логіка дістає широке застосування в технічних науках, наприклад, електротехніці. Зараз вона є складовою частиною теоретичного фундаменту кібернетики.
Основним поняттям математичної логіки є висловлювання. Висловлювання належить до первинних понять, воно не визначеється через інші поняття, а вводяться за допомогою опису.
Під висловлюванням розуміють будь-яке твердження, відносно якого можна з’ясувати, істинне воно чи хибне. Наприклад,![]()
1. Діагональ квадрата не сумірна з його стороною – „і” висловлювання
2. 5 > 8 – „х” висловлення
3. О котрій годині ти повернешся вчора додому? – не є висловленням.
Висловлення позначаються малими латинськими буквами: p, q, r, s, ......
Множину усіх висловлювань, яку позначимо буквою S, ділять на дві підмножини (класи)
Т – клас усіх істинних висловлювань
F – клас усіх хибних висловлювань
Два висловлювання p і q називаються рівносильними (логічно рівними), якщо вони належать до одного й того самого класу і записують
p ![]() q
q
Із означення рівносильності висловлювань виникають властивості:
1. р ![]() р
р
2. Якщо р ![]() q, то q
q, то q ![]() р – симетричність
р – симетричність
3. Якщо р ![]() q і q
q і q ![]() r,то р
r,то р ![]() r – транзитивність
r – транзитивність
§ 3. 2. Операції над висловленнями
У розмовній мові для сполучення двох речень вживають слова: і, або, якщо ...... то, тоді і тільки тоді, не. З’ясуємо те значення, в якому ці слова вживаються в логіці.
а) Логічне множення (кон’юнкція)
Логічним добутком (кон’юнкцією) двох висловлень p і q називається
таке висловлення „p і q”, яке істинне тоді і тільки тоді, коли p і q одночасно істинні. Позначається: p ![]() q.
q.
Згідно з означенням маємо таку таблицю істинності для кон’юнкції.
| p | q | p |
| i | i | i |
| i | x | x |
| x | i | x |
| x | x | x |
Приклад. Нехай висловлення р буде “5<8”, а висловлення q – “ 8 < 13 “, тоді кон’юнція цих висловлень буде “ I ”, бо істинне p i q .
Переважно скорочено таку кон’юнкцію записують як подвійну нерівність 8 < 5 < 13
Властивості кон’юнкції
1) Комутативна (переставна властивість) p ![]() q
q ![]() q
q ![]() p
p
| p | q | p | q |
| і | і | і | і |
| і | х | х | х |
| х | і | х | х |
| х | х |
|
|
![]()
2) Асоціативна (сполучна) властивість (p ![]() q)
q) ![]() s
s ![]() p
p ![]() (q
(q ![]() s)
s)
| p | q | s | (p | (p | (q | (q |
| і | і | і | і | і | і | і |
| і | х | х | х | х | х | х |
| х | і | х | х | х | х | х |
| х | х | і | х | х | х | х |
| х | і | і | х | х | і | х |
| і | х | і | х | х | х | х |
| і | і | х | і | х | х | х |
| х | х | х | х | х | х | х |
![]()
![]()
![]()
![]()
Означення кон’юнкції двох висловлювань розповсюдна на будь-яке скінченне число висловлювань
![]() рі = р1
рі = р1![]() р2
р2![]() р3
р3![]() р4
р4![]() …
…![]() рn
рn
б) Логічне додавання (диз’юнкція)
Диз’юнкцією або логічною сумою двох висловлень p і q називається висловлення “p і q „ яке істинне тоді і тільки тоді, коли істинне хоча б одне із висловлювань і хибне коли вони обидва хибні.
Позначення диз’юнкції: p v q
Таблиця істинності:
| p | q | p v q |
| i | i | i |
| i | x | і |
| x | i | і |
| x | x | x |
Закони диз’юнкції
1) Комутативний: p v q ![]() q v p
q v p
| p | q | p v q | q v p |
| і | і | і | і |
| і | х | і | і |
| х | і | і | і |
| х | х |
|
|
![]()
2) Асоціативний закон диз’юнкції (p v q) v s ![]() p v (q v s)
p v (q v s)
| p | q | s | p v q | (p v q) v s | q v s | p v (q v s) |
| і | і | і | і | і | і | і |
| і | х | х | і | і | х | і |
| х | і | х | і | і | і | і |
| х | х | і | х | і | і | і |
| х | і | і | і | і | і | і |
| і | х | і | і | і | і | і |
| і | і | і | і | і | і | і |
| х | х | х | х |
| х |
|
![]()
![]()
3) Дистрибутивні закони, які пов’язують кон’юнкцію і диз’юнкцію
(p v q) ![]() s
s ![]() (p
(p ![]() s) v (q
s) v (q ![]() s)
s)
(p ![]() q) v s
q) v s ![]() (p v s)
(p v s) ![]() (q v s)
(q v s)
Довести дома самостійно.
в) Заперечення висловлення
Запереченням висловлення р називається висловлення „не р“, яке істинне, коли р хибне, і хибне коли р істинне.
Позначення : ![]() .
.
| р |
|
| і | х |
| х | і |
Закони заперечення
1) Заперечення заперечення висловлення рівносильне висловленню р:
![]()
![]() р
р
2) Закон суперпозиції
p ![]()
![]()
![]() х
х
| р |
| p |
| і | х | х |
| х | і | х |
3) Закон включення третього
q v ![]()
![]() i
i
Кожне висловлення q або істинне або хибне, третього не може бути q v ![]() = i
= i
| q |
| q v |
| і | х | i |
| х | і | i |
4) Закони де Моргана
![]()
![]()
![]() v
v ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Заперечення кон’юнкції двох висловлень рівносильне диз’юнкції заперечень і заперечення диз’юнкції рівносильне кон’юнкції заперечень цих висловлень.
![]()
![]()
![]() v
v ![]()
| р | q | p |
|
|
|
|
| і | i | i | х | x | x | x |
| i | x | x | і | x | i | i |
| x | i | x | i | i | x | i |
| x | x | x |
| x | x |
|
г) Логічне слідування (імплікація)
Слідуванням (імплікацією) двох висловлень p і q називається висловлення “якщо p, то q„, яке хибне тоді і тільки тоді, коли p – істинне, а q – хибне. Позначається імплікація: p ![]() q
q
| p | q | p |
| i | i | i |
| i | x | x |
| x | i | і |
| x | x | i |
Операцію імплікації двох висловлень можна виразити через операцію заперечення і диз’юнкцію:
p ![]() q
q ![]()
![]() v q
v q
| p | q | p |
|
|
| i | i | i | x | і |
| i | x | x | x | х |
| x | i | і | i | і |
| x | x | i | i | і |
![]()
![]()
![]()
д) Еквіваленція (рівносильність) двох висловлень
Еквіваленцією (рівносильністю) двох висловлень p і q називається висловлення „р тоді, і тільки тоді, коли q, яке істинне тоді і тільки тоді, коли p і q одночасно істинні, або одночасно хибні“
Позначається: p ![]() q , p
q , p ![]() q
q
Еквіваленція
(p ![]() q)
q) ![]() (p
(p ![]() q
q ![]() q
q ![]() p)
p)
| p | q | p | p | q | p |
| i | i | і | i | і | і |
| i | x | х | x | і | х |
| x | i | х | і | х | х |
| x | x | і | i | i | і |
![]()
![]()
![]()
§ 3.3. Предикати
(неозначуване висловлення або висловлювальна форма)
Розглянемо речення
Похожие работы
... . Поклавши у формулі (4) а = b = 1, дістанемо Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ § 1. Про предмет теорії ймовірностей До цього часу розглядалися задачі, в яких результат дії був однозначно ...
... структуро творча одиниця діяльності (операція діяльності) КОМБІНАТОРИКА ФОРМОТВОРЕННЯ Комбінаторика — математичний термін, запозичений теорією і практикою художнього проектування. Комбінаторика в дизайні — особливий творчий підхід до формотворення, заснований на пошуку і дослідженні закономірностей варіантної зміни просторових структур, а також способів упорядкування проектування об'єктів ...
... . 5. Існують 4 точки неколлінеарні по трьох. Тоді кінцева множина P точок і множина L прямих утворить кінцеву проективну площину. Для знаходження кусково-постійних конфігурацій множин треба спочатку на множині усіх множин ввести Р(D) лінійні бінарні відношення та =. Матимемо частково впорядковану множину . Потім знаходимо ті групи множин, які у заданій конфігурації розташовані поряд і які ...
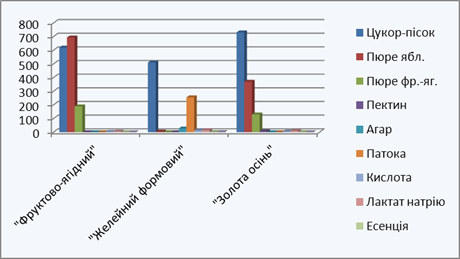
... речовин мармелад випускають різних найменувань: яблучний, сливовий, абрикосовий, полуничний та інші. З.Г. Скобельська, Г.Н. Горячева «Технологія виробництва цукрових кондитерських виробів» в залежності від застосованого драглеутворюючого компонента мармеладні вироби поділяють на чотири групи: з натуральними чистими драглеутворювачами – агар-агаром, агароїдом, фурцелараном, пектином (желейні ...
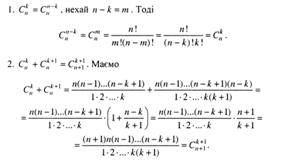
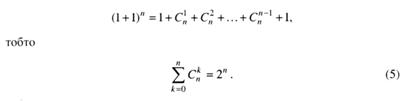


0 комментариев