Навигация
Дослідження моделей міжгалузевих балансів
4.4 Дослідження моделей міжгалузевих балансів
Модель міжгалузевих балансів на відміну від моделі "витрати-випуск" Леонтьєва містить ще деякі дані. В табл. 4.2. наведена загальна схема міжгалузевого балансу виробництва та розподілення продукції.
Ця схема включає чотири квадранти. Перший квадрант – це шахматна таблиця міжгалузевих потоків продукції. В другім квадранті показана кінцева продукція усіх галузей. Третій квадрант характеризує умовно-чисту продукцію, до якої відносяться амортизаційні відрахування, оплата праці, чистий доход, тощо. Складові третього квадранту можна знайти за формулою
Ei=Xi-![]() ,
, ![]() .
.
Четвертий квадрант знаходиться на перетині стовпця другого квадранту та рядку третього квадранту. Він складається із одного показника і служить для контролю правильності розрахунків: сума елементів другого квадранту має дорівнювати сумі елементів третього квадранту.
Користуючись даними попереднього підрозділу розробити схему міжгалузевого балансу виробництва та розподілення продукції.
Виділяють модифікації моделі міжгалузевого балансу. Для побудови міжгалузевого балансу витрат праці (табл. 4.3) необхідно задати кількість трудових ресурсів
Таблиця 4.2
Міжгалузевий баланс виробництва та розподілення продукції
| Виробляючі галузі | Споживаючі галузі | Кількість Кінцевої продукції | Кількість валової продукції | |
| 1 | 2 | |||
| 1 2 | X11 X21
| X12 X22 I | Y1 Y2 II
| X1 X2
|
| Кількість умовно-чистої продукції | E1 | E2 III | IV | |
| Кількість валової продукції | X1 | X2 | ||
Tаблиця 4.3
Міжгалузевий баланс витрат праці
| Виробля ючі галузі | Споживаючі галузі | |||
| Міжгалузеві витрати упредметненої праці | Витрати праці на кінцеву про дукцію | Витрати праці в галузях (трудові ресурси) | ||
| 1 | 2 | |||
| 1 | M11 | M12 | M1 |
|
| 2 | M21 | M22 | M2 |
|
Для пошуку коефіцієнтів прямої трудомісткості можна використати формулу
![]()
де ![]() - кількість трудових ресурсів, необхідних для виробництва продукції j-ї галузі,
- кількість трудових ресурсів, необхідних для виробництва продукції j-ї галузі, ![]() - обсяг валової продукції j-ї галузі.
- обсяг валової продукції j-ї галузі.
Вектор-рядок коефіцієнтів повної трудомісткості знаходимо за формулою
![]()
де G – матриця повних матеріальних витрат, ![]() - вектор-рядок коефіцієнтів прямої трудомісткості
- вектор-рядок коефіцієнтів прямої трудомісткості ![]() .
.
Помножуючи всі рядки першого та другого квадрантів міжгалузевого балансів на відповідні коефіцієнти прямої трудомісткості, одержуємо схему міжгалузевого балансу витрат праці. Тепер повинно виконуватись рівняння
![]() .
.
На основі міжгалузевого балансу виробництва та розподілення продукції (табл.4.2) побудувати міжгалузевий баланс витрат праці (табл.4.3). Використати таку кількість трудових ресурсів: 120i люд.-днів та 200i люд.-днів, де і – номер заданого варіанту.
Похожие работы
... нашої транспортної задачі: Відповідь: розроблений план перевезень дає можливість отримати мінімальні витрати у розмірі 237,5 грошових одиниць Завдання 4 Побудувати лінійну модель регресивного аналізу для економічного показника, зміни якого спостерігалися в певному інтервалі часу. Контрольний термін 1 2 3 4 5 6 7 8 9 10 Значення показника 9 16 20 27 34 39 44 ...
... : Приведемо її до канонічної форми і доповнимо її базисами: Повернемось до заміни: x1=0 x2=6 Завдання 4. Транспортна задача Для заданих транспортних задач скласти математичну модель і розв’язати їх методом потенціалів, використавши для визначення початкового плану метод мінімального елемента або північно-західного кута. 1. ...
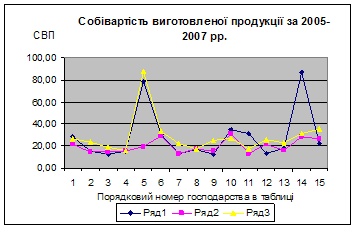
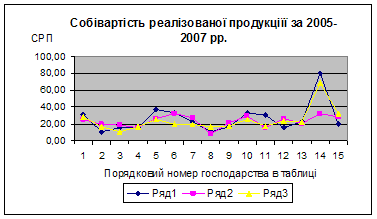
... змін, спостерігається тільки нестабільність та по деяких господарствах різкі зміни собівартості продукції, що виготовляється та реалізується. 3. Економіко-математичне моделювання в управлінні підприємством 3.1 Економіко-математичне моделювання урожайності сільськогосподарської продукції методом Брандона. Нехай економіко-математична модель матиме вид: , Де =; =; = ; Y - ...
... модель, яка опосередковує відносини між об’єктом, який вивчається, та суб’єктом, який пізнає (системним аналітиком). Головним гальмом для практичного застосування математичного моделювання в економіці є проблема наповнення розроблених моделей конкретною та якісною інформацією. Точність і повнота первинної інформації, реальні можливості її збору й опрацювання справляють визначальний вплив на виб ...

0 комментариев