Навигация
Дослідження моделі Неймана
28744
знака
8
таблиц
3
изображения
4.5 Дослідження моделі Неймана
Модель Неймана на відміну від моделі Леонтьєва, в якій розглядається тільки один виробничий цикл, носить динамічний характер.
В моделі Неймана розглядається економіка, яка описується базисними виробничими процесами (галузями або підприємствами).
Кожен базисний процес можна зобразити в вигляді
(
), 
,
де 
- вектор витрат, 
- вектор випуску. Зміст процесу 
такий: він витрачає вектор =(a'ij), 
, та випускає вектор =(x'ij), , тобто переробляє вектор в вектор . Ці вектори невід'ємні. Позначимо через A' та X' матриці
A'=(
),
X'=(
).
Модель задається парою невід'ємних матриць A' та X'. Матриця A' називається матрицею витрат, матриця X' - матрицею випуску.
Комбінуючи базисні процеси, можна одержати нові виробничі процеси. Якщо взяти невід'ємний вектор-стовпець 
, , то можна описати новий виробничий процес
в якому витрати характеризує вектор 
, а випуск – вектор 
.
Нові процеси показують режим спільної роботи різних галузей. Отриманий виробничий процес позначимо (A'
,X') .
Вектор-стовпець називається вектором інтенсивностей.
Модель Неймана лінійна та замкнута. Замкнутість моделі можна показати таким чином.
Нехай для виробництва в (t+1)-й період можна витрачати тільки ті товари, які були вироблені в попередній t-й період. Через 
позначимо вектор запасів, які є до початку всього планового періоду [1,Т]. Запишемо нерівності
A' (1) ≤ ,
A' (2) ≤ X'(1),
A' (t+1) ≤ X'(t),
t=1,...,(T-1).
Позначимо також через 
вектор цін
= (pi), ,
де pi - ціна одиниці і-го товару.
За матрицями A' та X' технологічних процесів, вектором цін та вектором знайти інтенсивності технологічних процесів, які максимізують вартість випуску продукції за один виробничий цикл, та саму цю максимальну вартість.
Для пошуку вектору інтенсивностей =
та максимальної вартості необхідно використати задачу лінійного програмування. Цільову функцію можна зобразити в вигляді.
X'→max.
Обмеження будуть такі
A'≤ ,
≥0.
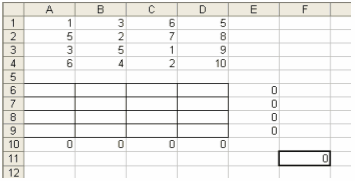
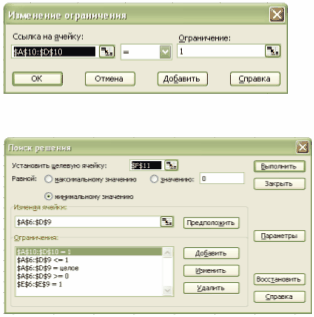
Зобразимо цю задачу у розгорнутій формі
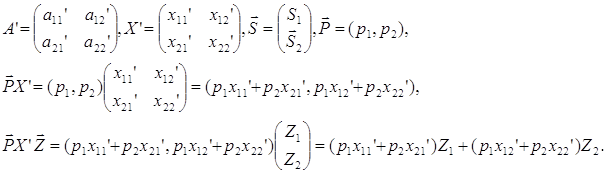
Обмеження в розгорнутій формі мають такий вигляд
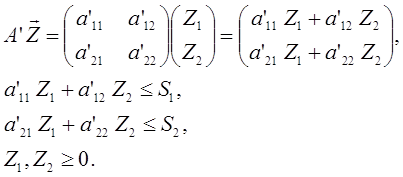
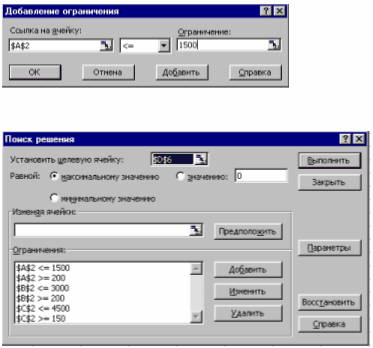
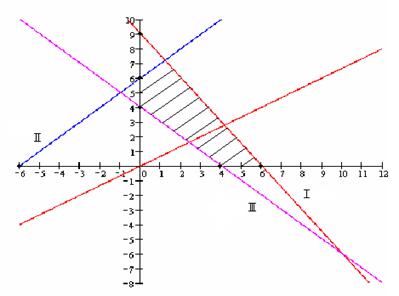
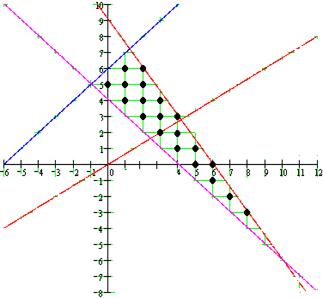
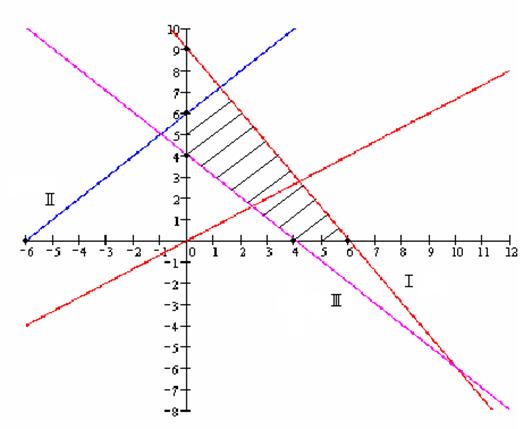
Для розв'язання задачі використати графічний метод. Побудувати координатну площину Z1, Z2 . Використовуючи обмеження, побудувати випуклий многокутник. Далі знайти перетин цільової функції з тією вершиною, де значення цільової функції найбільше. Координати вершини дають необхідні інтенсивності. Знайдені інтенсивності підставляють у цільову функцію для визначення максимальної вартості.
Похожие работы
... нашої транспортної задачі: Відповідь: розроблений план перевезень дає можливість отримати мінімальні витрати у розмірі 237,5 грошових одиниць Завдання 4 Побудувати лінійну модель регресивного аналізу для економічного показника, зміни якого спостерігалися в певному інтервалі часу. Контрольний термін 1 2 3 4 5 6 7 8 9 10 Значення показника 9 16 20 27 34 39 44 ...
... : Приведемо її до канонічної форми і доповнимо її базисами: Повернемось до заміни: x1=0 x2=6 Завдання 4. Транспортна задача Для заданих транспортних задач скласти математичну модель і розв’язати їх методом потенціалів, використавши для визначення початкового плану метод мінімального елемента або північно-західного кута. 1. ...
... змін, спостерігається тільки нестабільність та по деяких господарствах різкі зміни собівартості продукції, що виготовляється та реалізується. 3. Економіко-математичне моделювання в управлінні підприємством 3.1 Економіко-математичне моделювання урожайності сільськогосподарської продукції методом Брандона. Нехай економіко-математична модель матиме вид: , Де =; =; = ; Y - ...
... модель, яка опосередковує відносини між об’єктом, який вивчається, та суб’єктом, який пізнає (системним аналітиком). Головним гальмом для практичного застосування математичного моделювання в економіці є проблема наповнення розроблених моделей конкретною та якісною інформацією. Точність і повнота первинної інформації, реальні можливості її збору й опрацювання справляють визначальний вплив на виб ...
0 комментариев