Навигация
4.6 Дослідження моделі Солоу
Стан економіки в моделі Солоу задається змінними:
Y- кінцева продукція;
L- трудові ресурси;
K- основні виробничі фонди або виробничий капітал;
І – інвестиції;
С – продукція невиробничого споживання.
Всі змінні взаємопов'язані (рис.4.1)
Назвемо нормою накопичення ρ долю кінцевої продукції, яка використовується в інвестиціях. Тоді
I=ρY,
C=(1-ρ)Y,
0<ρ<1.
Інвестиції використовуються для відновлення фондів, які вибувають, та на їх приріст. Приймемо, що фонди вибувають із постійним коефіцієнтом вибування μ, 0<μ<1..
Також зробимо припущення, що інвестиції у тому ж році повністю витрачаються на приріст ОВФ та на амортизацію. В дискретному варіанті цей зв'язок має вигляд
IΔt=ΔK+DΔt,
де Δt - приріст часу, ΔK - приріст капіталу, D - амортизаційні відрахування.
Перепишемо останній вираз у формі
ΔK=IΔt-DΔt,
ΔK=Δt(I-D),
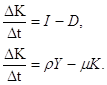
Тут амортизаційні відрахування дорівнюють D=μK.
У випадку неперервного часу аналогом останнього рівняння є
.
Якщо вважати, що приріст трудових ресурсів пропорційний наявним трудовим ресурсам (ΔL=nLΔt) , то одержуємо диференційне рівняння
де n - доля приросту трудових ресурсів.
Розв'язання рівняння дає
L=L0ent,
де L0 = L(0) - трудові ресурси на початку спостереження (для t=0).
Модель Солоу задається системою рівнянь
C=(1-ρ)Y,
Y=f(K,L),
L=L0ent,
,
K(0)=K0.
На початку спостереження основні фонди дорівнюють K0.
Розглянемо стаціонарну траєкторію, на якій середня фондоозброєність
k = 
,
постійна і дорівнює своєму початковому значенню:
k(t) = const = k0.
Позначимо стаціонарне значення фондоозброєності через 
. Для функції Кобба-Дугласа
Y1= f(K1,L1)=F(K1,L1)/2=aK1αL11-α /2,
воно обчислюється за формулою
1= [ρa /( 2μ +2 n)]1/(1 - α).
Середня продуктивність праці y=
.
На стаціонарній траєкторії позначимо продуктивність праці 
. Для функції Кобба-Дугласа можна знайти за формулою:
1=a[ρa / (2μ +2 n)]α / (1 - α) / 2.
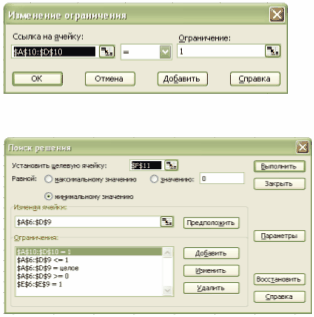
За даними для функції Кобба-Дугласа (п.4.2) та нормою накопичення ρ=0.02і, коефіцієнтом вибування фондів μ=0,03і за рік, долею приросту трудових ресурсів n=0,05і знайти значення фондоозброєності та продуктивності праці на стаціонарній траєкторії. Тут і – номер заданого варіанту.
Дослідити модель Солоу для лінійної виробничої функції (п.4.2)
Y2=(b1K2+b2L2)/2,
b1=10i, b2=і,
де і – номер заданого варіанту.
На основі використання рівняння
визначити математичні вирази для 
та 
. Обчислити їх значення, підставляючи у вирази чисельні значення 
. Проставити одиниці вимірювання.
4.7 Побудова схеми алгоритму
У цьому підрозділі необхідно побудувати схему алгоритму програми. Як відомо, алгоритм – це точно визначена послідовність операцій над об'єктами. В схемі необхідно використати блоки початку та кінця, блоки вводу та виводу даних, обчислювальні та логічні блоки. Потрібно навести опис блоків, дати посилання на схему.
4.8 Опис програми
За побудованою схемою алгоритму розробити програму та дати її опис.
В описі треба указати мову програмування, обчислювальне середовище. Далі треба привести початкові та кінцеві дані, дати опис окремих блоків, використання процедур, а також стандартного програмного забезпечення, якщо воно використовується. Опис вміщує посилання на лістінг програми. До курсового проекту додається дискета з програмою.
4.9 Інструкція користувачу програми
Інструкція повинна бути написана так, щоб споживач міг вільно нею користуватись. Тому треба привести перелік необхідних дій для запуску програми, надрукувати екранні форми: головну, із початковою та кінцевою інформацією.
Похожие работы
... нашої транспортної задачі: Відповідь: розроблений план перевезень дає можливість отримати мінімальні витрати у розмірі 237,5 грошових одиниць Завдання 4 Побудувати лінійну модель регресивного аналізу для економічного показника, зміни якого спостерігалися в певному інтервалі часу. Контрольний термін 1 2 3 4 5 6 7 8 9 10 Значення показника 9 16 20 27 34 39 44 ...
... : Приведемо її до канонічної форми і доповнимо її базисами: Повернемось до заміни: x1=0 x2=6 Завдання 4. Транспортна задача Для заданих транспортних задач скласти математичну модель і розв’язати їх методом потенціалів, використавши для визначення початкового плану метод мінімального елемента або північно-західного кута. 1. ...
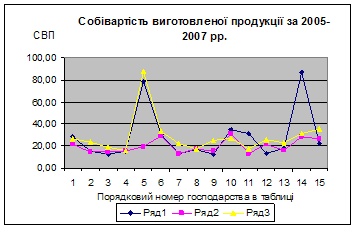
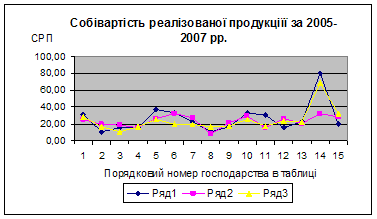
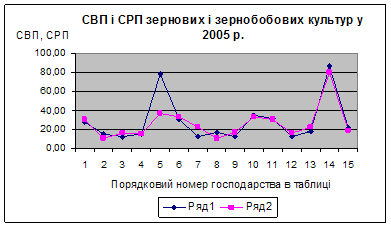
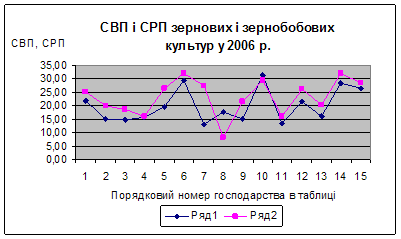
... змін, спостерігається тільки нестабільність та по деяких господарствах різкі зміни собівартості продукції, що виготовляється та реалізується. 3. Економіко-математичне моделювання в управлінні підприємством 3.1 Економіко-математичне моделювання урожайності сільськогосподарської продукції методом Брандона. Нехай економіко-математична модель матиме вид: , Де =; =; = ; Y - ...
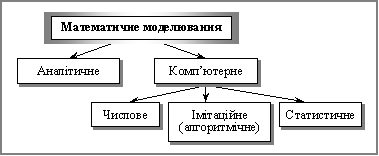
... модель, яка опосередковує відносини між об’єктом, який вивчається, та суб’єктом, який пізнає (системним аналітиком). Головним гальмом для практичного застосування математичного моделювання в економіці є проблема наповнення розроблених моделей конкретною та якісною інформацією. Точність і повнота первинної інформації, реальні можливості її збору й опрацювання справляють визначальний вплив на виб ...
0 комментариев