Навигация
Вирішення проблеми
3. Вирішення проблеми
3.1 Формулювання оптимальної задачі
Оптимальний план розподілу співвідношень продукції може бути складений за допомогою методів економіко-математичного моделювання.
Уведемо умовні позначення:
Xi - вид товарної групи (асортиментна позиція);
N - Число всіх видів товарних груп;
m- кількість місяців;
Q1, Q2 - нижня й верхня межі обсягів товарообігу для складу;
Р1і - ціна покупки одиниці товару ДП ТД «Сандора»;
Р2і - ціна реалізації одиниці товару ДП ТД «Сандора»;
k1 –прибуток, що отримує підприємтсво з одиниці прдукції;
k2 - утрата прибутку на 1 шт продукту, зумовлена відсутністю товару, попит на який перевищив замовлену кількість;
S - загальна площа складських приміщень;
S і – площа на складі, що займає і-тий вид продукції;
Параметри ящика: l - довжина; h –висота ; w – ширина.
Sод –площа, що займає одиниця продукції (ящик);
Хзаг.ск. – загальна кількість ящиків, що можуть розміщатись на складі одночасно;
Хопт – оптимальний (розрахункова) кількість товару і-того виду на складі;
Сзбі – вартість зберігання товару і –того виду;
Сзб/оді -вартість зберігання одиниці товару і –того виду;
Статистичний метод розрахунку оптимального запасу продукції базується на спостереженнях за попитом товару протягом певного часу.
На підставі цього спостереження будується емпірична функція розподілу вигляду
![]() , (3.1)
, (3.1)
де Р – імовірність того, що попит – х – буде менше наперед заданого значення Х.
Тоді оптимальний попит (Хопт) буде знайдено за оптимальним значенням цієї функції, який розраховується за
F(Хопт) = k1 / ( k1+ k2) , (3.2)
Потрібне вирішення (2) відносно (Хопт). Оскільки, частіше всього емпірична функція розподілу описується функцією виду ![]()
![]() , (3.3)
, (3.3)
де а, b – константи, рішення має вигляд
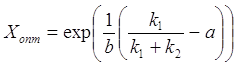 . (3.4)
. (3.4)
Торгове підприємство має обмежену площу складу (S) і номенклатуру продукції з n найменувань, які представлені на складі у кількості хі. Для кожного найменування відомо площу, яку займає одиниця продукції si (1<i<n).
В цих умовах задача стає багатокритеріальною. З одного боку потрібно, щоб прибуток
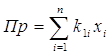 , (3.5)
, (3.5)
був максимальним. З іншого боку бажано, щоб різниця між оптимальним значенням запасу продукції і реальним
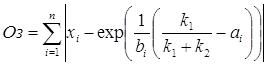 , (3.6)
, (3.6)
була б мінімальною. Знак „по модулю” означає, що відхилення хі від оптимального запасу може бути в обидва боки. Обмеженням тут виступає загальна площа складу
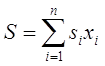 . (3.7)
. (3.7)
Для вирішення цієї задачі пропонується функціонал виду
![]() , (3.8)
, (3.8)
або
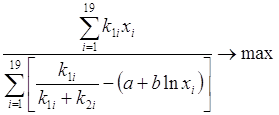 (3.9)
(3.9)
з обмеженнями на площу (загальна площа складських приміщень в цьому обмеженні множиться на 5, так як, піддони з ящиками можна ставити один на один у висоту, але не більше 5 штук.)
 , (3.10)
, (3.10)
та на ненегативні значення кількості кожного виду продукту.
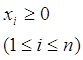 . (3.11)
. (3.11)
Введемо додаткові обмеження на верхні та нижні межі товарообігу на складі:
![]() (3.12)
(3.12)
В дипломній роботі наведено вирішення подібної задачі для торгового підприємства „Сандора”, яке має номенклатуру з 19 продуктів і обмежений склад. Емпіричні функції розподілу було розраховано за спостереженнями попиту продукту протягом 1 року.
Треба знайти оптимальне співвідношення товарів на складі по видам продукції та визначити економічний ефект від цієї оптимізації.
3.2 Визначення оптимальних співвідношень розподілу різних видів товарів на складі
На практиці, спостерігаючи за зміною значень випадкової величини, практично неможливо визначити ані закон розподілу, ані основні числові характеристики, бо невідомі ймовірності появи., того чи іншого значення. А для того, щоб їх визначити, треба проводити дуже великі спостереження, що пов`язано зі значними матеріальними затратами. Тому, замість чисельних спостережень за випадковою величиною використовується якась відносно невелика їх кількість, яка називається “вибіркою”.
Статистичні спостереження за попитом на товар кожного виду протягом одного року були зібрані шляхом відстеження заявок клієнтів на замовлення товару. З першу, початкові данні для оптимальності розрахунків та масштабування моделі були переведені з одиниць розмірності «штуки/пляшки» в «ящики». Первинні дані були отримані з даних програмного комплексу «1С підприємство»
Треба зауважити, що кожен ящик товару (незалежно від його виду) має однакові габарити, а різниться лише по кількості упаковок у ньому. Таким чином, щоб перевести кількість товару в залежності від ємності в ящики треба кількість упаковок поділити на кількість їх у ящику. Дані про кількість упаковок в ящику в залежності від виду соку наведені в табл. 3.1
Таблиця 3.1. Дані про кількість упаковок в ящику в залежності від виду соку
| Ємність упаковки, л | 0,2 | 0,5 | 1 | 1,5 |
| Кількість в ящику, шт | 18 | 18 | 12 | 8 |
Таким чином ми маємо вибірку значень випадкової величини Х= x1, x2, …. xn, з кількістю спостережень – m.
Таблиця 3.2
Вихідні дані (приклад)
| № | Асортиментна позиція | 01.05.03 | 01.06.03 | 01.07.03 | 01.08.03 | ....... | 01.07.04 | 01.08.04 | 01.09.04 | 01.10.04 | 01.11.04 | 01.12.04 |
| 1 | Вина кріплені | 135 | 220 | 308 | 308 | ....... | 328 | 324 | 258 | 205 | 186 | 7 |
| 2 | Вина сухі | 33 | 163 | 312 | 406 | ....... | 135 | 142 | 169 | 171 | 171 | 223 |
| 3 | Вина СК | 0 | 0 | 0 | 0 | ....... | 352 | 448 | 573 | 565 | 656 | 627 |
| 4 | ДАР 0,2 | 10642 | 6244 | 6923 | 6589 | ....... | 5338 | 4487 | 5480 | 5078 | 4659 | 4905 |
| 5 | ДАР 1 | 8385 | 5909 | 5833 | 5147 | ....... | 6216 | 6411 | 6622 | 7421 | 8569 | 10108 |
| 6 | ДАР 1,5 | 3047 | 2340 | 2249 | 1809 | ....... | 2160 | 2595 | 2241 | 3092 | 3582 | 5028 |
| 7 | Сандорік 0,2 | 2733 | 1471 | 2943 | 3660 | ....... | 4442 | 4039 | 3774 | 3833 | 3153 | 3507 |
| 8 | Садочок 0,2л | 5144 | 4824 | 4314 | 3856 | ....... | 11349 | 10201 | 11280 | 11460 | 11575 | 11423 |
| 9 | Садочок 0,5л | 0 | 0 | 0 | 0 | ....... | 1332 | 1196 | 1537 | 1469 | 1562 | 1812 |
| 10 | Садочок 1л | 21672 | 17513 | 11406 | 9507 | ....... | 15286 | 16754 | 18800 | 21991 | 25756 | 31597 |
| 11 | Садочок 1,5л | 1746 | 1403 | 1031 | 1152 | ....... | 2462 | 2870 | 2909 | 3090 | 3773 | 5200 |
| 12 | Соки "Українська класика"1л | 0 | 0 | 0 | 0 | ....... | 878 | 1042 | 1016 | 1415 | 1530 | 1448 |
| 13 | Соки "Фрукти світу" 1л | 0 | 0 | 0 | 243 | ....... | 517 | 654 | 579 | 649 | 780 | 775 |
| … | ………. | ……….. | ………. | ………. | ………. | ……… | ………. | ………. | ………. | ………. | ………. | ………. |
Розіб`ємо весь діапазон можливих значень спостережень випадкової величини на d ділянок. Знайдемо значення випадкової величини на правій межі кожної ділянки як
dmax(i) =xmin +(xmax – xmin)i/d, (3.13)
де, i – номер ділянки [1, d]; xmax, xmin – відповідно найбільше та найменше значення випадкової величини у вибірці. Права межа і-ї ділянки водночас є лівою межею і+1 – ї ділянки. Ліва межа для 1-ї ділянки – це xmin. А права межа d–ї ділянки – це xmax.
Орієнтовно, кількість цих ділянок може бути визначена як
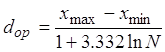 .(3.14)
.(3.14)
Таблиця3.3Визначення меж та кількості інтервалів
| хі мин | хі макс | Теоретична кількість діапазонів | Практична кількість інтервалів | Крок | Розрахунок правої межі інтервалів | |||||||
| 7 | 328 | 29 | 8 | 40 | 47 | 88 | 128 | 168 | 208 | 248 | 288 | 328 |
| 29 | 406 | 34 | 47 | 76 | 124 | 171 | 218 | 265 | 312 | 359 | 406 | |
| 0 | 656 | 60 | 82 | 82 | 164 | 246 | 328 | 410 | 492 | 574 | 656 | |
| 2520 | 10642 | 740 | 1015 | 3535 | 4550 | 5566 | 6581 | 7596 | 8611 | 9626 | 10642 | |
| 4820 | 11337 | 593 | 815 | 5635 | 6449 | 7264 | 8079 | 8893 | 9708 | 10523 | 11337 | |
| 1809 | 5028 | 293 | 402 | 2211 | 2613 | 3016 | 3418 | 3821 | 4223 | 4626 | 5028 | |
| 1471 | 5044 | 325 | 447 | 1918 | 2364 | 2811 | 3257 | 3704 | 4151 | 4597 | 5044 | |
| 3415 | 11575 | 743 | 1020 | 4435 | 5455 | 6475 | 7495 | 8515 | 9535 | 10555 | 11575 | |
| 0 | 1812 | 165 | 226 | 226 | 453 | 679 | 906 | 1132 | 1359 | 1585 | 1812 | |
| 9507 | 31597 | 2012 | 2761 | 12268 | 15029 | 17790 | 20552 | 23313 | 26074 | 28835 | 31597 | |
| 1031 | 5200 | 380 | 521 | 1552 | 2074 | 2595 | 3116 | 3637 | 4158 | 4679 | 5200 | |
| 0 | 3231 | 294 | 404 | 404 | 808 | 1212 | 1615 | 2019 | 2423 | 2827 | 3231 | |
| 0 | 994 | 91 | 124 | 124 | 248 | 373 | 497 | 621 | 745 | 870 | 994 | |
| 3066 | 6415 | 305 | 419 | 3485 | 3903 | 4322 | 4740 | 5159 | 5578 | 5996 | 6415 | |
| 1000 | 3981 | 271 | 373 | 1373 | 1745 | 2118 | 2490 | 2863 | 3236 | 3608 | 3981 | |
| 5418 | 13778 | 761 | 1045 | 6463 | 7508 | 8553 | 9598 | 10643 | 11688 | 12733 | 13778 | |
| 2904 | 8517 | 511 | 702 | 3606 | 4308 | 5009 | 5711 | 6412 | 7114 | 7816 | 8517 | |
| 0 | 747 | 68 | 93 | 93 | 187 | 280 | 373 | 467 | 560 | 653 | 747 | |
| 0 | 157 | 14 | 20 | 20 | 39 | 59 | 79 | 98 | 118 | 138 | 157 | |
Результати розбивки на інтервали можна побачити в табл. 3.3.
Визначимо кількість значень випадкової величини, що попали в ту чи іншу ділянку як Кі. Це число називається “частотою”. “Відносною частотою” називається число
kі= Кі / N. (3.15)
Відкладемо по осі абсцис значення випадкової величини Х, розділивши ці значення на діапазони згідно (3.14).
По осі ординат відкладемо для кожного діапазону значення частоти або відносної частоти у вигляді горизонтальної лінії для кожного діапазону.
Таблиця 3.4. Визначення частот та кармнів числових характеристик
| Карман | Частота | Відносна частота | Кумулята |
| 7 | 1 | 0,05 | 0 |
| 47 | 2 | 0,1 | 0,05 |
| 88 | 1 | 0,05 | 0,15 |
| 128 | 6 | 0,3 | 0,2 |
| 168 | 4 | 0,2 | 0,5 |
| 208 | 1 | 0,05 | 0,7 |
| 248 | 1 | 0,05 | 0,75 |
| 288 | 4 | 0,2 | 0,8 |
| 328 | 0 | 0 | 1 |
Ми отримаємо графік, що називається “гістограма” . Цей графік має широке застосування в математичній статистиці і частково заміняє собою функцію щільності розподілу, але не є її повним еквівалентом.
Наступним кроком виконаємо експоненційне сгладження данних для кожного виду товару. Графік, який ми при цьому отримуємо показан на рис. 3.1.
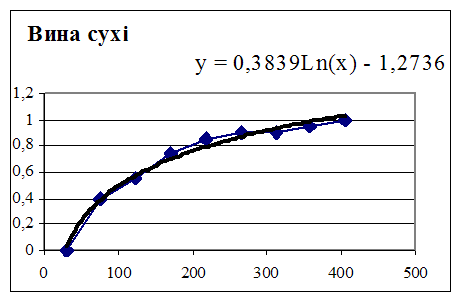 |
Рис. 3.1. – Експоненційне сгладжування емпіричної функції попиту на сухі вина.
Для цього додамо до графіку попиту на кожний товар лінію тренду. Задамо логарифмічних його тип та в параметрах вкажемо “Показувати рівняння на діаграмі”. Таким чином ми отримуємо рівняння попиту на кожен вид товару. Це рівняння виду ![]() . Для зручності зведемо всі коефіцієнти в одну таблицю.
. Для зручності зведемо всі коефіцієнти в одну таблицю.
Таблиця 3.5. Таблиця коефіцієнтів експоненційного з гладження функцій розподілу попиту на окремі види товару.
| № | А | в | |
| 1 | Вина кріплені | 0,25 | -0,74 |
| 2 | Вина сухі | 0,38 | -1,27 |
| 3 | Вина СК | 0,08 | -0,012 |
| 4 | ДАР 0,2 | 0,83 | -6,6 |
| 5 | ДАР 1 | 1,24 | -10,57 |
| 6 | ДАР 1,5 | 1 | -7,55 |
| 7 | Сандорік 0,2 | 0,83 | -6,29 |
| 8 | Садочок 0,2л | 0,58 | -4,7 |
| 9 | Садочок 0,5л | 2,38 | -16,9 |
| 10 | Садочок 1л | 0,93 | -8,21 |
| 11 | Садочок 1,5л | 0,65 | -4,81 |
| 12 | Соки "Українська класика"1л | -0,73 | -4,89 |
| 13 | Соки "Фрукти світу" 1л | 0,19 | -6,79 |
| 14 | Соки Класик 1л | 1,35 | -10,31 |
| 15 | Соки Gold 1,5л | 0,77 | -5,72 |
| 16 | Соки Gold 1л | 1,12 | -10,07 |
| 17 | Соки Gold 0,25л | 1,02 | -7,88 |
| 18 | Напої 0,2 | 0,22 | -0,49 |
| 19 | Напої 1 | 0,24 | -0,61 |
Далі на основі фінансової діяльності підприємства отпимуємо наступні вхідні дані для моделі :
Ціна купівлі ДП ТД “Сандора”1 ящика по всім видам товару;
Ціна реалізації ДП ТД “Сандора”1 ящика по всім видам товару;
Собівартість плюс додаткові витрати на зберігання 1 шт продукту, який не був проданий у встановлений час, оскільки попит на нього виявився меншим від того, що прогнозується;
Всі вони представлені в табл. 3.6.
Наступним кроком треба задати такі входи моделі, як параметри складських приміщень. А саме:
Параметри ящика (довжина, висота та ширина);
Загальна (корисна) площа складських приміщень;
Таблиця 3.6. Вихідні параметри для розрахунків
| Асортиментна позиція | Р1, купівля грн./ящ | Р2, реалізація грн./ящ | різниця (P2-P1) | вартість збер 1 прод, грн,К1і |
| Хі | P2i | P1i | К1і | К2і |
| Вина кріплені | 53,55 | 76,5 | 22,95 | 0,123843 |
| Вина сухі | 45,976 | 65,68 | 19,704 | 0,126456 |
| Вина СК | 57,75 | 82,5 | 24,75 | 0,132832 |
| ДАР 0,2 | 19,845 | 28,35 | 8,505 | 0,126247 |
| ДАР 1 | 27,09 | 38,7 | 11,61 | 0,121092 |
| ДАР 1,5 | 29,904 | 42,72 | 12,816 | 0,120032 |
| Сандорік 0,2 | 7,98 | 11,4 | 3,42 | 0,139613 |
| Садочок 0,2л | 16,443 | 23,49 | 7,047 | 0,126655 |
| Садочок 0,5л | 21,546 | 30,78 | 9,234 | 0,125369 |
| Садочок 1л | 24,696 | 35,28 | 10,584 | 0,12776 |
| Садочок 1,5л | 24,192 | 34,56 | 10,368 | 0,1386 |
| Соки "Українська класика"1л | 26,46 | 37,8 | 11,34 | 0,131859 |
| Соки "Фрукти світу" 1л | 65,45 | 93,5 | 28,05 | 0,128713 |
| Соки Classic 1л | 27,216 | 38,88 | 11,664 | 0,128687 |
| Соки Gold 1,5л | 33,6 | 48 | 14,4 | 0,124837 |
| Соки Gold 1л | 36,036 | 51,48 | 15,444 | 0,134996 |
| Соки Gold 0,2л | 17,01 | 24,3 | 7,29 | 0,127348 |
| Напої 0,2 | 16,443 | 23,49 | 7,047 | 0,131725 |
| Напої 1 | 23,94 | 34,2 | 10,26 | 0,130286 |
Ціна оренди 1 м2 складських площ.
В даному прикладі були використані вихідні дані, представлені в табл. 3.7
Таблиця 3.7 Параметри складу
| Площа складу, м2 | Ціна оренди 1 м2 за міс, грн/м2 | Загальна вартість зберігання прод.,грн на міс | пл. 1шт | кіл.шт на складі | Параметри ящика, м | ||
| S | Ps1 | Ps | S од тов | Q склад | Довж | шир | вис |
| 6490 | 4 | 25960 | 0,315 | 20603,17 | 0,7 | 0,45 | 0,35 |
При цьому такі показники , як загальна вартість зберігання продукції на складі, площа одного ящика товару та кількість товару на складі розраховується системою автоматично.
Обмеження, що постали при розв’язанні цієї задачі були наступні:
Максимальні обсяги виробництва продуктів (допускається нарощування підприємством виробничих потужностей не більше ніж на 50% від існуючих обсягів виробництва)
Мінімальні обсяги реалізації товару по кожному виду (це значить, що головною компанією обумовлюються визначені нормативи товарів по кожному виду, для зберігання певних цінових та цільових сегментів на ринку даної області.)
Загальна площа складу, що може бути оптимально розподілена під товари становить реальну (корисну площу складу помножену на 5. Це зумовлено можливістю ставити та зберігати піддони з соковою продукцією один на інший в висоту, але не більше 5 штук. Не пошкоджуючи продукцію.)
Невід’ємне значення кількості товарних одиниць .
Далі за допомогою надбудови Пошук рішення в MS Excel знаходимо співвідношення товарів на складі, використовуючи посилання на осередки з коефіцієнтами - параметрами експоненціального сгладжування та параметрів к1 і к2. Для вищеозначених вхідних даних були отримані наступні результати – дивись табл. 3.8
Таблиця 3.8. Отримані результати оптимізації
| Кільк. прод. по видам | Вартість зберіг. по видам (чис) | Відх від опт розпод пл (знаменник цільової функції) | Приб від реал за міс по видам в сер, грн | обмеження по кільк. кожного виду,min | обмеження по кільк. кожного виду,max | пл. під вид м2 |
| Хі* | С зб | Q1 | Q2 | Si | ||
| 271 | 33,50965 | 3,899790849 | 6 210 | 90 | 271 | 85 |
| 64 | 8,112666 | 4,91121393 | 1 264 | 64 | 192 | 20 |
| 242 | 32,09639 | 0,008812743 | 5 980 | 81 | 242 | 76 |
| 8822 | 1113,71 | 59,14539987 | 75 028 | 2 941 | 8 822 | 2779 |
| 11202 | 1356,502 | 97,32366282 | 130 059 | 3 734 | 11 202 | 3529 |
| 4564 | 547,7766 | 62,62454422 | 58 487 | 1 521 | 4 564 | 1438 |
| 5662 | 790,5097 | 53,56461804 | 19 365 | 1 887 | 5 662 | 1784 |
| 11686 | 1480,043 | 43,45839816 | 82 349 | 3 895 | 11 686 | 3681 |
| 266 | 33,30775 | 91,97395408 | 2 453 | 266 | 797 | 84 |
| 18263 | 2333,22 | 79,64343986 | 193 291 | 6 088 | 18 263 | 5753 |
| 5947 | 824,3076 | 41,16548638 | 61 662 | 1 982 | 5 947 | 1873 |
| 1452 | 191,4617 | 36,34416656 | 16 466 | 484 | 1 452 | 457 |
| 814 | 104,7604 | 45,32009657 | 22 830 | 271 | 814 | 256 |
| 4527 | 582,619 | 85,44953611 | 52 808 | 1 509 | 4 527 | 1426 |
| 4850 | 605,4293 | 47,78242196 | 69 836 | 1 617 | 4 850 | 1528 |
| 18449 | 2490,596 | 97,80412142 | 284 932 | 6 150 | 18 449 | 5812 |
| 5566 | 708,7644 | 66,95710858 | 40 573 | 1 855 | 5 566 | 1753 |
| 199 | 26,23908 | 2,392550695 | 1 404 | 66 | 199 | 63 |
| 18 | 2,31474 | 1,527706835 | 182 | 18 | 53 | 6 |
| 102862,3 | 13265,28 | 921,2970297 | 1 125 179 | 34 519 | 103 558 | 32 402 |
Значення цільової функції при цьому склало 14,3984.
3.3 Визначення економічного ефекту від запровадження пропозицій
Таки чином, оптимізувавши кількість товару кожного виду на складі було отримано максимальне значення прибутку (при умові дотримання даних обмежень). Його величина склала 1 125 179 грн. До оптимізації асортименту товарів ця величина була 755 319 грн. Економічний ефект від оптимізації становить 369 860 грн. (див. табл. 3.9).Із таблиці видно, що дані заходи привели до збільшення загального виторгу підприємства майже на 50% і становлять 1 232 868 грн., з величини 2 517 730 грн. до 3 750 598 грн.
Табл. 3.9. Загальний економічний ефект від впровадження оптимізації
| Виручка при неоптимальному запасі товарів, грн | 2 517 730 | Прибуток при неоптимальному запасі товару, грн | 755 319 |
| Виручка приоптимальному запасі товарів, грн | 3 750 598 | Прибуток при оптимальному запасі товару, грн | 1 125 179 |
| Економічний ефект | 1 232 868 | Економічний ефект | 369 860 |
Економічний ефект від оптимізації збільшив прибуток фірми на 369 806 грн. Величина приросту становить майже 50% (з величини 755 319 до 1 125 179 грн.)
Результати та наслідки оптимізації по кожному виду продукції наведені в табл. 3.10.
До основних моментів можна віднести :
Помилкове рішення менеджерів компанії про зняття з виробництва таких асортиментних позицій як Напої ємністю 0,2 л та Напої ємністю 1 л. Хоча по позиції Напої 1л треба зменшити масштаби запасів вдвоє з 36 до кількості 18 ящиків. А ось запаси по даній позиції ємністю 0,2 л треба збільшити майже в два рази до величини 199 ящиків. Прибуток по ним склав 182 грн. та 1 404 грн. відповідно.
Зменшення запасів по сухим винам майже на 50% до величини 64 ящика. При цьому має місце пропорційне зменшення прибутку по цій позиції, але не зважаючи на це – загальний прибуток підприємства збільшується.
Аналогічно попередній спостерігається ситуація з соками Садочок 0,5 л. Зменшення на 266 ящиків (що становить 50 %)
Приводить до зменшення прибутку, що отримується за рахунок даного виду товару, з 4 907грн. до 2 453 грн.
4. Максимальні питому вагу в структурі прибутків займають такі позиції:
соки gold 1 л., Садочок 1 л. та Дар 1л. Їх величини становлять 284 932 грн., 193 291 грн. та 130 059 грн. відповідно.
Мінімальну займає Напої 1л, яка має величину в гривневому еквіваленті всього 182 грн.
Табл. 3.10 Результати оптимізації по кожному виду товару
| Асортиментна позиція | Середнє значення кількості проданих ящиків за видами за місяць, ящики | Оптимальне (розраховане) середнє значення кількості проданих ящиків за видами за місяць, ящики | Відхилення | Величина виторгу не оптимізована | Величина виторгу оптимізована | Прибуток не оптимізований | Прибуток оптимізований |
| |
| Хі | Хі* | (Хі*-Хі) | Хі*Р2 | Хі**Р2 | (Р2-Р1)*Хі | (Р2-Р1)*Хі* | |||
| 1 | Вина кріплені | 180 | 271 | 90 | 13 800 | 20 699 | 4 140 | 6 210 |
|
| 2 | Вина сухі | 128 | 64 | -64 | 8 427 | 4 214 | 2 528 | 1 264 |
|
| 3 | Вина СК | 161 | 242 | 81 | 13 290 | 19 935 | 3 987 | 5 980 |
|
| 4 | ДАР 0,2 | 5 881 | 8 822 | 2 941 | 166 729 | 250 094 | 50 019 | 75 028 |
|
| 5 | ДАР 1 | 7 468 | 11 202 | 3 734 | 289 019 | 433 529 | 86 706 | 130 059 |
|
| 6 | ДАР 1,5 | 3 042 | 4 564 | 1 521 | 129 971 | 194 956 | 38 991 | 58 487 |
|
| 7 | Сандорик 0,2 | 3 775 | 5 662 | 1 887 | 43 032 | 64 548 | 12 910 | 19 365 |
|
| 8 | Садочок 0,2л | 7 790 | 11 686 | 3 895 | 182 997 | 274 496 | 54 899 | 82 349 |
|
| 9 | Садочок 0,5л | 531 | 266 | -266 | 16 355 | 8 178 | 4 907 | 2 453 |
|
| 10 | Садочок 1л | 12 175 | 18 263 | 6 088 | 429 535 | 644 303 | 128 861 | 193 291 |
|
| 11 | Садочок 1,5л | 3 965 | 5 947 | 1 982 | 137 028 | 205 541 | 41 108 | 61 662 |
|
| 12 | Соки "Українська класика"1л | 968 | 1 452 | 484 | 36 591 | 54 886 | 10 977 | 16 466 |
|
| 13 | Соки "Фрукти світу" 1л | 543 | 814 | 271 | 50 733 | 76 100 | 15 220 | 22 830 |
|
| 14 | Соки Classic 1л | 3 018 | 4 527 | 1 509 | 117 351 | 176 026 | 35 205 | 52 808 |
|
| 15 | Соки Gold 1,5л | 3 233 | 4 850 | 1 617 | 155 192 | 232 788 | 46 558 | 69 836 |
|
| 16 | Соки Gold 1л | 12 300 | 18 449 | 6 150 | 633 183 | 949 774 | 189 955 | 284 932 |
|
| 17 | Соки Gold 0,25л | 3 710 | 5 566 | 1 855 | 90 163 | 135 244 | 27 049 | 40 573 |
|
| 18 | Напої 0,2 | 133 | 199 | 66 | 3 119 | 4 679 | 936 | 1 404 |
|
| 19 | Напої 1 | 36 | 18 | -18 | 1 215 | 608 | 365 | 182 |
|
4. Опис Інформаційної системи
4.1 Вступ
АІС для управління запасами на складі роздрібного підприємства призначена для вирішення задачі „Розрахунок оптимального запасу продукції для отримання максимального прибутку з урахуванням обмеження площі складських приміщень ТД ДП „Сандора”.
Вона виконує автоматизований розрахунок оптимального співвідношення товарів по асортименту на складі при даних обмеженнях складських приміщень з ціллю максимізувати величину прибутку, що отримує підприємство.
Структурна схема Інформаційної системи АІС-Оптимальний запас надається у Додатку „Структурна схема Інформаційної системи «АІС-Оптимальний запас».
Для проведення розрахунків на персональному комп'ютері повинна бути установлена операційна система Windows 98 або більш пізніша система.
Похожие работы
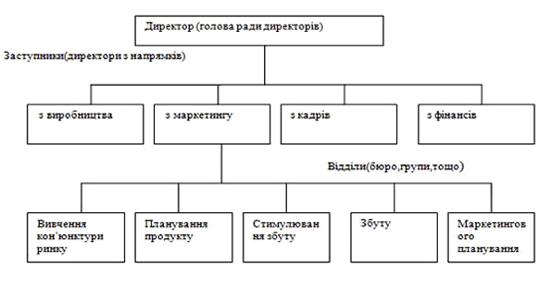
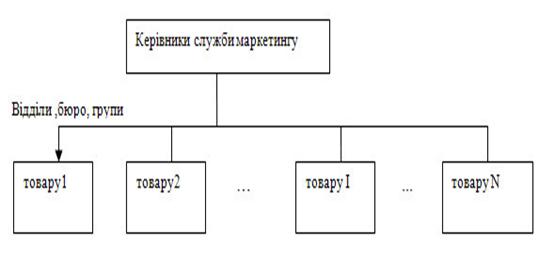
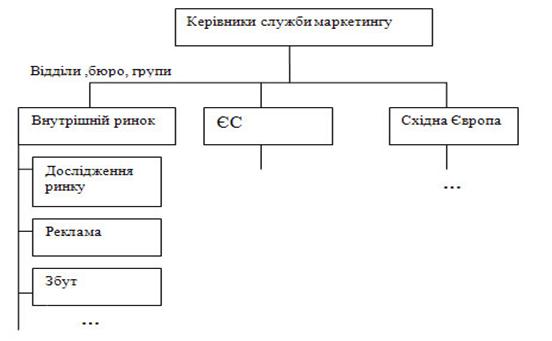
... усі ті слабкі сторони, котрі притаманні окремим підструктурам, що включені в єдину комбіновану структуру організації маркетингової діяльності підприємства. [7;5;26.]. Розглянувши всі види організації служби маркетингу і досліджуване нами підприємство, можна зробити висновок, що ТМ «Смак» працює за сигментной побудовою організації служби маркетингу, що веде до великих затрат коштів.Так як пі ...
... Чарка, стакан 4 320 2 80 400 Столові прибори (комплект) 4 320 2 80 400 Далі наведемо характеристику посуду, який будуть використовувати в комплексному закладі ресторанного господарства (табл. 2.8–2.11). Таблиця 2.8. Характеристика та призначення класичного вітчизняного порцелянового та фаянсового посуду Найменування Розміри, мм Місткість, см3, порцій Призначення ...
... дослідний зразок вина. Мікробіологічним аналізом визначають стан мікрофлори, природу помутніння і осаду. 3. Дослідницько – аналітична частина 3.1 Соціально – економічні аспекти ринку виноградних вин в Україні Вирощування виноградної лози та виробництво виноробної продукції зосереджено в країнах з помірним і субтропічним кліматом, точніше на території між 30 і 500 північної широти, в ...


0 комментариев