Реалізовувати шляхом оптової, роздрібної, комісійної та іншої, в тому числі посередницької торгівлі соки, алкогольні та безалкогольні напоїв;
Економічний аналіз результатів діяльності ДП ТД «Сандора»
Фінансові результати
Аналіз майнового стану підприємства
Коефіцієнт оборотності основних засобів
Теоретичні основи оптимальних розрахунків
Використання моделей на різних рівнях керування
Оптимізаційні моделі
Обмеження
Вирішення проблеми
Структура розрахунків
Програмне забезпечення
Заходи, що проводяться на ДП ТД «Сандора» для попередження травматизму та забезпечення нормальних умов життєдіяльності
Медичні огляди
Розслідування й облік нещасних випадків
Заходи по створенню безпечних та здорових умов праці
Характеристика приміщення за вибухо- та пожежною небезпекою
Навигация
Оптимізаційні моделі
Оптимальне використання складських приміщень на ТД ДП "Сандора"
161859
знаков
21
таблица
7
изображений
2.5 Оптимізаційні моделі
Кількісні моделі прийняття рішеньзадають зв'язки між змінними рішення і параметрами і обчислює показник ефективності (прибуток), а також результуючі змінні (значення обмежених ресурсів).
Модель являє типовий приклад задачі умовної оптимізації: необхідно максимізувати (мінімізувати) якийсь показник ефективності, що залежить від змінних рішень, які, у свою чергу, підкоряються ряду обмежень. Обмеження звужують діапазон припустимих рішень. У даному конкретному випадку обмеження - це кількість різних деталей, з яких можна виготовляти стільці, однак існує багато інших типів обмежень. Як правило, менеджерові доводиться приймати більшу частину рішень в умовах, коли припустимі рішення тим або іншим способом обмежені. У своєму приватному житті ми також часто зіштовхуємося з обмеженнями - з недостачею часу, грошей, простору або сил. Менеджер повинен брати до уваги вимоги до капіталовкладень, наявність персоналу, графік поставок комплектуючих, квоти на імпорт, вимоги профспілок виробничі можливості заводу, вимоги по охороні навколишнього середовища, витрати на зберігання, вимоги законодавства й множина інших факторів. Тому немає нічого дивного в тому, що умовна оптимізація досягнення найкращого можливого результату при наявності існуючих обмежень є одним з найбільше що активно розвиваються напрямків досліджень у науці керування.
2.5.1 Чисельні методи безумовної оптимізації
Безумовною оптимізацією називається рішення задачі нелінійного програмування, що не містить обмеження:
f (x1, x2,…,xn)®extr (2.1)
У певних випадках для рішення подібних задач доцільно використати чисельні методи. Чисельні методи мають наступні особливості:
вони орієнтовані на застосування ЕВМ і допускають великий об'єм однотипних обчислень;
дозволяють одержати наближене рішення з наперед заданою точністю;
містять ітераційні співвідношення.
f (Х0) > f (Х1) >…>f (Хk) >… (2.2)
Процес рішення задачі (2.1) чисельним методом виконується поетапно. Кожен такий етап (або ітерація) дозволяє перейти в нову крапку в n-мірному просторі Х= (x1, x2,…,xn)... Для такого ітераційного процесу необхідне виконання співвідношень:
при пошуку мінімуму функції f (Х). Тут k - номер ітерації. Далі для визначеності будемо розглядати задачі на пошук мінімуму функції.
2.5.1.1 Градієнтний метод із дробленням кроку
Вихідні дані: f (x1, x2,…,xn)– функція n змінних;
Х0 (x10, x20,…,xn0)– координати початкової крапки;
a - початкове значення кроку;
e- точність обчислень.
Обчислення виконуються по кроках:
Обчислюється значення функції в черговій крапці f (xC).
Обчислюються координати наступної крапки:
(2.3)
Якщо f (Х i+1)> f (Х i ), то треба зменшивши вдвічі a, повторити обчислення п. 2.
Перевіряється умова досягнення точності:
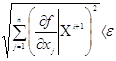(2.4)
Якщо точність не досягнута, переходять до п. 2.
2.5.1.2 Метод найшвидшого спуска
|
f (Х i+1)= f [ Х i – agrad f (Х i )]Õ (2.5)
Незважаючи на додаткові обчислення на кожній ітерації цей метод забезпечує швидкий вихід в область екстремуму.
Вихідні дані: f (x1, x2,…,xn)– функція n змінних;
Х0 (x10, x20,…,xn0)– координати початкової крапки;
e- точність обчислень.
Кожна ітерація включає наступні дії:
Обчислюються складового вектора градієнта в черговій i-ої крапці.
|
Визначаються координати чергової крапки:
(2.6)
Якщо умова
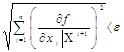
не виконується, то переходять до п. 2.
2.6 Лінійне програмування
Існують ефективні методи пошуку рішень для моделей оптимізації з лінійними обмеженнями. Моделі з лінійними обмеженнями називаються моделями лінійного програмування (ЛП). Однак, перш ніж перейти безпосередньо до процесу оптимізації моделей, варто приділити увага поданню моделей ЛП в електронних таблицях. У цій главі ми розглянемо: 1) методику формалізації моделей ЛП; 2) правила подання моделей ЛП в електронних таблицях, які спростять застосування засобу Excel Пошук рішення; 3) використання засобу Пошук рішення для оптимізації моделей ЛП.
Похожие работы
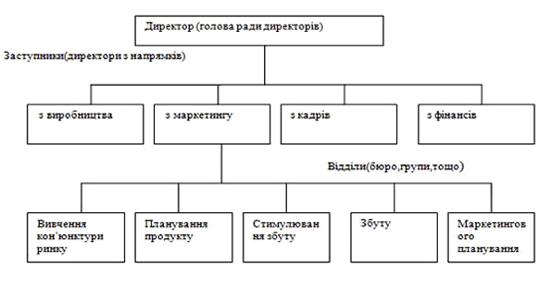
... усі ті слабкі сторони, котрі притаманні окремим підструктурам, що включені в єдину комбіновану структуру організації маркетингової діяльності підприємства. [7;5;26.]. Розглянувши всі види організації служби маркетингу і досліджуване нами підприємство, можна зробити висновок, що ТМ «Смак» працює за сигментной побудовою організації служби маркетингу, що веде до великих затрат коштів.Так як пі ...
... Чарка, стакан 4 320 2 80 400 Столові прибори (комплект) 4 320 2 80 400 Далі наведемо характеристику посуду, який будуть використовувати в комплексному закладі ресторанного господарства (табл. 2.8–2.11). Таблиця 2.8. Характеристика та призначення класичного вітчизняного порцелянового та фаянсового посуду Найменування Розміри, мм Місткість, см3, порцій Призначення ...
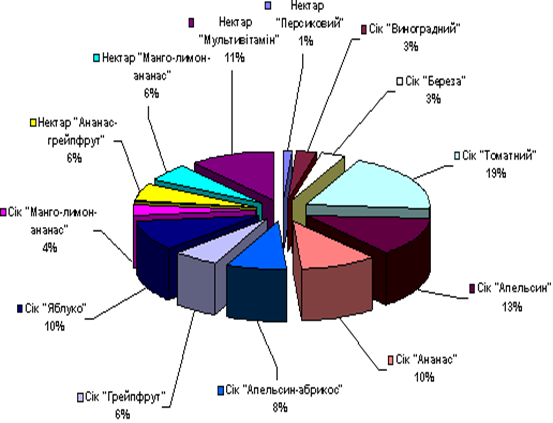
... дослідний зразок вина. Мікробіологічним аналізом визначають стан мікрофлори, природу помутніння і осаду. 3. Дослідницько – аналітична частина 3.1 Соціально – економічні аспекти ринку виноградних вин в Україні Вирощування виноградної лози та виробництво виноробної продукції зосереджено в країнах з помірним і субтропічним кліматом, точніше на території між 30 і 500 північної широти, в ...
0 комментариев