Навигация
3 Гладкая оптимизация.
Метод множителей Лагранжа позволяет отыскивать максимум или минимум функции при ограничениях-равенствах. Основная идея метода состоит в переходе от задачи на условный экстремум к задаче отыскания безусловного экстремума некоторой построенной функции Лагранжа. Пусть задана задача НП при ограничениях-равенствах вида
минимизировать 
при ограничениях
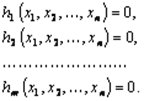
Предположим, что все функции 
– дифференцируемы. Введем набор переменных 
(число которых равняется числу ограничений), которые называются множителями Лагранжа, и составим функцию Лагранжа такого вида:
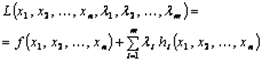
Справедливо такое утверждение для того чтобы вектор 
являлся решением задачи при ограничениях необходимо, чтобы существовал такой вектор 
, что пара векторов удовлетворяла бы системе уравнений
множителей Лагранжа, который состоит из следующих шагов.
Составляют функцию Лагранжа 
Находят частные производные 
Решают систему уравнений
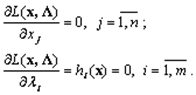
и отыскивают точки 
, удовлетворяющие системе.
Найденные точки 
дальше исследуют на максимум (или минимум).
Седловая точка и задача нелинейного программирования
Рассмотрим функцию Лагранжа 
Определение Пара векторов 
называется седловой точкой функции Лагранжа 
, если при всех 
выполняется условие
Неравенство называют неравенством для седловой точки. Очевидно, что в седловой точке выполняется условие
Между понятием седловой точки функции Лагранжа 
и решением задачи НП существует взаимосвязь, которая устанавливается в следующей теореме.
Теорема. Пусть 
и все 
выпуклы и функции 
удовлетворяют условию регулярности Слейтера. Вектор 
является решением задачи НП тогда и только тогда, когда существует такой вектор 
, что
Теорема Куна-Таккера. Пусть функции 
, имеют непрерывные частные производные на некотором открытом множестве 
, содержащем точку 
. Если 
является точкой минимума функции 
при ограничениях 
, удовлетворяющих условию регулярности в виде линейной независимости векторов 
, то существуют такие неотрицательные множители Лагранжа 
, что
Определим функцию Лагранжа следующим образом:
Тогда теорему Куна-Таккера можно записать в виде
Заметим, что множители Лагранжа 
в задаче НП с ограничениями-равенствами являются знаконеопределенными, тогда как в теореме Куна-Таккера они должны быть положительными.
Каждой задаче линейного программирования соответствует двойственная задача. Двойственная задача по отношению к исходной задаче строится по следующим правилам:
· Если исходная задача ставится на максимум, то двойственная ставится на минимум и наоборот.
· Коэффициенты целевой функции исходной задачи становятся правыми частями ограничений двойственной задачи. Правые части ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи.
· Если A-матрица коэффициентов исходной задачи, то транспонированная матрица T A будет матрицей коэффициентов двойственной задачи.
· В задаче на максимум все ограничения имеют знак ≤ (=), а в задаче на минимум все ограничения имеют знак ≥ .
· Число переменных в двойственной задаче равно числу ограничений в исходной задаче. Каждому ограничению исходной задачи соответствует переменная двойственной задачи. Если ограничение исходной задач имеет знак (≥ ), то соответствующая переменная двойственной задачи неотрицательна. Если ограничение имеет знак (=), то соответствующая переменная двойственной задачи может принимать положительные и отрицательные значения и наоборот.
Похожие работы
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
... во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные. 2. Области применения и ограничения использования линейного программирования для решения экономических задач Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление ...
... управления, прочие системы. Целью данной курсовой работы является рассмотрение, освещение и оценка возможностей пакета прикладных программ MS OFFICE с точки зрения информационных технологий и методов их использования при решении экономических задач. 2. Использование пакета прикладных программ MS OFFICE при решении экономических задач 2.1 Обзор возможностей Microsoft Office Пакет ...
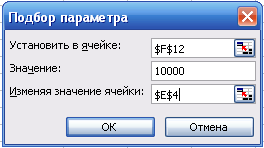
... (нынешняя) стоимость или общая сумма, которая на настоящий равноценна серии будущих выплат; Тип - 0 или 1, Если 0 – оплата производится в конце периода, если 1, то в начале. В данной задаче функции приобретают вид ЧПС(0;D2;E2;F2) и БС(I2;B2;;-C2). 4. С помощью функции Подбор параметра определена ставка, при которой выгоднее деньги вложить в инвестиционный проект 8,5%. 1. Внесены исходные ...
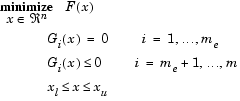
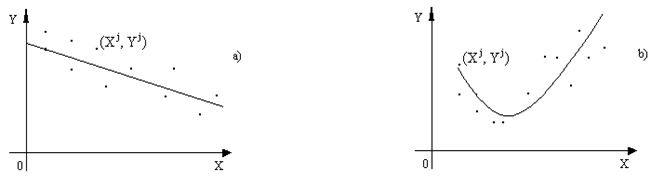
0 комментариев