Навигация
Многокритериальная оптимизация. Методы сведения многокритериальной задачи к однокритериальной
23385
знаков
0
таблиц
0
изображений
2 Многокритериальная оптимизация. Методы сведения многокритериальной задачи к однокритериальной.
Многокритериальная оптимизация представляет собой минимизацию некого вектора целей F(x), на которой могут быть наложены дополнительные ограничения или предельные значения
Отметим, что поскольку F(x) является неким вектором, то любые компоненты F(x) являюся конкурирующими и отсутсвует некое единое решение поставленной задачи. Взамен этого, для описания характеристик целей вводится концепция множества точек неулучшаемых решений (так называемая оптимальность по Парето).Неухудшаемое решение есть такое решение, в котором улучшение в одной из целей приводит к некому ослаблению другой. Для более точной формулировки данной концепции рассмотрим некую область допустимых решений 
в параметрическом пространстве 
, которое удовлетворяет всем принятым ограничениям.
Отсюда возможно определить соответствующую область допустимых решений для пространства целевых функций 
.
, где 
при условии 
Определение. Точка 
является неулучшаемым решением, если для некоторой окрестности 
нет некого 
такого, что 
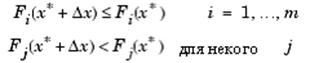
Стратегия взвешенных сумм
Данная стратегия взвешенных сумм преобразует многокритериальную задачу минимизации вектора 
в некую скалярную задачу путем построения неких взвешенных сумм для всех выбранных объектов.
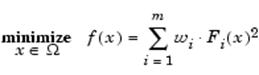
Далее уже к данной задаче оптимизации уже может быть применен стандартный алгоритм оптимизации без наличия ограничений. В этом случае рассматриваются взвешенные коэффициенты для каждой из выбранных целей. Взвешенные коэффициенты необязательно должны напрямую соответствовать относительной значимости соответствующей цели или принимать во внимание взаимовлияние между конкретно выбранными целями. Более того, границы неулучшаемых решений могут быть и не достигнуты, так что определенные решения являются по существу недостижимыми.
Метод 
-ограничений
Некий определенный способ, который отчасти позволяет преодолеть проблему выпуклости метода взвешенных сумм, есть метод 
-ограничений. В этом случае осуществляется минимизация основной цели 
и при представлении остальных целей в форме ограничений типа неравенств.
при выполнении условия
Подобный подход позволяет определить некое количество неулучшаемых решений для случая вогнутой границы, что, по существу, является недоступным в методе взвешенных сумм, например, в точке искомого решения 
и 
. Однако проблемой данного метода является подходящий выбор , который мог бы гарантировать допустимость некого решения.
Метод достижения цели
Описанный далее метод представляет собой метод достижения цели Гембики. Данный метод включает в себя выражение для множества намерений разработчика 
, которое связано с множеством целей 
. Такая формулировка задачи допускает, что цели могут быть или недо- или передостижимыми, и что дает разработчику возможность относительно точно выразить исходные намерения. Относительная степень недо- или передостижимости поставленных намерений контролируется посредством вектора взвешенных коэффициентов 
и может быть представлена как стандартная задача оптимизации с помощью следующей формулировки
При условии, что
Член 
вносит в данную задачу элемент ослабления, что, иначе говоря, обозначает жесткость заданного намерения. Весовой вектор w дает исследователю возможность достаточно точно выразить меру взаимосвязи между двумя целями. Например, установка весового вектора w как равного исходному намерению указывает на то, что достигнут тот же самый процент недо- или передостижимости цели 
. Посредством установки в ноль отдельного весового коэффициента (т.е. 
) можно внести жесткие ограничения в поставленную задачу. Метод достижения цели обеспечивает подходящую интуитивную интерпретацию поставленной исследовательской задачи и которая, в свою очередь, является вполне разрешимой с помощью стандартных процедур оптимизации.
Похожие работы
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
... во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные. 2. Области применения и ограничения использования линейного программирования для решения экономических задач Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление ...
... управления, прочие системы. Целью данной курсовой работы является рассмотрение, освещение и оценка возможностей пакета прикладных программ MS OFFICE с точки зрения информационных технологий и методов их использования при решении экономических задач. 2. Использование пакета прикладных программ MS OFFICE при решении экономических задач 2.1 Обзор возможностей Microsoft Office Пакет ...
... (нынешняя) стоимость или общая сумма, которая на настоящий равноценна серии будущих выплат; Тип - 0 или 1, Если 0 – оплата производится в конце периода, если 1, то в начале. В данной задаче функции приобретают вид ЧПС(0;D2;E2;F2) и БС(I2;B2;;-C2). 4. С помощью функции Подбор параметра определена ставка, при которой выгоднее деньги вложить в инвестиционный проект 8,5%. 1. Внесены исходные ...
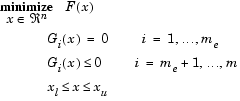
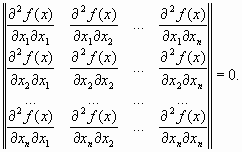
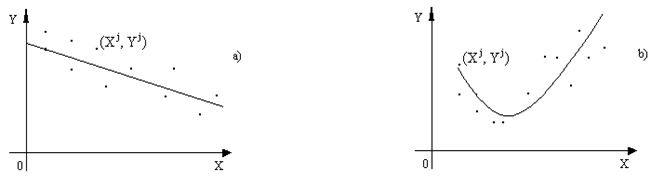
0 комментариев