Навигация
Движение твердого тела в жидкости
30324
знака
7
таблиц
8
изображений
1.2. Движение твердого тела в жидкости
При движении тел в вязкой жидкости возникают силы сопротивления. Происхождение этих сил можно объяснить двумя разными механизмами. При небольших скоростях, когда за телом нет вихрей (ламинарное течение, идеальное обтекание), сила сопротивления обуславливается только вязкостью жидкости. В этом случае прилегающие к телу слои жидкости движутся вместе с телом. Но граничащие с ними слои также увлекаются в движение силами молекулярного сцепления. Так создаются силы, тормозящие относительное движение твердого тела и жидкости. Величину этих силы трения можно рассчитать с использованием формулы Ньютона (1).
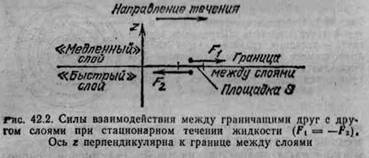
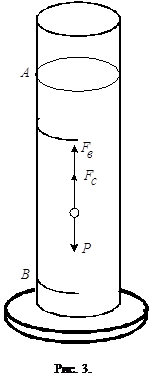Второй механизм возникновения сил сопротивления связан с образованием вихрей и различием скоростей движения жидкости перед телом и за ним (рис.2). Давление в стационарном потоке жидкости меняется в зависимости от скорости потока так, что в области вихрей оно существенно уменьшается (уравнение Бернулли p1+rv12/2=p2+rv22/2). Разность давлений Dp=r(v12 –v22)/2 в областях перед телом и за ним создает силу «лобового» сопротивления (F=DpS) и тормозит движение тела. Часть работы, совершаемой силами трения при движении тела в жидкости, идет на образование вихрей, энергия которых переходит затем в теплоту.
Если движение тела в жидкости происходит медленно, без образования вихрей, то сила сопротивления создается только по первому из описанных механизмов. Для тел сферической формы ее величину определяют по формуле Стокса:
Fc=6phrv (2)
где r- радиус шарика; v - скорость его равномерного движения; h - вязкость жидкости.
2. Определение вязкости жидкости по методу Стокса
2.1. Теория метода
На движущийся шарик в жидкости действуют три силы: сила тяжести - FТ, выталкивающая архимедова сила Fв и сила сопротивления Fc. Силу тяжести и выталкивающую силу можно определить через объем шарика, плотность r шарика и плотность r0 жидкости:
FТ =4pr3rg/3 (3)
Fв=4pr3ro g/3 (4)
Сила тяжести и выталкивающая сила постоянны. Сила сопротивления Fc прямо пропорциональна этой скорости и поэтому на начальном этапе она меньше силы тяжести и шарик падает равноускоренно. При этом сила сопротивления увеличивается и наступает момент, когда все три силы уравновешиваются. Шарик начинает двигаться равномерно:
FТ =Fв + Fc или 4pr3rg/3= 4pr3ro g/3+6phrv, (5)
откуда
(6)
2.2. Экспериментальная установка
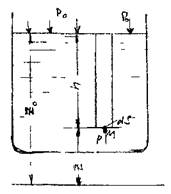
Для определения вязкости жидкости по методу Стокса берется высокий цилиндрический сосуд с исследуемой жидкостью (рис.3). На сосуде имеются две кольцевые метки А и В. Метка А находится несколько ниже уровня жидкости и соответствует той высоте, где силы, действующие на шарик, уравновешивают друг друга и движение становится равномерным. Нижняя метка В нанесена для удобства отсчета времени в момент падения шарика.
Бросая шарик в сосуд, отмечают по секундомеру время t прохождения шариком расстояния l = АВ между двумя метками.
Если в формулу (6) подставить выражение для скорости движения v=l/t и вместо радиуса r ввести диаметр шарика d, то окончательная расчетная формула приобретает вид:
( 7)
2.3.Ход выполнения работы
1. Измеряют расстояние между метками А и В.
2. При необходимости измеряют с помощью ареометра плотность жидкости r0[2].
3. Измеряют микрометром или штангенциркулем диаметр d шарика.
4. Бросив шарик в сосуд с жидкостью, измеряют время t прохождения шариком расстояния между метками А и В.
5. По формуле (7) вычисляют вязкость жидкости h.
6. Аналогичные измерения проделывают с пятью шариками. Результаты измерений и вычислений заносят в таблицу 1 отчета.
7. По результатам всех пяти опытов находят среднее значение вязкости h.
8. Для оценки систематической погрешности измерения вязкости используют расчетную формулу (7). Из нее выводят формулу для вычисления относительной погрешности измерения. При этом считают, что табличные величины, входящие в формулу, не имеют погрешностей, а погрешности измеренных величин l, d, t и r определяются точностью приборов, использованных для их измерения.
9. Полученное значение вязкости сравнивают с табличной величиной для данной жидкости. При объяснении причин расхождения указывают, какой из используемых измерительных приборов вносит в окончательный результат наибольшую погрешность.
Отчет по лабораторной работе №1
«Вязкость жидкостей »
выполненной ……………………………………………. ……….
Определение вязкости жидкости по методу Стокса
Жидкость....................
Расстояние между метками А и В l =…....... ±..... …см
Плотность жидкости r0 = ……± …… г/см3
Плотность материала шарика r = … …± …… г/см3
| № п/п | Диаметр шарика d, мм | Время движения шарика t, с | Вязкость жидкости h, Па× с |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
| 5 |
|
|
|
| Среднее значение вязкости жидкости | |||
Формулы для расчета и расчет погрешности измерения вязкости жидкости1:
Вывод: ……………………………………………………………………………………………..
Дополнительное задание:
Используя полученные значения вязкости, рассчитайте, а затем проверьте экспериментально скорость установившегося движения контрольного тела, выданного вам преподавателем.
Размеры, форма и масса тела:
Материал – Форма -
Диаметр - Масса -
Формула и расчёт скорости движения шарика:
Экспериментальные данные о движении шарика:
Длина пути
Время движения
Скорость движения
Вывод по итогам выполнения задания:
 | |||
| |||
 | |||
Цель работы
Углубить теоретические представления о механизмах возникновения, о величине внутреннего трения в газах, о её связи с микрокинетическими параметрами газа. Освоить методы измерения вязкости газов.
Похожие работы
... состояние равновесия – на поверхность тела действует сила давления жидкости, которая уравновешивает вес жидкости внутри поверхности. Движение жидкостей и газов. Движение жидкостей и газов, как и все другие виды движения, рассматриваемые в механике, можно полностью охарактеризовать, оперируя единицами измерения длины, времени и силы. Так, диаметр парашюта можно измерять в метрах, время ...
... называется кинематической вязкостью. Чтобы отличить ее от v, величину n называют динамической вязкостью. Будучи выраженным через кинематическую вязкость, число Рейнольдса имеет вид 5. Движение тел в жидкостях и газах. Воздействие жидкой или газообразной среды на движущееся в ней с постоянной скоростью v тело будет таким же, каким было бы действие на неподвижное тело набегающего ...
... . Для оценки режима течения жидкости вводят специальный критерий; число кавитации К f ' 7. Истечение жидкости из отверстий и насадков > 7.1. Отверстие в тонкой стенке Одной из типичных задач гидравлики, которую можно назвать задачей прикладного характера, является изучение процессов, связанных с истечением жидкости из отверстия в тонкой стенке и через насадки. ...
... в любых скальных породах не вызывает сомнения. Для понимания процесса формирования полезной емкости коллекторов рассмотрим некоторые факты, полученные за последние годы при изучении различных типов коллекторов нефти и газа. Многими работами последних лет достаточно убедительно показано, что основная полезная емкость коллекторов (терригенных и карбонатных) представляет собой поры, каверны и ...
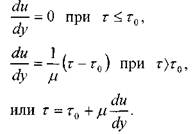
0 комментариев