ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Закон Гесса
Зависимость теплового эффекта реакции от температуры. Закон Кирхгофа
Статистическая интерпретация энтропии
Эндотермические реакции; ΔH > 0
В систему добавлен продукт реакции. В этом случае
ХИМИЧЕСКАЯ КИНЕТИКА
Реакции нулевого порядка
Методы определения порядка реакции
Сложные реакции
Уравнение Аррениуса
Кинетика двусторонних (обратимых) реакций
КАТАЛИТИЧЕСКИЕ ПРОЦЕССЫ
Ферментативный катализ
ОБРАЗОВАНИЕ РАСТВОРОВ. РАСТВОРИМОСТЬ
Взаимная растворимость жидкостей
Температура кристаллизации разбавленных растворов
Понятие активности растворенного вещества
Сильные электролиты
Молярная электропроводность растворов электролитов
Гальванический элемент. ЭДС гальванического элемента
Классификация электродов
Окислительно-восстановительные электроды
Адсорбция на границе раствор – пар
Теории адсорбции
Адсорбция на границе твердое тело – раствор
Методы получения лиофобных коллоидов
Коагуляция лиофобных коллоидов
Двойной электрический слой и электрокинетические явления
Кинетическая устойчивость золей. Седиментация
Навигация
Температура кристаллизации разбавленных растворов
Коллоидная химия
191966
знаков
8
таблиц
41
изображение
3.2.3 Температура кристаллизации разбавленных растворов
Раствор в отличие от чистой жидкости не отвердевает целиком при постоянной температуре; при некоторой температуре, называемой температурой начала кристаллизации, начинают выделяться кристаллы растворителя и по мере кристаллизации температура раствора понижается (поэтому под температурой замерзания раствора всегда понимают именно температуру начала кристаллизации). Замерзание растворов можно охарактеризовать величиной понижения температуры замерзания ΔТзам, равной разности между температурой замерзания чистого растворителя T°зам и температурой начала кристаллизации раствора Tзам:
(III.13)
Рассмотрим Р – T диаграмму состояния растворителя и растворов различной концентрации (рис. 3.5), на которой кривая ОF есть зависимость давления пара над твердым растворителем, а кривые ОА, ВС, DE – зависимости давления пара над чистым растворителем и растворами с возрастающими концентрациями соответственно. Кристаллы растворителя будут находиться в равновесии с раствором только тогда, когда давление насыщенного пара над кристаллами и над раствором одинаково. Поскольку давление пара растворителя над раствором всегда ниже, чем над чистым растворителем, температура, отвечающая этому условию, всегда будет более низкой, чем температура замерзания чистого растворителя. При этом понижение температуры замерзания раствора ΔTзам не зависит от природы растворенного вещества и определяется лишь соотношением числа частиц растворителя и растворенного вещества.
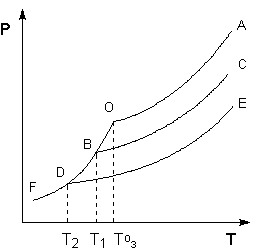
Рис. 3.5 Понижение температуры замерзания разбавленных растворов
Можно показать, что понижение температуры замерзания раствора ΔTзам прямо пропорционально моляльной концентрации раствора:
(III.14)
Уравнение (III.14) называют вторым законом Рауля. Коэффициент пропорциональности K – криоскопическая постоянная растворителя – определяется природой растворителя.
3.2.4 Температура кипения разбавленных растворов
Температура кипения растворов нелетучего вещества всегда выше, чем температура кипения чистого растворителя при том же давлении. Рассмотрим Р – T диаграмму состояния растворителя и растворов различной концентрации (рис.3.5). Любая жидкость – растворитель или раствор – кипит при той температуре, при которой давление насыщенного пара становится равным внешнему давлению. Соответственно температуры, при которых изобара Р = 1 атм. пересечет кривые ОА, ВС и DE, представляющие собой зависимости давления пара над чистым растворителем и растворами с возрастающими концентрациями соответственно, будут температурами кипения этих жидкостей (рис. 3.6).
Повышение температуры кипения растворов нелетучих веществ ΔTк = Tк – T°к пропорционально понижению давления насыщенного пара и, следовательно, прямо пропорционально моляльной концентрации раствора. Коэффициент пропорциональности E есть эбулиоскопическая постоянная растворителя, не зависящая от природы растворенного вещества.
(III.15)
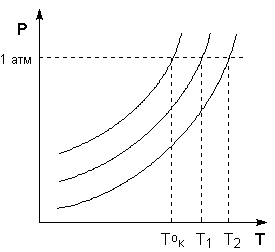
Рис. 3.6 Повышение температуры кипения разбавленных растворов
Т.о., второй закон Рауля можно в наиболее общем виде сформулировать следующим образом:
Понижение температуры замерзания и повышение температуры кипения разбавленного раствора нелетучего вещества прямо пропорционально моляльной концентрации раствора и не зависит от природы растворенного вещества.
Второй закон Рауля является следствием из первого; данный закон справедлив только для бесконечно разбавленных растворов. Коэффициенты пропорциональности в уравнениях (III.14 – III.15) – эбулиоскопическая и криоскопическая константы – имеют физический смысл соответственно повышения температуры кипения и понижения температуры замерзания растворов с моляльной концентрацией, равной 1 моль/кг. Однако, поскольку такие растворы не являются бесконечно разбавленными, эбулиоскопическая и криоскопическая константы не могут быть непосредственно определены и относятся поэтому к числу т.н. экстраполяционных констант.
3.2.5 Осмотическое давление разбавленных растворов
Если разделить два раствора с различной концентрацией полупроницаемой перегородкой, пропускающей молекулы растворителя, но препятствующей переходу частиц растворённого вещества, будет наблюдаться явление самопроизвольного перехода растворителя через мембрану из менее концентрированного раствора в более концентрированный – осмос. Осмотические свойства раствора количественно характеризуются величиной осмотического давления. Давление, которое необходимо приложить к раствору, чтобы предотвратить перемещение растворителя в раствор через мембрану, разделяющую раствор и чистый растворитель, есть осмотическое давление π. Осмотическое давление идеальных растворов линейно зависит от температуры и молярной концентрации раствора С и может быть рассчитано по уравнению (III.16):
(III.16)
Уравнение (III.16) есть т.н. принцип Вант-Гоффа:
осмотическое давление идеального раствора равно тому давлению, которое оказывало бы растворенное вещество, если бы оно, находясь в газообразном состоянии при той же температуре, занимало бы тот же объем, который занимает раствор.
Осмос играет важнейшую роль в процессах жизнедеятельности животных и растений, поскольку клеточная плазматическая мембрана является полупроницаемой. Осмос обусловливает поднятие воды по стеблю растений, рост клетки и многие другие явления.
Рассмотрим роль осмоса в водном режиме растительной клетки. Осмотическое давление жидкости, контактирующей с клеткой, может быть больше, меньше либо равно осмотическому давлению внутриклеточной жидкости. Соответственно выделяют гипертонические, гипотонические и изотонические растворы.
Если клетка находится в контакте с гипертоническим раствором, вода выходит из неё путём осмоса через плазматическую мембрану. Протопласт (живое содержимое клетки) при этом уменьшается в объёме, сморщивается и в конце концов отстаёт от клеточной стенки. Этот процесс называют плазмолизом. Процесс плазмолиза обычно обратим.
Если клетку поместить в чистую воду или гипотонический раствор, вода путём осмоса поступает в клетку; протопласт при этом увеличивается в объёме и оказывает давление на сравнительно жёсткую клеточную стенку. Этот процесс называется тургором. Тургорное давление препятствует дальнейшему поступлению воды в клетку. Именно тургорное давление поддерживает стебли растений в вертикальном положении, придаёт растениям прочность и устойчивость.
Изотонические растворы не оказывают влияния на водный режим клетки.
У животных клеток нет клеточной стенки, поэтому они более чувствительны к осмотическому давлению жидкости, в которой находятся. Животные клетки имеют систему защиты, основанную на осморегуляции; организм животного стремится поддерживать осмотическое давление всех тканевых жидкостей на постоянном уровне. Например, осмотическое давление крови человека – 800 000 Н/м2. Такое же осмотическое давление имеет 0,9 %-ный раствор хлорида натрия. Физиологический раствор, изотоничный крови, широко применяется в медицине.
Похожие работы
... «мицелла» и «мицеллярный раствор». Эти термины были использованы им для обозначения систем, образованных нестехиометрическими соединениями в водной среде. Основная заслуга в становлении коллоидной химии как науки принадлежит Т. Грэму. Как уже отмечалось выше, именно этому ученому принадлежит идея введения термина «коллоид», производного от греческого слова «kolla», обозначающего «клей». Занимаясь ...
... Расстояние, пройденное веществом по сорбенту, прямо пропорционально растворимости данного вещества в пропускаемом растворителе. Даёт возможность полностью разделять вещества, входящие в состав разделяемой смеси. Коллоидная химия Дисперсные системы – это системы, состоящие из множества частиц одной фазы (дисперсной), распределённых в объёме другой фазы – дисперсионной. Дисперсионная среда ...
... и многое другое, без чего немыслима сама жизнь. Все человеческое тело – это мир частиц, находящихся в постоянном движении строго по определенным правилам, подчиняющимся физиологии человека. Коллоидные системы организмов обладают рядом биологических свойств, характеризующих то или иное коллоидное состояние: 2.2 Коллоидная система клеток. С точки зрения коллоидно-химической физиологии ...
... металлов с белками, нуклеиновыми кислотами, липидами. Её практическое применение связано с синтезом фарамакологических препаратов, действие которых обусловленно комплексными ионами металлов. Биоорганическая Химия Изучает связь между строениями органических веществ и их биологическими функциями, использующих в основном методы органической и физической химии, а также физики и математики. ...
0 комментариев