Статистическая интерпретация энтропии

1.4.1 Статистическая интерпретация энтропии

Классическая термодинамика рассматривает происходящие процессы безотносительно к внутреннему строению системы; поэтому в рамках классической термодинамики показать физический смысл энтропии невозможно. Для решения этой проблемы Больцманом в теорию теплоты были введены статистические представления. Каждому состоянию системы приписывается термодинамическая вероятность (определяемая как число микросостояний, составляющих данное макросостояние системы), тем большая, чем более неупорядоченным или неопределенным является это состояние. Т.о., энтропия есть функция состояния, описывающая степень неупорядоченности системы. Количественная связь между энтропией S и термодинамической вероятностью W выражается формулой Больцмана:

(I.58)

С точки зрения статистической термодинамики второе начало термодинамики можно сформулировать следующим образом:

Система стремится самопроизвольно перейти в состояние с максимальной термодинамической вероятностью.

Статистическое толкование второго начала термодинамики придает энтропии конкретный физический смысл меры термодинамической вероятности состояния системы.

1.5 ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ

Ранее мы показали, что внутреннюю энергию системы можно условно представить в виде суммы двух величин "свободной" и "связанной" энергии. Возможность рассчитать величину "свободной" энергии, т.е. той части внутренней энергии системы, которую можно превратить в работу, дает тепловая теорема Нернста, называемая также третьим начало термодинамики.

Основные положения тепловой теоремы заключаются в следующем:

1. При абсолютном нуле температуры свободная энергия X равна теплоте процесса.

(I.59)

2. При температурах, близких к абсолютному нулю, теплоемкость системы равна нулю.

(I.60)

Одной из формулировок третьего начала термодинамики является также постулат Планка:

Энтропия идеального кристалла при абсолютном нуле температуры равна нулю.

Строго говоря, тепловая теорема Нернста и постулат Планка являются следствиями из второго начала термодинамики; но независимо от этого они имеют очень большое значение, позволяя рассчитывать абсолютную энтропию системы и, следовательно, величину свободной энергии системы.

1.5.1 Расчет абсолютной энтропии

Рассчитаем изменение энтропии некоторой системы при нагревании её от абсолютного нуля до температуры T при постоянном давлении. Из первого и второго начал термодинамики имеем:

 (I.61)

 (I.62)

Отсюда:

 (I.63)

Учитывая, что S_T=0 = 0, получим:

(I.64)

При T = 0 любое вещество может находиться только в твердом состоянии. При нагревании вещества возможен его переход в жидкое и затем в газообразное состояние; для фазовых переходов, происходящих в изобарно-изотермических условиях, изменение энтропии равно приведенной теплоте фазового перехода:

(I.65)

Таким образом, нагревание вещества без фазовых переходов сопровождается непрерывным ростом энтропии; при фазовом переходе происходит скачкообразное изменение энтропии. Графическая зависимость энтропии вещества от температуры приведена на рисунке 1.3.

Учитывая это, рассчитать абсолютную энтропию любого вещества при любой температуре можно следующим образом:

(I.66)

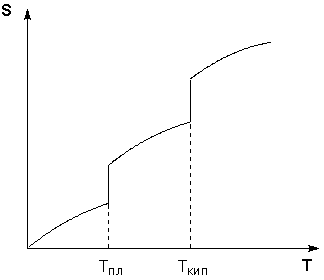
Рис. 1.3 Зависимость энтропии вещества от температуры.

Поскольку энтропия есть функция состояния, изменение энтропии в ходе химического процесса определяется только видом и состоянием исходных веществ и продуктов реакции и не зависит от пути реакции; оно может быть рассчитано по уравнению (I.67):

(I.67)

Для многих веществ величины абсолютной энтропии в стандартных условиях приведены в справочной литературе.

1.6 ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ

Изменение энтропии однозначно определяет направление и предел самопроизвольного протекания процесса лишь для наиболее простых систем – изолированных. На практике же большей частью приходится иметь дело с системами, взаимодействующими с окружающей средой. Для характеристики процессов, протекающих в закрытых системах, были введены новые термодинамические функции состояния: изобарно-изотермический потенциал (свободная энергия Гиббса) и изохорно-изотермический потенциал (свободная энергия Гельмгольца).

Поведение всякой термодинамической системы в общем случае определяется одновременным действием двух факторов – энтальпийного, отражающего стремление системы к минимуму тепловой энергии, и энтропийного, отражающего противоположную тенденцию – стремление системы к максимальной неупорядоченности. Если для изолированных систем (ΔН = 0) направление и предел самопроизвольного протекания процесса однозначно определяется величиной изменения энтропии системы ΔS, а для систем, находящихся при температурах, близких к абсолютному нулю (S = 0 либо S = const) критерием направленности самопроизвольного процесса является изменение энтальпии ΔН, то для закрытых систем при температурах, не равных нулю, необходимо одновременно учитывать оба фактора. Направлением и предел самопроизвольного протекания процесса в любых системах определяет более общий принцип минимума свободной энергии:

Самопроизвольно могут протекать только те процессы, которые приводят к понижению свободной энергии системы; система приходит в состояние равновесия, когда свободная энергия достигает минимального значения.

Для закрытых систем, находящихся в изобарно-изотермических либо изохорно-изотермических условиях свободная энергия принимает вид изобарно-изотермического либо изохорно-изотермического потенциалов (т.н. свободная энергия Гиббса и Гельмгольца соответственно). Данные функции называют иногда просто термодинамическими потенциалами, что не вполне строго, поскольку термодинамическими потенциалами являются также внутренняя энергия (изохорно-изэнтропный) и энтальпия (изобарно-изэнтропный потенциал).

Рассмотрим закрытую систему, в которой осуществляется равновесный процесс при постоянных температуре и объеме. Выразим работу данного процесса, которую обозначим A_max (поскольку работа процесса, проводимого равновесно, максимальна), из уравнений (I.53, I.54):

(I.68)

(I.69)

Преобразуем выражение (I.69), сгруппировав члены с одинаковыми индексами:

(I.70)

Введя обозначение:

(I.71)

получаем:

(I.72)

(I.73)

Функция есть изохорно-изотермический потенциал (свободная энергия Гельмгольца), определяющий направление и предел самопроизвольного протекания процесса в закрытой системе, находящейся в изохорно-изотермических условиях.

Закрытую систему, находящуюся в изобарно-изотермических условиях, характеризует изобарно-изотермический потенциал G:

(I.74)

(I.75)

Поскольку –ΔF = A_max, можно записать:

 (I.76)

Величину А'_max называют максимальной полезной работой (максимальная работа за вычетом работы расширения). Основываясь на принципе минимума свободной энергии, можно сформулировать условия самопроизвольного протекания процесса в закрытых системах.
Условия самопроизвольного протекания процессов в закрытых системах:

Изобарно-изотермические (P = const, T = const):

ΔG < 0, dG < 0

ΔF < 0, dF < 0

Процессы, которые сопровождаются увеличением термодинамических потенциалов, протекают лишь при совершении работы извне над системой. В химии наиболее часто используется изобарно-изотермический потенциал, поскольку большинство химических (и биологических) процессов происходят при постоянном давлении. Для химических процессов величину ΔG можно рассчитать, зная ΔH и ΔS процесса, по уравнению (I.75), либо пользуясь таблицами стандартных термодинамических потенциалов образования веществ ΔG°_обр; в этом случае ΔG° реакции рассчитывается аналогично ΔН° по уравнению (I.77):

(I.77)

Величина стандартного изменения изобарно-изотермического потенциала в ходе химической любой реакции ΔG°₂₉₈ есть мера химического сродства исходных веществ. Основываясь на уравнении (I.75), можно оценить вклад энтальпийного и энтропийного факторов в величину ΔG и сделать некоторые обобщающие заключения о возможности самопроизвольного протекания химических процессов, основываясь на знаке величин ΔН и ΔS.

1. Экзотермические реакции; ΔH < 0.

а) Если ΔS > 0, то ΔG всегда отрицательно; экзотермические реакции, сопровождающиеся увеличением энтропии, всегда протекают самопроизвольно.

б) Если ΔS < 0, реакция будет идти самопроизвольно при ΔН > TΔS (низкие температуры).

Похожие работы

Краткая история развития коллоидной химии как науки

Скачать

14177

0

0

... «мицелла» и «мицеллярный раствор». Эти термины были использованы им для обозначения систем, образованных нестехиометрическими соединениями в водной среде. Основная заслуга в становлении коллоидной химии как науки принадлежит Т. Грэму. Как уже отмечалось выше, именно этому ученому принадлежит идея введения термина «коллоид», производного от греческого слова «kolla», обозначающего «клей». Занимаясь ...

Коллоидная химия и поверхностные явления

Скачать

25685

1

9

... Расстояние, пройденное веществом по сорбенту, прямо пропорционально растворимости данного вещества в пропускаемом растворителе. Даёт возможность полностью разделять вещества, входящие в состав разделяемой смеси. Коллоидная химия Дисперсные системы – это системы, состоящие из множества частиц одной фазы (дисперсной), распределённых в объёме другой фазы – дисперсионной. Дисперсионная среда ...

Коллоидные системы в организме и их функции

Скачать

83726

2

5

... и многое другое, без чего немыслима сама жизнь. Все человеческое тело – это мир частиц, находящихся в постоянном движении строго по определенным правилам, подчиняющимся физиологии человека. Коллоидные системы организмов обладают рядом биологических свойств, характеризующих то или иное коллоидное состояние: 2.2 Коллоидная система клеток. С точки зрения коллоидно-химической физиологии ...

Подразделения химии

Скачать

6800

0

0

... металлов с белками, нуклеиновыми кислотами, липидами. Её практическое применение связано с синтезом фарамакологических препаратов, действие которых обусловленно комплексными ионами металлов. Биоорганическая Химия Изучает связь между строениями органических веществ и их биологическими функциями, использующих в основном методы органической и физической химии, а также физики и математики. ...