Навигация
Кривые и поверхности второго порядка
Кафедра высшей математики
Курсовая работа
По линейной алгебре и аналитической геометрии
«Кривые и поверхности второго порядка»
Дубна 2002
Оглавление
Введение
Часть I. Исследование кривой второго порядка
1. Определение типа кривой с помощью инвариантов
2. Приведение к каноническому виду
3. Построение графиков
4. Вывод
Часть II. Исследование поверхности второго порядка
1. Определение типа поверхности.
2. Приведение к каноническому виду
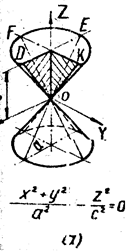
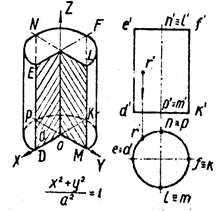
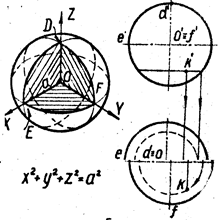
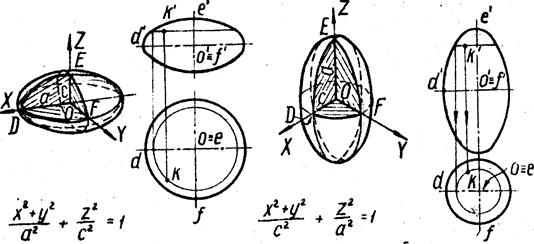
3. Исследование формы поверхности методом сечений
4. Графики уравнения поверхности.
5. Вывод
Введение
Цель:
Целью данной курсовой работы является исследование кривой и поверхности второго порядка. Закрепление теоретических знаний и практических навыков по изучению и анализу свойств кривых и поверхностей второго порядка.
Постановка задачи:
I) Для данного уравнения кривой второго порядка:
1) Определить тип кривой с помощью инвариантов.
2) При a=0 записать каноническое уравнение прямой и определить расположение центра
3) Привести уравнение к каноническому виду, применяя параллельный перенос и поворот координатных осей.
II) Для данного уравнения плоскости второго порядка:
1) Исследовать форму поверхности методом сечений плоскостями, построить линии, полученные в сечениях.
2) Построить поверхность в канонической системе координат.
Часть I. Исследование кривой второго порядка 1. Определение типа кривой с помощью инвариантов
Для данного уравнения кривой второго порядка:
(5 - a)x2 + 4xy + 3y2 + 8x – 6y +5 = 0 (3.1)
определить зависимость типа кривой от параметра a с помощью инвариантов.
Для данного уравнения кривой второго порядка:
a11 = 5 - a, a12 = 2, a13 = 4, a22 = 2, a23 = -3, a33 = 5
Вычислим инварианты:
I1 = a11 + a22 = (5 - a) +2 = 7 - a
I2 =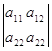 =
=![]() = (5 - a)2 – 4 = 6 -2a
= (5 - a)2 – 4 = 6 -2a
I2 =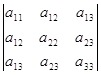 =
=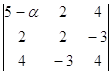 = (5 - a)10-24-24-32-9(5 - a)-20 = -a-95
= (5 - a)10-24-24-32-9(5 - a)-20 = -a-95
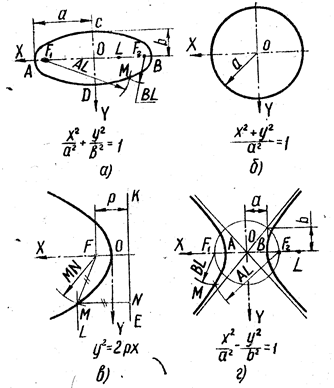
Согласно классификации кривых второго порядка:
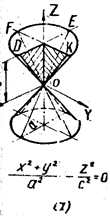
I. Если I2 = 0, то данное уравнение (3.1) определяет кривую параболического типа:
I2 = 6 - 2a = 0, следовательно, при a = 3 уравнение определяет кривую параболического типа.
При a = 3 I3 = - a - 95 = -3 - 95 = 98 ¹ 0. Значит, при a = 3 уравнение (3.1) задаёт параболу.
II. Если I2 ¹ 0, то задаваемая кривая является центральной. Следовательно, при a ¹ 3 данное уравнение задаёт центральную кривую.
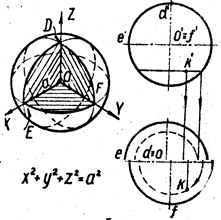
1. Если I2 > 0, то уравнение задаёт кривую эллиптического типа:
Значит, при a < 3 уравнение (3.1) задаёт кривую эллиптического типа.
a. Если I1 I3 < 0, то уравнение определяет эллипс:
I1 I3 = - (7 - a)(a+95) = a2+88a-665 < 0, при решении получаем a Î (-95 , 7). Следовательно, при a Î (-95 , 3) уравнение (3.1) задаёт эллипс.
b. Если I1 I3 > 0, то уравнение определяет эллипс:
I1 I3 = a2+88a-665 > 0, при решении получаем a Î (-¥, -95). Следовательно, при a Î (-¥ , -95) уравнение (3.1) задаёт мнимый эллипс.
c. Если I3 = 0, то уравнение определяет две мнимые пересекающиеся прямые:
I3 = -a - 95 = 0, при решении получаем a - 95. Следовательно, при a = - 95 уравнение (3.1) задаёт две мнимые пересекающиеся прямые.
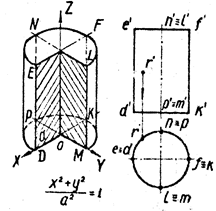
2. Если I2 < 0, то уравнение задаёт кривую гиперболического типа:
Значит, при a > 3 уравнение (3.1) задаёт кривую гиперболического типа.
a. Если I3 ¹ 0, то уравнение определяет гиперболу:
I3 = -a - 95 ¹ 0, получаем a ¹ -95. Следовательно, при a Î (3 , +¥) уравнение (3.1) задаёт гиперболу.
Согласно полученным данным, построим таблицу:
| a Î (-¥ , -95) | a = -95 | a Î (-95 , 3) | a = 3 | a Î (3 , +¥) |
| Мнимый эллипс | Две мнимые пересекающиеся прямые | Эллипс | Парабола | Гипербола |
При a = 0 уравнение (3.1) принимает вид:
5x2 + 4xy + 2y2 + 8x - 6y + 5 = 0 (3.2)
Приведем уравнение кривой (3.2) к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. Мы установили, что данная кривая — центральная, поэтому используем методику приведения к каноническому виду для уравнения центральной кривой.
a) Характеристическое уравнения для данной кривой будет иметь вид:
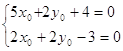
A(x, y) = 5x2 + 4xy + 2y2
![]()
Откуда следует, корни характеристического уравнения есть: l1 = 1, l2 = 6.
Расположение эллипса относительно начальной системы координат будет известно, если мы будем знать координаты центра и угловой коэффициент вещественной оси эллипса.
Уравнения для определения координат центра имеют вид:
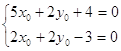
Откуда мы находим x0 = - ![]() и y0 =
и y0 = ![]() . Следовательно, точка O¢ (-
. Следовательно, точка O¢ (-![]() ,
,![]() ) есть центр данной кривой.
) есть центр данной кривой.
Угловой коэффициент оси O¢X можем определить по формуле:
![]()
б) Совершим параллельный перенос начала координат в точку O¢ (x0, y0). При этом координаты x, y произвольной точки плоскости в системе координат xOy и координаты x', y' в новой системе координат x'O'y' связаны соотношениями:
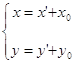
Подставив данные выражения в уравнение (3.1), получим:
5(x0 + x¢)2 + 4(x0 + x¢)(y0 + y¢) + 2(y0 + y¢)2 + 8(x0 + x¢) - 6(y0 + y¢) + 5=0
Раскрыв скобки и приведя подобные члены, получим:
5x¢2+4x¢y¢+2y¢2+(10x0+4x0 + 8)x¢ + (4x0 + 4y0 - 6)y¢ + (5x02 + 4x0y0 + 2y02 + 8x0 - 6y0 + 5) = 0 (3.3)
В данном уравнении коэффициенты при x¢ и y¢ приравняем к нулю и получим систему уравнений:
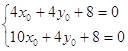
Решив эту систему уравнений, мы получим, найденные уже раннее, координаты центра O¢ , x0 = - ![]() и y0 =
и y0 = ![]() . Подставив данные значения в уравнение (3.3), коэффициенты при x¢ и y¢ станут равными нулю, мы получим уравнение в системе координат x'O'y' :
. Подставив данные значения в уравнение (3.3), коэффициенты при x¢ и y¢ станут равными нулю, мы получим уравнение в системе координат x'O'y' :
5x¢2 + 4x¢y¢ + 2y¢2 + (![]() ) = 0
) = 0
5x¢2 + 4x¢y¢ + 2y¢2 - ![]() = 0 (3.4)
= 0 (3.4)
в) Так как a12 = 2 ¹ 0, то для дальнейшего упрощения необходимо произвести поворота осей координат на угол a. При повороте осей координат на угол a координаты x', y' произвольной точки М плоскости в системе координат x'O'y' и координаты X, Y в новой системе координат XO'Y связаны соотношениями:
![]()
Подставим данные выражения в уравнение (3.4), получим:
5(Xcosa - Ysina)2 + 4(Xcosa - Ysina)(Xsina + Ycosa) + 2(Xsina + Ycosa)2 - ![]() = 0
= 0
(5cos2a + 4sinacosa + 2sin2a)X2 + (-6sinacosa + 4cos2a - 4sin2a)XY +
(5sin2a - 4sinacosa + 2cos2a)Y2 - ![]() = 0 (3.5)
= 0 (3.5)
В полученном выражении найдём такой угол a, чтобы коэффициент при XY стал равен нулю, для этого необходимо:
-6sinacosa + 4cos2a - 4sin2a = 0
2tg2a + 3tga - 2=0
Откуда, при решении, находим два значения tga = -2 и tga = ![]() .
.
В первом задании мы нашли, что угловой коэффициент вещественной оси O'X эллипса равен k = -2. Так как угловой коэффициент равен тангенсу, то из двух найдённых значений выберем tga = -2. Следовательно:
cosa = ![]() , sina =
, sina = ![]()
Подставив данные значения для sina и cosa в уравнение (3.5), коэффициент при XY станет равным нулю, получим:
(![]() )X2 + (
)X2 + (![]() )Y2 -
)Y2 - ![]() = 0
= 0
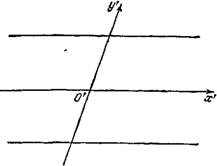
X2 + 6Y2 - ![]() = 0
= 0
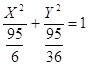 (3.6)
(3.6)
- это каноническое уравнение данной кривой (3.1) при a = 0.
3. Построение графиковПодтвердим результаты проведённого исследования данного уравнения кривой (3.1) второго порядка, построив соответствующие графики кривых при разных a.
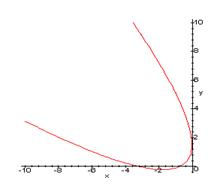
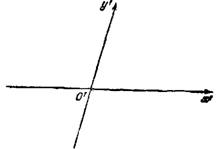
При a = 3 уравнение (3.1) принимает вид:
2x2 + 4xy + 3y2 + 8x – 6y +5 = 0
Графиком данного уравнения является парабола:
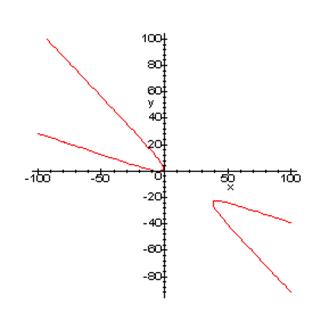
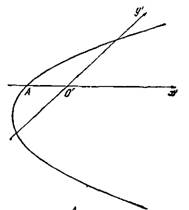
При a = 6 уравнение (3.1) принимает вид:
x2 + 4xy + 3y2 + 8y2 – 6y +5 = 0
Графиком данного уравнения является гипербола:
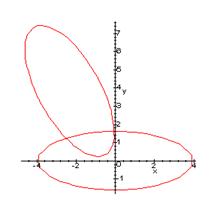
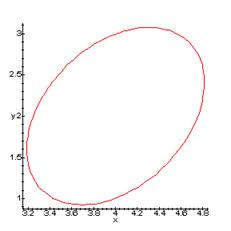
При a = 0 уравнение (3.1) принимает вид
5x2 + 4xy + 3y2 + 8y2 – 6y +5 = 0
Графиком данного уравнения является эллипс. Изобразим в данной системе также график канонического уравнения эллипса (3.6):
Похожие работы
... кривой второго порядка и приведя его к каноническому виду, мы установили, что данная кривая — эллипс. Мы получили каноническое уравнение гиперболы при помощи преобразований параллельного переноса и поворота координатных осей. Исследование формы поверхности второго порядка Теоретическая часть Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные ...
... линию называют образующей. Она может быть прямой, тогда образованную ей поверхность относят к классу линейчатых. Если образующая – кривая линия, поверхность считают нелинейчатой. Линию, по которой перемещают образующую, называют направляющей. В качестве последней иногда используют след поверхности. Определителем поверхности называют совокупность условий, задающих поверхность в пространстве. ...
... поверхности, которые в пересечении с данными поверхностями дают простые для построения линии (например, прямые или окружности). В общем случае вспомогательные секущие плоскости применяют и для построения линии пересечения кривой поверхности гранной. Изложенный общий способ построения линии пересечения одной поверхности другою не исключает применения другого способа, если хотя бы одна из этих ...
... в том, что оно легко может быть перенесено на случай поверхностей F{x, у, z) = 0 (и даже на случай (n-1) -мерных поверхностей второго порядка в n-мерном пространстве). Обозначим через C множество точек, лежащих на кривой F(x, у) = а11х2 + 2а12ху + а22у2 + 2а1х + 2а2у + а0 = 0 (6) т. е. множество всех точек М=(х,у) комплексной плоскости, удовлетворяющих уравнению (6). Предположим, что ...
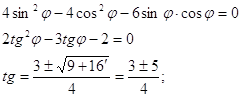
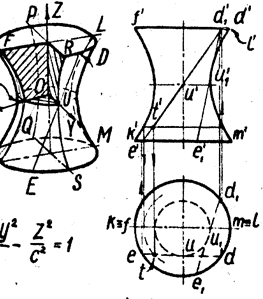

0 комментариев