Навигация
4. Вывод
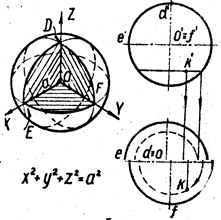
Исследовав данное общее уравнение кривой второго порядка, мы установили, что при значении параметра a = 0 уравнение задаёт эллипс. Привели уравнение к каноническому виду, применяя преобразования параллельного переноса и поворота. При параллельном переносе коэффициенты при первых степенях стали равны нулю, при повороте координатных осей коэффициенты при смешанном произведении стали равны нулю. Построили графики для всех фигур, которое может задавать данное уравнение, построили график эллипса в общей и канонической системе координат.
Часть II. Исследование поверхности второго порядка 1. Определение типа поверхности
Для данного уравнения поверхности второго порядка:
4x2 - z2 + 12xz + 6y - 8z + 5 = 0 (4.1)
Определить тип поверхности с помощью инвариантов.
![]() 4 + 0 -1 = 3
4 + 0 -1 = 3
 = - 4 – 36 = - 40
= - 4 – 36 = - 40
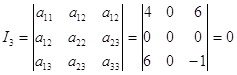
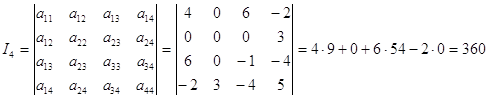
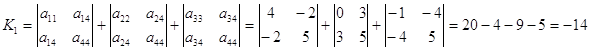
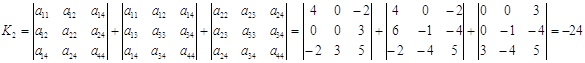
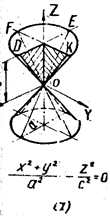
Определим характер расположения центра: Данная поверхность не имеет центра, так как выполняется условие I3 = 0, I4 ¹ 0. При этом инвариант I4 = 360 > 0, следовательно, графиком уравнения (4.1) является гиперболический параболоид.
2. Приведение к каноническому виду
Совершим параллельный перенос начала координат в некоторую точку O'(x0 ,y0, z0). При этом координаты x, y, z произвольной точки пространства в системе координат Oxyz и координаты x', y', z' этой же точки в новой системе координат в системе координат O'x'y'z' связаны соотношением:
 (4.2)
(4.2)
Подставляя уравнения (4.2) в уравнение (4.1) получим уравнение поверхности S в новой системе координат O'x'y'z' :
4(x'+x0)2 - (z'+z0)2 + 12(x'+x0)(z'+z0) + 6y' - 8(z'+z0) + 5 = 0
4x'2 + 8x'x0 + 4x02 - z'2 - 2z'z0 - z02 + 12x'z' + 12z'z0 + 12x0z' + 12x0z0 + 6y' - 8z' - 8z0 + 5 = 0
4x'2 - z'2 + 12x'z' + 6y' + (12x0 - 2z0 - 8)z' + (8x0 + 12z0)x' + (4x02 - z02 + 12x0z0 - 8z0 +5)=0 (4.3)
Для того, чтобы новое начало координат O'(x0, y0, z0) было центром поверхности (4.1) необходимо и достаточно, чтобы в уравнении (4.3) отсутствовал член с x' и z' в первой степени:
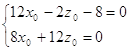
Решая данную систему, находим x0 = ![]() и y0 =
и y0 = ![]() . Подставим полученные значения в уравнение (4.2):
. Подставим полученные значения в уравнение (4.2):
4x'2 - z'2 + 12x'z' + 6y' + (![]() )z' + (
)z' + (![]() )x' + (
)x' + (![]() ) = 0
) = 0
4x'2 - z'2 + 12x'z' + 6y' + ![]() =0 (4.4)
=0 (4.4)
Поскольку коэффициент при x'z' не равен нулю, то продолжим дальнейшее преобразование, совершив поворот осей координат на угол a. Координаты произвольной точки поверхности будут связаны следующими соотношениями:
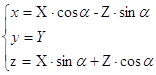 (4.5)
(4.5)
Подставив выражения из (4.5) в уравнение (4.4), получим следующее:
4(Xcosa - Zsina)2 – (Xsina + Zcosa)2 + 12(Xcosa - Zsina)(Xsina + Zcosa) + 6Y + ![]() = 0
= 0
4X2cos2a - 8XZcosasina + 4Z2sin2a - X2sin2a - 2XZsin2a - 2XZcosasina -Z2cos2a + 12X2cosasina + 12XZcos2a - 12XZsin2a - 12Z2sinacosa + 6Y + ![]() = 0
= 0
(4cos2a-sin2a+12cosasina)X2+(4sin2a-cos2a-12sinacosa)+(-8cosasina-2cosasina+12cos2a-12sin2a)XZ+6Y+![]() =0 (4.6)
=0 (4.6)
Найдём угол a такой, что коэффициент при XZ будет равен нулю:
-8cosasina-2cosasina+12cos2a-12sin2a=0
6tg2a+5tga-6=0
D = 25+144 = 169 = 132
Откуда следует, что tga = ![]() или tga =
или tga = ![]() . Возьмём tga =
. Возьмём tga = ![]() . Тогда найдём cosa=
. Тогда найдём cosa= =
=![]() , sina=
, sina=![]() . Подставим найдённые значения в уравнение (4.6):
. Подставим найдённые значения в уравнение (4.6):
(![]() )X2+(
)X2+(![]() )Z2+(
)Z2+(![]() )XZ+6Y+
)XZ+6Y+![]() =0
=0
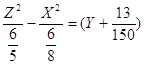 (4.7)
(4.7)
- это каноническое уравнение поверхности (4.1). Оно имеет сдвиг по оси O'Y на (-![]() ).
).
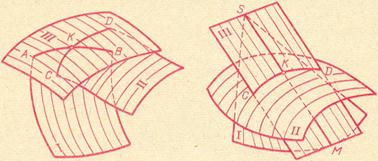
Проведём исследование графика уравнения (4.7) методом сечения плоскостями.
Рассмотрим линии ![]() , полученные в сечениях гиперболического параболоида плоскостями Y=h. Эти линии определяются системой уравнений:
, полученные в сечениях гиперболического параболоида плоскостями Y=h. Эти линии определяются системой уравнений:
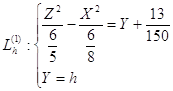
Следовательно, уравнения проекций линий ![]() на плоскость ZO'X имеют вид:
на плоскость ZO'X имеют вид:
![]() :
:
Рассмотрим три случая:
Если h + ![]() >0, h >
>0, h >![]() , запишем полученное уравнение в виде:
, запишем полученное уравнение в виде:
 (4.8)
(4.8)
Уравнение (4.8) задаёт гиперболы с центрами в точках (0, h ,0).
Полуоси гипербол:
a =  - действительная полуось, b =
- действительная полуось, b =  - мнимая полуось, увеличиваются с увеличением h. При различных значениях h получим семейство соответствующих гипербол:
- мнимая полуось, увеличиваются с увеличением h. При различных значениях h получим семейство соответствующих гипербол:
h = 1 a=![]() ; b=
; b=![]() ;
; 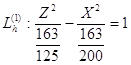
h=2 a=![]() ; b=
; b=![]() ;
; 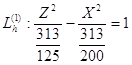
h=3 a=![]() ; b=
; b=![]() ;
; 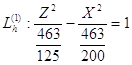
Изобразим данные гиперболы на рисунке:
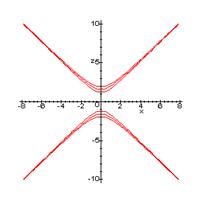
Если h + ![]() =0, h =
=0, h =![]() , запишем полученное уравнение в виде:
, запишем полученное уравнение в виде:
 или
или ![]()
Данное уравнение задаёт две пересекающиеся прямые. Изобразим их на рисунке:

Если h + ![]() < 0, h<
< 0, h<![]() , запишем полученное уравнение в виде:
, запишем полученное уравнение в виде:
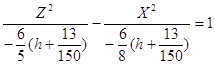
Данное уравнение задаёт сопряжённые гиперболы с центрами в точке (0, h, 0).
Полуоси гипербол:
a=![]() - действительная полуось, b=
- действительная полуось, b=![]() - мнимая полуось, увеличиваются с увеличением | h |.
- мнимая полуось, увеличиваются с увеличением | h |.
При различных значениях h получаем семейство соответствующих гипербол:
h=-1 a=![]() ; b=
; b=![]() ;
; 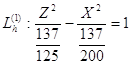
h=-2 a=![]() ; b=
; b=![]() ;
; 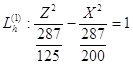
h=-3 a=![]() ; b=
; b=![]() ;
; 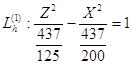
Изобразим данные гиперболы на рисунке:
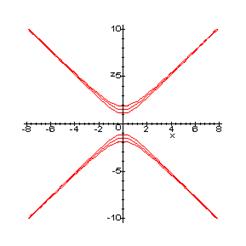
Рассмотрим линии ![]() , полученные в сечениях гиперболического параболоида плоскостями Z=h. Эти линии определяются системой уравнений:
, полученные в сечениях гиперболического параболоида плоскостями Z=h. Эти линии определяются системой уравнений:
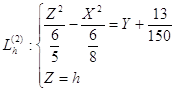
Следовательно, уравнения проекций линий ![]() на плоскость XO'Y имеют вид:
на плоскость XO'Y имеют вид:
![]() :
:![]() (4.9)
(4.9)
Уравнение (4.9) задаёт параболы, с вершинами в точках V(0, ![]() , h) и параметром
, h) и параметром
p=![]() . При различных h получим семейство соответствующих парабол:
. При различных h получим семейство соответствующих парабол:
h = ±1 ![]() :
:![]()
h = ±2 ![]() :
:![]()
h = ±3 ![]() :
:![]()
Изобразим данные параболы на рисунке:
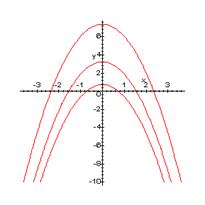
Рассмотрим линии ![]() , полученные в сечениях гиперболического параболоида плоскостями X=h. Эти линии определяются системой уравнений:
, полученные в сечениях гиперболического параболоида плоскостями X=h. Эти линии определяются системой уравнений:
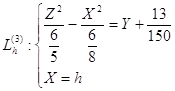
Следовательно, уравнения проекций линий ![]() на плоскость YO'Z имеют вид:
на плоскость YO'Z имеют вид:
![]() (4.10)
(4.10)
Уравнение (4.10) задаёт параболы, с вершинами в V(h, ![]() ,0) и параметром p=
,0) и параметром p=![]() . При различных h получаем семейство соответствующих парабол.
. При различных h получаем семейство соответствующих парабол.
h = ±1 ![]() :
:![]()
h = ±2 ![]() :
:![]()
h = ±3 ![]() :
:![]()
Изобразим данные параболы на рисунке:

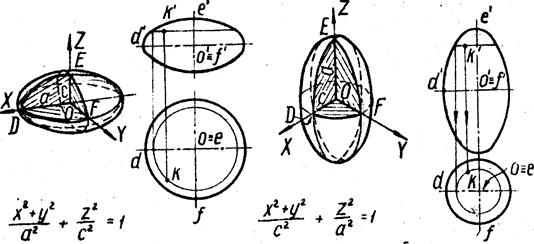
4. Графики уравнения поверхности
Изобразим поверхность второго порядка в общеалгебраической и канонической системе координат.
График в общеалгебраической системе координат:

График в канонической системе координат:
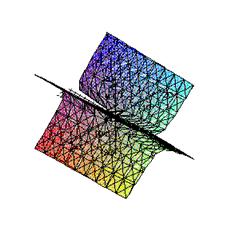
Исследовав каноническое уравнение (4.7) гиперболического параболоида, отметим следующее:
1. Оси O'Z и O'X являются осями симметрии поверхности. Центра симметрии у поверхности нет.
2. Рассекая поверхность горизонтальными плоскостями Y = h, в сечениях получаем:
h > ![]() - гиперболы с действительными осями, параллельными оси O'Z
- гиперболы с действительными осями, параллельными оси O'Z
h = ![]() - две пересекающиеся прямые
- две пересекающиеся прямые
h < ![]() - сопряжённые гиперболы с действительными осями, параллельными оси O'Y
- сопряжённые гиперболы с действительными осями, параллельными оси O'Y
3. Рассекая поверхность плоскостями Z = h и X = h, в сечениях получаем параболы, с ветвями, направленными вниз (Z = h) или вверх (X = h).
4. Поверхность гиперболического параболоида бесконечна в направлении всех трёх координатных осей.
Список литературы
1. Копылова Т. В. Аналитическая геометрия. — Дубна: Международный университет природы, общества и человека «Дубна», 1997.
2. Ильин В. А., Позняк Г. Д. Аналитическая геометрия. — М.: Наука, 1974.
Похожие работы
... кривой второго порядка и приведя его к каноническому виду, мы установили, что данная кривая — эллипс. Мы получили каноническое уравнение гиперболы при помощи преобразований параллельного переноса и поворота координатных осей. Исследование формы поверхности второго порядка Теоретическая часть Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные ...
... линию называют образующей. Она может быть прямой, тогда образованную ей поверхность относят к классу линейчатых. Если образующая – кривая линия, поверхность считают нелинейчатой. Линию, по которой перемещают образующую, называют направляющей. В качестве последней иногда используют след поверхности. Определителем поверхности называют совокупность условий, задающих поверхность в пространстве. ...
... поверхности, которые в пересечении с данными поверхностями дают простые для построения линии (например, прямые или окружности). В общем случае вспомогательные секущие плоскости применяют и для построения линии пересечения кривой поверхности гранной. Изложенный общий способ построения линии пересечения одной поверхности другою не исключает применения другого способа, если хотя бы одна из этих ...
... в том, что оно легко может быть перенесено на случай поверхностей F{x, у, z) = 0 (и даже на случай (n-1) -мерных поверхностей второго порядка в n-мерном пространстве). Обозначим через C множество точек, лежащих на кривой F(x, у) = а11х2 + 2а12ху + а22у2 + 2а1х + 2а2у + а0 = 0 (6) т. е. множество всех точек М=(х,у) комплексной плоскости, удовлетворяющих уравнению (6). Предположим, что ...
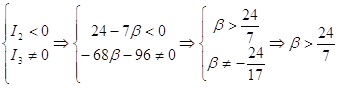
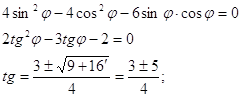

0 комментариев