Навигация
Канашский филиал
КОНТРОЛЬНАЯ РАБОТА № 1
По математике
Вариант 3
Студента 1 курса экономического факультета
Шифр: 04653033 Учебная группа: 53-06
Работа выслана в Чувашский госуниверситет
«____» ____________2006 г.
Передана на кафедру «Экономики и управления»
Оценка___________ «___» _____________2006г.
Преподаватель: Бычков Владимир Порфирьевич
Возвращена в деканат______________________
Математика
Вариант 3
Даны вершины А(х1;у1) ,В(х2;у2), С(х3;у3) треугольника. Требуется найти: 1)длину стороны ВС; 2)площадь треугольника; 3)уравнение стороны ВС; 4)уравнение высоты проведенной из вершины А; 5)длину высоты проведенной из вершины А; 6)уравнение биссектрисы внутреннего угла![]() ;
;
7)угол ![]() в радианах с точностью до 0,01; 8)систему неравенств определяющих множество точек треугольника. Сделать чертеж.
в радианах с точностью до 0,01; 8)систему неравенств определяющих множество точек треугольника. Сделать чертеж.
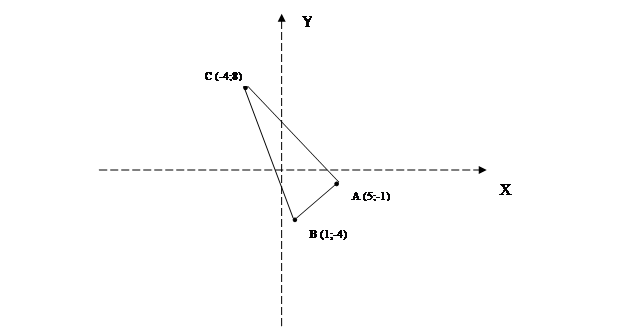
вариант 3: А(5;-1), В(1;-4), С(-4;8).
Решение:
1)Длина стороны ВС:
![]()
![]() ;
;
2)Длина стороны АВ:
![]() ;
;
Скалярное произведение векторов ![]() и
и![]()
![]()
Угол ![]() :
:
![]() cos
cos ![]() =
=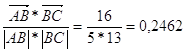 ;
; ![]() =arcos 0,2462=75,75
=arcos 0,2462=75,75![]() ;
;
3) Уравнение стороны ВС:
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
4) Уравнение высоты, проведенной из вершины А:
![]() ;
; ![]() ;
;
Условие перпендикулярности двух прямых:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
5) Длина высоты, проведенной из вершины А:
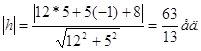
6) ![]()
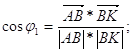
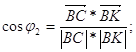
![]()
![]()
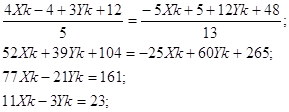
Уравнение прямой АС:
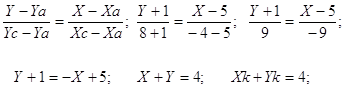
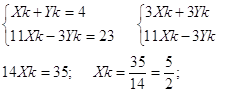
![]()
![]()
Уравнение биссектрисы внутреннего угла ![]() :
:
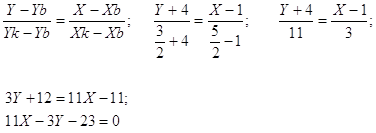
7) Угол ![]() в радианах с точностью до 0,01:
в радианах с точностью до 0,01:
![]()
8) Уравнение стороны ВС:
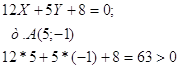
Уравнение стороны АС:
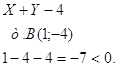
Уравнение стороны АВ:
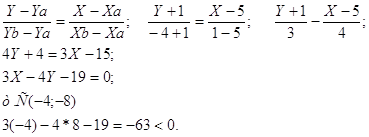
Система неравенств, определяющих множество внутренних точек треугольника.
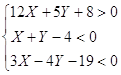
![]() Задание 13.
Задание 13.
Составить уравнение прямой, проходящей через точку А(4;1) на расстоянии 4 единиц от точки В(-4;0).
Решение:
Уравнение пучка прямых, проходящих через точку А:
![]()
По условию задачи ![]()
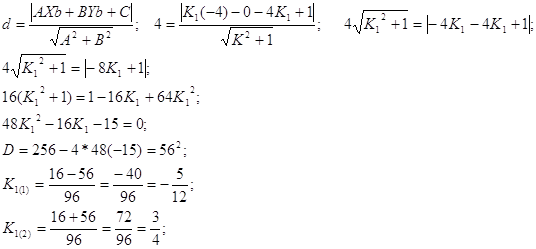
Искомые прямые:
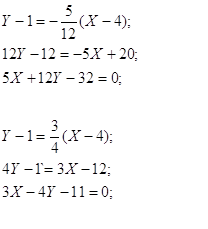
Задание 23.
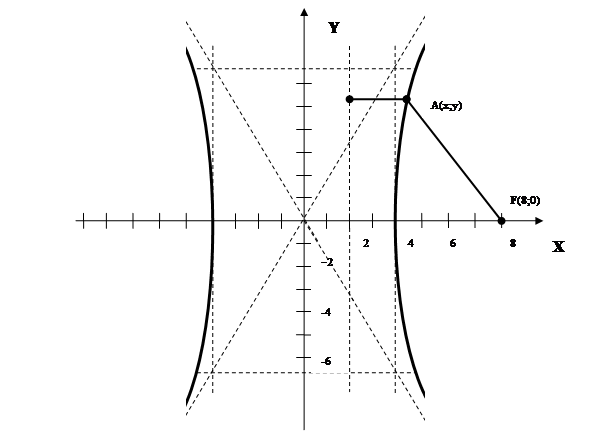
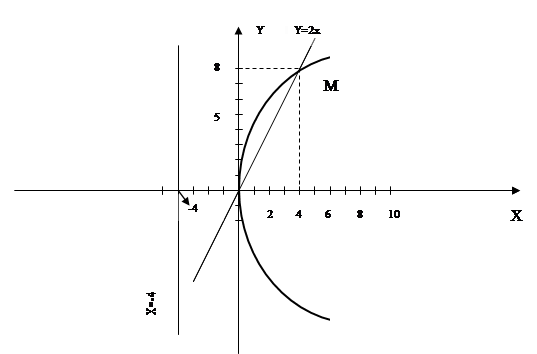
Составить уравнение линии, расстояние каждой точки которой от точки F(8;0) вдвое больше, чем от прямой Х-2=0. Сделать чертеж.
Решение:
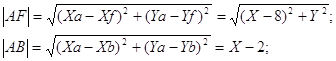
По условию задачи: ![]()
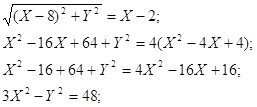
![]() - уравнение гиперболы с центром в точке
- уравнение гиперболы с центром в точке ![]() и полуосями
и полуосями ![]()
![]()
Задание 33.
Составить уравнение параболы и ее директрисы, если известно что парабола проходит через точки пересечения прямой
![]() с окружностью
с окружностью ![]() и ось
и ось ![]() является осью симметрии параболы. Сделать чертеж.
является осью симметрии параболы. Сделать чертеж.
Решение.
Рассмотрим уравнение окружности:
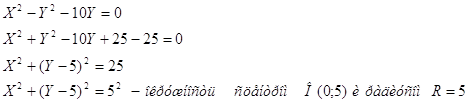
Найдем точки пересечения окружности и прямой.
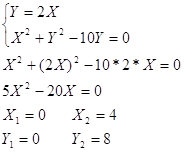
Координаты точек пересечения окружности и прямой ![]() т.к. парабола симметрична относительно ОХ, то уравнение имеет вид
т.к. парабола симметрична относительно ОХ, то уравнение имеет вид ![]() учитывая что
учитывая что ![]() найдем параметр p
найдем параметр p
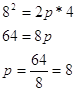
Таким образом, уравнение параболы ![]()
Уравнение директрисы параболы: ![]()
Задание 43.
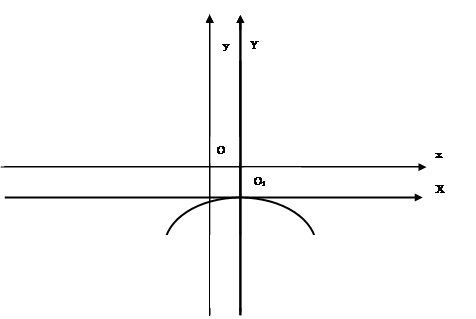
Дано уравнение параболы f(x;y)=0. Сделать параллельный перенос осей координат так, чтобы в новой системе координат XO1Y уравнение параболы приняло вид X2=aY или Y2=aX. Построить обе системы координат и параболу.
![]()
Решение:
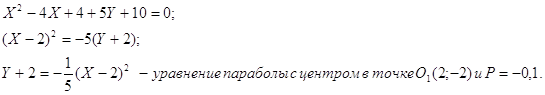
Задание 53
Даны вершины А1(Х1;Y1;Z1),. А2(Х2;Y2;Z2), А3(Х3;Y3;Z3), А4(Х4;Y4;Z4)
пирамиды. Требуется найти: 1) длину ребра А1А2; 2)Угол между ребрами А1А2 и А1А4; 3)угол между ребром А1А2 и гранью А1А2 А3; 4) площадь грани А1А2 А3; 5) объем пирамиды; 6) уравнение высоты, опущенной из вершины А4 на грань А1А2 А3; 7) уравнение плоскости, проходящей через высоту пирамиды, опущенной из вершины А4 на грань А1А2 А3, и вершину А1 пирамиды.
A1(3;5;4), А2(5;8;3), А3(1;9;9), A4(6;4;8);
Решение:
1) ![]()
![]()
![]()
Длина ребра А1А2;
![]()
2) ![]()
![]()
![]()
Длина ребра А1А4;
![]()
Скалярное произведение векторов А1А2 и А1А4:
![]()
![]()
![]()
![]()
Угол между ребрами А1А2 и А1А4:
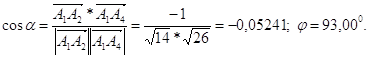
3) Уравнение грани А1А2 А3:
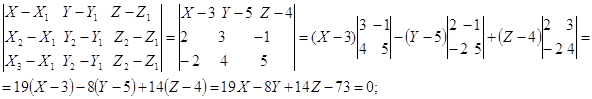
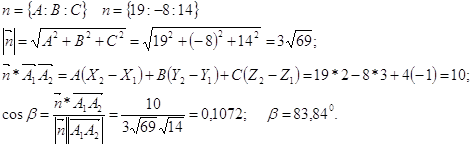
Угол между ребром А1А2 и гранью А1А2 А3:
![]()
4)Площадь грани А1А2А3:
![]() кв. ед.
кв. ед.
5) Объем пирамиды:
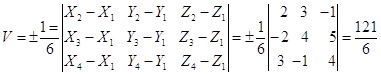 куб. ед.
куб. ед.
6) уравнение высоты, опущенной из вершины А4 на грань А1А2 А3:
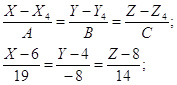
7) Уравнение плоскости, проходящей через высоту пирамиды, опущенной из вершины А4 на грань А1А2 А3, и вершину А1 пирамиды.
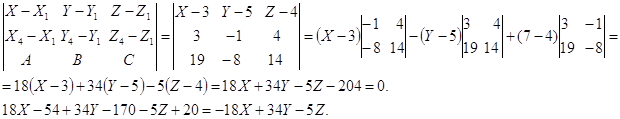
Задание 63.
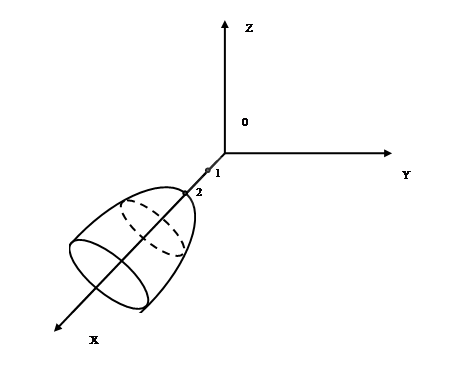
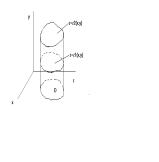
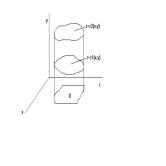
Определить вид поверхности, заданной уравнением f(x;y;z)=0, и показать её расположение относительно системы координат.
![]()
Решение:
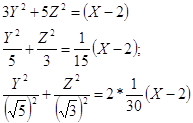
Эллиптический параболоид с вершиной О(z;o;o), направленный вдоль оси ОХ, и имеющий полуоси на оси ![]() по оси
по оси ![]()
Задание 73.
Применяя метод исключения неизвестных, решить систему уравнений.
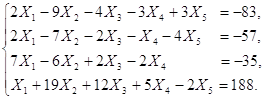
Решение:
| 2 | -9 | -4 | -3 | 3 | -83 | = > = > | 0 | -47 | -28 | -13 | 7 | -459 | ||
| 2 | -7 | -2 | -1 | -4 | -57 | 0 | -45 | -26 | -11 | 0 | -433 | |||
| 7 | -6 | 2 | -2 | 0 | -35 | 0 | -139 | -82 | -37 | -14 | -1351 | |||
| 1 | 19 | 12 | 5 | -2 | 188 | 1 | 19 | 12 | 5 | -2 | 188 | |||
| 0 | -47/7 | -4 | -13/7 | 1 | -459/7 | 0 | 68/77 | 30/77 | 0 | 1 | 980/77 | |||
| 0 | -45 | -26 | -11 | 0 | -433 | 0 | 45/11 | 26/11 | 1 | 0 | 433/11 | |||
| 0 | -233 | -138 | -63 | 0 | -2269 | 0 | 272/11 | 120/11 | 0 | 0 | 2320/11 | |||
| 1 | 39/7 | 4 | 3/7 | 0 | 398/7 | 1 | 94/77 | -190/77 | 0 | 0 | 481/77 | |||
| ||||||||||||||
| 0 | 0 | 0 | 0 | 1 | -2900/77 |
| ||||||||
| 0 | -19/15 | 0 | 1 | 0 | -2583/11 |
| ||||||||
| 0 | 13,6 | 1 | 0 | 0 | 116 |
| ||||||||
| 1 | 1574/231 | 0 | 0 | 0 | 22521/77 |
| ||||||||
Общее решение системы:
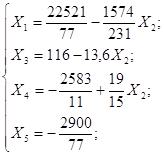
Задание 83.
Даны векторы ![]() и
и ![]() . Показать, что векторы
. Показать, что векторы ![]() образуют базис четырехмерного пространства, и найти координаты вектора
образуют базис четырехмерного пространства, и найти координаты вектора ![]() в этом базисе.
в этом базисе.
![]()
Решение:
Составим определитель из координат векторов ![]() и вычислим его:
и вычислим его:
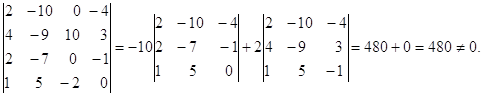
Так как ![]() ,то векторы
,то векторы ![]() составляют базис. Найдем координаты вектора
составляют базис. Найдем координаты вектора ![]() в этом базисе:
в этом базисе:
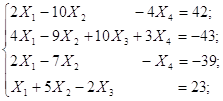
| 2 | -10 | 0 | -4 | -42 | = > | 0 | -20 | 4 | -4 | -88 | = > | 0 | 48 | -12 | 252 | ||||
| 4 | -9 | 10 | 3 | -43 | 0 | -29 | 18 | 3 | -135 | 0 | -80 | 30 | -350 | ||||||
| 2 | -7 | 0 | -1 | -39 | 0 | -17 | 4 | -1 | -85 | 0 | 17 | -4 | 85 | ||||||
| 1 | 5 | -2 | 0 | 23 | 1 | 5 | -2 | 0 | 23 | 1 | 5 | -2 | 23 |
| 0 | -4 | 1 | 0 | -21 | = > | 0 | 0 | 1 | 0 | 3 | ||
| 0 | 40 | 0 | 0 | 240 | 0 | 1 | 0 | 0 | 6 | |||
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | -5 | |||
| 1 | -3 | 0 | 0 | -19 | 1 | 0 | 0 | 0 | -1 |
Итак ![]()
Проверка:
2(-1)-10*6 -4(-5)=-42; -42=-42;
4(-1)-9*6+10*3+3(-5)=-43; -43=-43;
2(-1)-7*6- -(-5)=-39; -39=-39;
-1+5*6-2*3 =23; 23=23.
![]() или
или ![]()
Задание 93.
Дана матрица А . Требуется найти: 1) матрицу, обратную матрице А;
2) собственные значения и собственные векторы матрицы А.
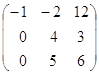
Решение:
| -1 | -2 | 12 | 1 | 0 | 0 | 1 | 2 | -12 | -1 | 0 | 0 | |||
| 0 | 4 | 3 | 0 | 1 | 0 | 0 | 4 | 3 | 0 | 1 | 0 | |||
| 0 | 5 | 6 | 0 | 0 | 1 | 0 | 5 | 6 | 0 | 0 | 1 | |||
| 1 | 0 | -13,5 | -1 | -0,5 | 0 | 1 | 0 | 0 | -1 | -8 | 6 | |||
| 0 | 1 | 0,75 | 0 | 0,25 | 0 | 0 | 1 | 0 | 0 | 6/9 | -3/9 | |||
| 0 | 0 | 2,29 | 0 | -1,25 | 1 | 0 | 0 | 1 | 0 | -5/9 | 4/9 | |||
Обратная матрица:
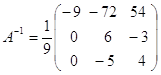
Корни характеристического уравнения:
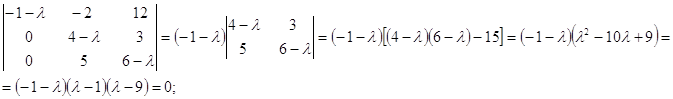
![]() - собственные значения матрицы А .
- собственные значения матрицы А .
При ![]()
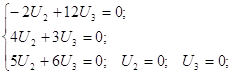
Собственный вектор:
![]()
Задание 103.
Построить график функции y=f(x) деформацией и сдвигом графика функции y=sin x.
![]()
Решение:
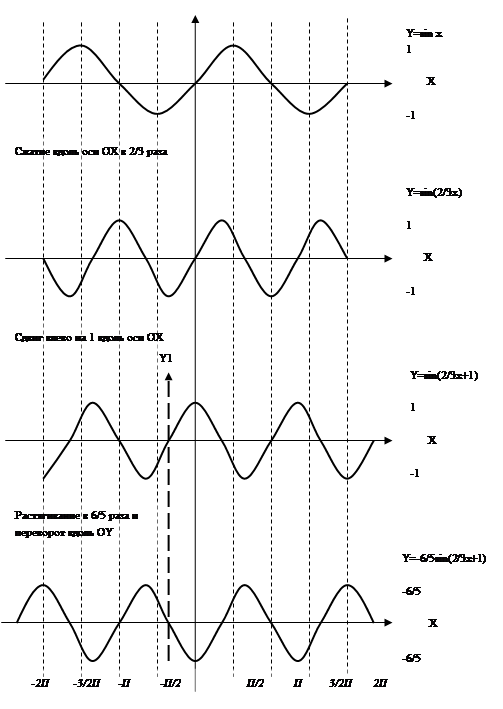
Задание 113.
Найти указанные пределы (не пользуясь правилом Лопиталя).
![]()
![]()
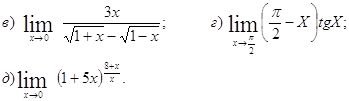
Решение:
![]()
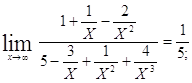
![]()
![]()
![]()
![]()
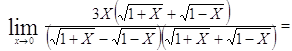
![]()
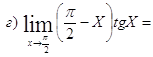
Подстановка: ![]()
![]()
![]()
![]()
![]()
Задание 123.
Дана функция y=f(x) и три значения аргумента x1,x2,x3. Установить, является ли эта данная функция непрерывной или разрывной для каждого из данных значений Х. Построить (приближенно) график функции в окрестностях каждой из данных точек.
![]()
Решение:
![]()
![]()
![]()
Так как ![]()
![]() ,то функция в точке Х1=-1 непрерывна.
,то функция в точке Х1=-1 непрерывна.
![]()
![]()
![]()
![]()
Так как ![]()
![]() ,то функция в точке х=3 разрывная.
,то функция в точке х=3 разрывная.
![]()
![]()
Так как ![]()
![]() ,то функция в точке х=7 непрерывна.
,то функция в точке х=7 непрерывна.
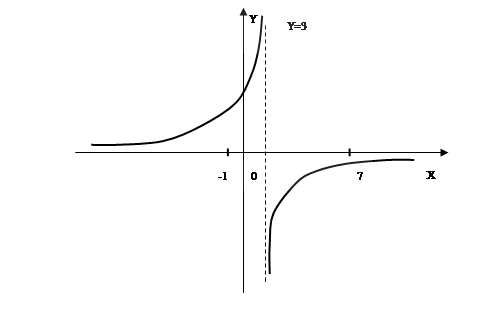
Задание 133.
Функция y=f(x) задана различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Построить график.
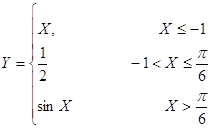
Решение:
![]()
![]()
![]()
![]()
Так как ![]()
![]() , то функция в точке х=-1 разрывна.
, то функция в точке х=-1 разрывна.
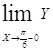
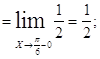
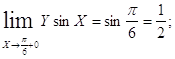
Так как 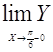
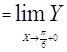 , то функция в точке
, то функция в точке ![]() непрерывна.
непрерывна.
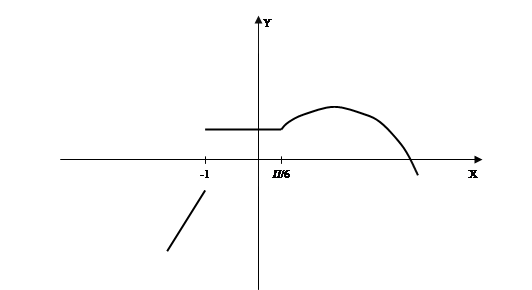
Задание 143.
Найти производные ![]()
![]() a)
a) ![]() б)
б) ![]() в)
в) ![]()
г) ![]() д)
д) ![]()
Решение.
а) ![]()
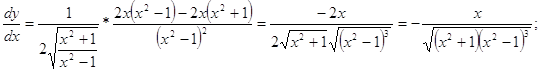
б) ![]()
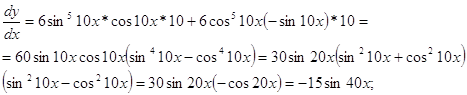
в) ![]()
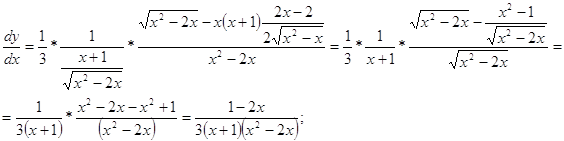
г) ![]()
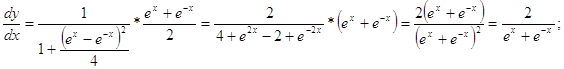
д) ![]()

Задание 153.
Найти ![]() для функции, заданной параметрическим.
для функции, заданной параметрическим.
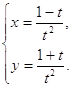
Решение.
![]()
![]()
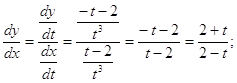
![]()
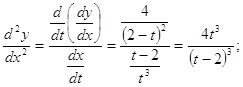
Задание 163.
На линии ![]() найти точку, в которой касательная к этой линии параллельна прямой
найти точку, в которой касательная к этой линии параллельна прямой ![]()
![]()
Решение.
Угловой коэффициент прямой:
![]() или
или ![]()
![]()
![]()
Угловой коэффициент касательной к линии:
![]()
Так как касательная к линии и прямая параллельны, то ![]()
тогда:
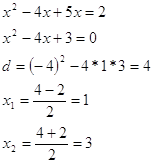
Таким образом получаются две точки:
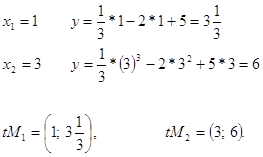
Задание 173.
Какова должна быть высота равнобедренного треугольника, вписанного в окружность диаметра d, чтобы площадь треугольника была наибольшей?
Решение.
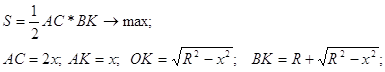
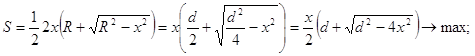
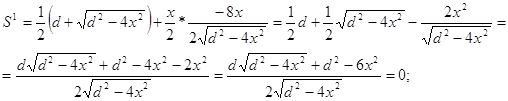
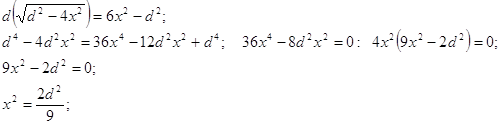
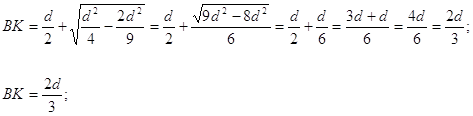
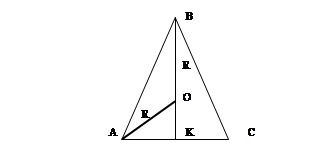
Задание 183.
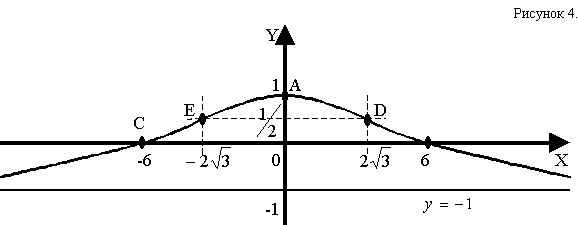
Исследовать методами дифференциального исчисления и построить график.
![]()
![]()
![]()
Решение.
![]()
1. область определения функции: ![]()
![]()
![]()
так как ![]()
![]() то функция нечетная.
то функция нечетная.
2. Точки пересечения с осями координат:
При ![]() при
при ![]()
![]()
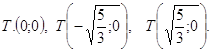
3. Область возрастания (убывания) функции, точки экстремумов:
![]()
При ![]() функция возрастает.
функция возрастает.
При ![]()
![]() функция убывает.
функция убывает.
При ![]() функция убывает.
функция убывает.
При ![]()
![]() функция возрастает
функция возрастает
![]()
Точка ![]() точка максимума.
точка максимума.
Точка ![]() точка минимума.
точка минимума.
Похожие работы
... факт; доказательство получается с помощью обратной процедуры.) Принято считать, что последователи Платона изобрели метод доказательства, получивший название «доказательство от противного». Заметное место в истории математики занимает Аристотель, ученик Платона. Аристотель заложил основы науки логики и высказал ряд идей относительно определений, аксиом, бесконечности и возможности геометрических ...
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... ; U’V+UV’+UV*P(x)=Q(x) ; U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 : Тогда U’V=Q(x) y’+y cos(x)=1/2 sin(2x) y=UV U’V+UV’+UVcos(x)=sin(x)cos(x) V’+Vcos(x)=0 dV/V=-cos(x)dx ln(V)= -sin(x) V=e-sin(x) sin(x)=t Билет №22 Уравнение Бернулли и Рикотти и их решение. Уравнение Бернулли – это диф. Ур-е следующего вида : где P(x) и Q(x) – непрерывные функции m – ...
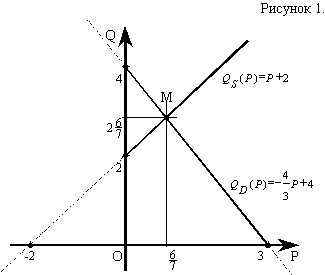
ние месяца, не выходящих в рейс из-за профилактического ремонта автомашин. дней в месяц каждый водитель из штата гаража не выходит в рейс из-за профилактического ремонта автомашин. Ответ:Каждый водитель из штата гаража в течение месяца может иметь свободных дней. Задание №3. Вопрос №1. Построить график функции спроса Q=QD(P) и предложения Q=QS(P) и найдите координаты точки равновесия, если , ...
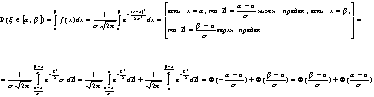
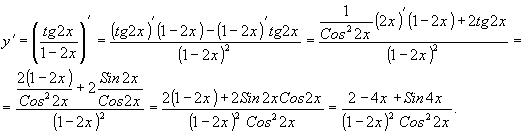
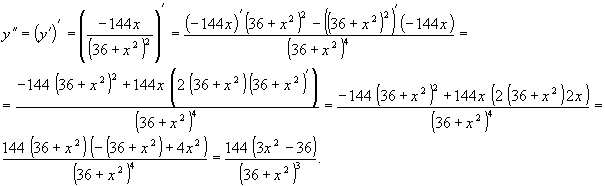
0 комментариев