Навигация
Область выпуклости (вогнутости) функции, точки перегибов
4. Область выпуклости (вогнутости) функции, точки перегибов.
![]()
При ![]() функция выпукла;
функция выпукла;
При ![]() функция вогнута;
функция вогнута;
При ![]() функция выпукла;
функция выпукла;
При ![]()
![]() функция вогнута.
функция вогнута.
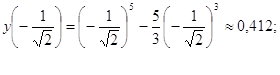

Точки ![]() - точки перегибов.
- точки перегибов.
5. Асимптот нет
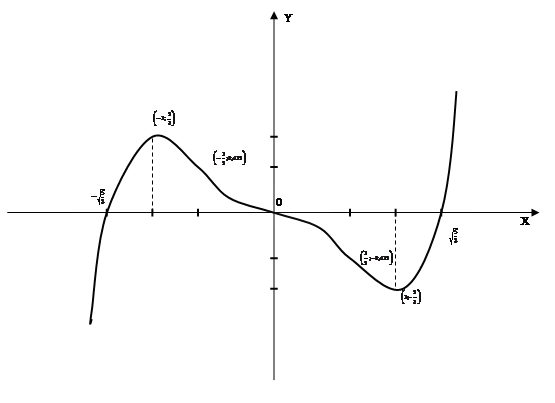
![]()
![]()
1. область определения функции: ![]()
2. точки пересечения с осями координат:
При ![]()
![]() так как
так как ![]() то функция нечетная.
то функция нечетная.
3. области возрастания (убывания) функции; точки экстремумов.
![]()
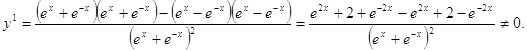
Точек экстремумов нет.
Так как ![]() то функция возрастает.
то функция возрастает.
4. область выпуклости (вогнутости) функции; точки экстремумов.
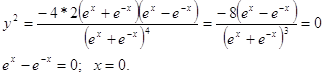
При ![]()
![]() функция вогнута;
функция вогнута;
При ![]() функция выпукла;
функция выпукла;
Точка (0;0) точка перегиба.
5. асимптоты.

![]() асимптота.
асимптота.![]()
![]()

Задание 193.
Определить количество действительных корней уравнения ![]() ;
;
отделить эти корни и, применяя метод хорд и касательных, найти их приближенные значения с точностью до 0,001.
![]()
Решение.
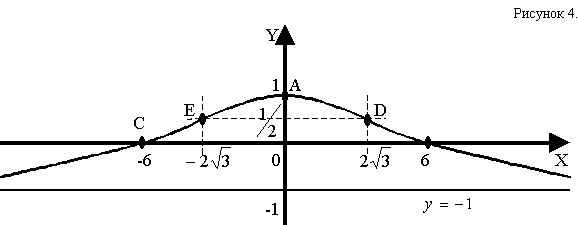
Исследуем график функции.
![]()
Количество корней К=1.
![]()
Таким образом, функция принимает значения на отрезке ![]() ,в качестве начального приближения возьмем
,в качестве начального приближения возьмем ![]()
метод касательных:
составим таблицу:
|
|
|
|
|
|
|
|
| 1 2 3 | -0,1 -0,398 -0,388 | -0,001 -0,063 -0,586 | 1,499 -0,053 -0,0001 | 5,03 5,475 5,452 | 0,298 -0,0097 -0,00002 | -0/3980 -0,3883 -0,3882 |
Искомый корень х=-03882
Задание 203.
Найти частные производные функции ![]()
![]()
Решение.
Частные производные:
![]()
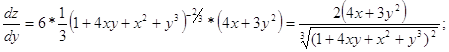
Задание 213.
Дана функция ![]() и две точки
и две точки ![]() . Требуется:
. Требуется:
1) вычислить приближенное значение функции у точке В, исходя из значения в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 2) вычислить точное значение функции в точке В и оценить в процентах относительную погрешность, возникающую при замене приращения функции дифференциалом.
![]()
Решение.
![]()
Вычислим частные производные в точке А.
![]()
![]()
![]()
![]()
Приближенное значение:
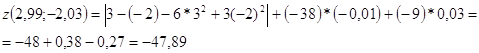
Вычислим точки значения функции:
![]()
![]()
Относительная погрешность вычисления:
![]()

Задание 223.
Даны функция ![]() точка
точка ![]() и вектор а. Требуется найти:
и вектор а. Требуется найти:
1) grad z в точке А; 2)производную по направлению вектора в точке А.
![]()
Решение.
1) вектором градиентом функции двух переменных ![]() является вектор:
является вектор:
![]()
![]()
Найдем частные производные в точке А:
![]()
![]()
![]()
2) производная по направлению вектора ![]() вычисляется по формуле.
вычисляется по формуле.
![]()
![]()
![]()
Задание 233.
Найти наименьшее и наибольшее значение функции ![]() в замкнутой области, ограниченной заданными линиями.
в замкнутой области, ограниченной заданными линиями.
![]()
Решение.
Частные производные:
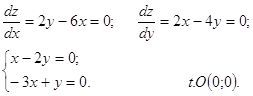
На прямой АВ: ![]() \
\
![]()
![]()
На прямой АС: ![]()
![]()
На прямой ВС: ![]()
![]()
![]()
![]()
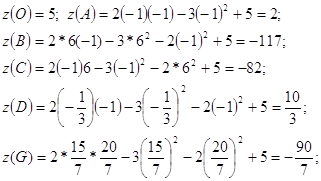
Z наибольшее =5; z наименьшее =-117.

Использованная литература:
1 Ткачук В.В. Математика абитуриенту:-М:МЦНМО,2002 г.
2 Сканави М.И. 2500 задач по математике для поступающих в вузы:
-М: Оникс 21 век, 2005 г.
3 Мельников И.И. Как решать задачи по математике на вступительных экзаменах. 3-е издание, переработанное: учебник/ И.И Мельников, И.Сергеев.-М:УНЦДО, 2004 г.
Похожие работы
... факт; доказательство получается с помощью обратной процедуры.) Принято считать, что последователи Платона изобрели метод доказательства, получивший название «доказательство от противного». Заметное место в истории математики занимает Аристотель, ученик Платона. Аристотель заложил основы науки логики и высказал ряд идей относительно определений, аксиом, бесконечности и возможности геометрических ...
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... ; U’V+UV’+UV*P(x)=Q(x) ; U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 : Тогда U’V=Q(x) y’+y cos(x)=1/2 sin(2x) y=UV U’V+UV’+UVcos(x)=sin(x)cos(x) V’+Vcos(x)=0 dV/V=-cos(x)dx ln(V)= -sin(x) V=e-sin(x) sin(x)=t Билет №22 Уравнение Бернулли и Рикотти и их решение. Уравнение Бернулли – это диф. Ур-е следующего вида : где P(x) и Q(x) – непрерывные функции m – ...
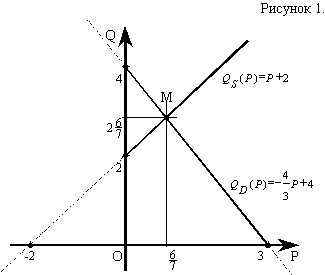
ние месяца, не выходящих в рейс из-за профилактического ремонта автомашин. дней в месяц каждый водитель из штата гаража не выходит в рейс из-за профилактического ремонта автомашин. Ответ:Каждый водитель из штата гаража в течение месяца может иметь свободных дней. Задание №3. Вопрос №1. Построить график функции спроса Q=QD(P) и предложения Q=QS(P) и найдите координаты точки равновесия, если , ...
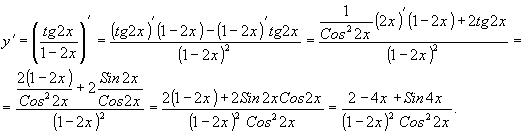
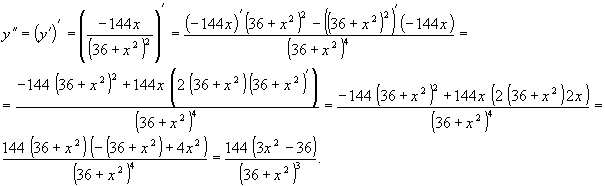
0 комментариев