Навигация
Основні поняття логіки предикатів
34324
знака
8
таблиц
0
изображений
2.1. Основні поняття логіки предикатів.
Як уже відзначалось під час вивчення логіки висловлювань, існують речення, які не є висловлюваннями та містять змінні. Був наведений приклад речення "х+1=3". Речення зі змінними не є висловлюваннями, але перетворюються в них, якщо надати значення змінним. Речення зі змінними дуже поширені. Вони містяться в математичних формулах та комп'ютерних програмах. Зокрема, у мовах програмування зустрічаються оператори такого змісту "повторювати цикл доти, поки змінні х та у не стануть рівними, або припинити обчислення циклу після 100 повторень". Якщо позначити через і лічильник повторень, то умова закінчення програми задаватиметься виразом "(x=y)
(i>100)", а сам оператор матиме вигляд "повторювати, якщо (¬((x=y)(i>100)))"
Приклад 2.1. Прикладами речень, які містять змінні є "х>3", "x=y+3", "x+у=z". Ці речення ні істинні, ні фальшиві доти, поки змінні не одержать значення.
У наведеному прикладі речення "х>3", або, в іншій формі, "х більше 3" складається з двох частин: першу, змінну х, називають предметом, другу - "більше 3", - яка вказує властивість предмета, називають предикатом. Часто предикатом називають все речення.
Уведемо логіку першого ступеня (логіку предикатів), в якій до понять логіки висловлювань додано нові поняття. Для формулювання складних думок у логіці висловлювань уведено атоми як основні елементи, з яких будують формули. Атом розглядався як неподільне ціле - його структура та склад не аналізувались. У той же час існує багато міркувань, які неможливо описувати лише за допомогою висловлювань. Тому введемо поняття атома у логіці першого ступеня. Для запису атомів логіки першого ступеня використовують такі типи символів:
1) Індивідні символи або сталі - це імена об'єктів, які починаються з великої букви: Іван, Марія та сталі: Т, F або 3.
2) Предметні символи - імена змінних, які позначають малими буквами, можливо, з індексами: х,у,z,vi,wj.
3) Предикатні символи — імена, якими позначають предикати та записують великими буквами: Р, Q, R, або змістовними словами, які записують великими буквами БІЛЬШЕ, ЛЮБИТЬ тощо.
Приклад 2.2. Позначимо речення "х більше 3" через Р(х), де предикатний символ Р позначає предикат "більше 3", а х - змінна, або предметний символ. Вираз Р(х) у цілому теж називають предикатом. Щоб записати твердження "х більше 3" як предикат, можна поступити інакше - визначити предикат БІЛЬШЕ(х,у), який означає "х більше y". Тоді речення "х більше 3" можна записати за допомогою предиката БІЛЬШЕ(х, 3).
Загалом, предикат, який містить n змінних: x1, x2, x3,…, xn, записують Р(х1,х2,...,хn) та називають n-місним. Змінну xi
Di(i=1,2,..,n) називають предметною, множину Di - її предметною областю, а символ Р - n-місним предикатним символом. Замість терміну "предикат" іноді використовують "пропозиційна функція".
Щойно змінна х дістає значення з предметної області, предикат Р(х) набуває значення Т або F та перетворюється у висловлювання. Аналогічно, якщо всі змінні багатомісного предиката одержать значення, то він набуде значення істинності й теж перетвориться у висловлювання.
Атом логіки першого ступеня має вигляд Р(х1, х2,...,хn), де Р- предикатний символ, а x1,x2,…,xn - предметні або індивідні символи.
Приклад 2.3. Нехай вираз "x+у=2" задано предикатом Q(х, у). Тоді Q(1,2) - фальшиве висловлювання, а Q(2,0) - істинне. Позначимо це так: Q(1,2)=F, Q(2,0)=Т. Задамо речення "х любить y" предикатом ЛЮБИТЬ(х,у). Тоді істинне речення "Іван любить Марію" подається істинним висловлюванням ЛЮБИТЬ (Іван, Марія).
Приклад 2.4. Якщо БІЛЬШЕ(х, у) - предикат, визначений у прикладі 2.2, то БІЛЬШЕ(5,3) - істинне висловлювання, а БІЛЬШЕ (1,3) - фальшиве висловлювання.
Існує інший шлях перетворення предиката у висловлювання - квантифікація. Нехай Р(х) — предикат, D — задана предметна область та хD. Використаємо два спеціальні символи 
та 
, які називають: - квантором загальності, - квантором існування. Якщо х - змінна, то вираз (х) читають "для всіх х", "для кожного х" або "для будь-якого х". Запис (х)Р(х) означає "Р(х) істинний для всіх значень х з предметної області" та читають "Р(х) для всіх х". Вираз (х) читають "існує х", "для деяких х" або "принаймні для одного х". Запис (х)Р(х) має зміст "в області D існує таке х, що Р(х) - істинний", або "в області D існує принаймні одне х таке, що Р(х) - істинний" або "Р(х) істинний для деякого х з області D. У подальшому в записі квантора будемо випускати дужки, записуючи х та х замість (х) та (х), відповідно.
Правильно побудовані формули логіки першого ступеня, або формули визначають так.
1. Атом є формулою.
2. Якщо H та G - формули, то (¬H),(H
G),(HG),(H→G) та (H~G) - формули.
3. Якщо H формула, а х - змінна у формулі H, то хH та хH - формули.
4. Формули одержують лише скінченною кількістю застосувань правил 1-3.
Наведемо приклади висловлювань, одержаних із застосуванням кванторів.
Приклад 2.5. Позначимо речення "х просте число" через P(х), "х раціональне число" - через Q(х), "х дійсне число" - через R(х) та "х менше y" - через МЕНШЕ(х, у). Розглянемо такі істинні речення.
1. Кожне раціональне число є дійсним.
2. Існує число, яке є простим.
3. Для кожного числа х існує таке число у, що х < у.
Наведені речення записують такими формулами.
1. x (Q(x) → R(x)).
2. x P(x)
3. xy МЕНШЕ(x, y)
Перехід від Р(х) до х Р(х) або х Р(х) називають зв'язуванням змінної x, а змінну х — зв'язаною. Не зв'язану змінну називають вільною. У формулах х Р(х) та х Р(х) предикат Р(х) перебуває в області дії відповідного квантора.
Приклад 2.6. У формулі х Р (х, у) змінна х зв'язана, а змінна у - вільна, оскільки перед формулою відсутній квантор, який містить цю змінну.
У разі знаходження значення істинності висловлювання, отриманого з пропозиційної функції зв'язуванням її змінних кванторами, важливе значення має предметна область.
Зв'язування частини змінних багатомісного предиката перетворює його в предикат меншої місності. Зміст зв'язаних і вільних змінних у предикатах різний. Вільні змінні - це звичайні змінні, які можуть приймати різні значення з предметної області D: значення виразу Р(х) залежить відзначення х. Формули х Р(х) і х Р(х) не залежать від змінної х та при визначених Р і D мають конкретні значення. Це, зокрема, означає, що перейменування зв'язаних змінних, а саме, заміна х Р(х) на у Р(у), не змінює значення істинності формули.
Похожие работы
... його функцій і структури, тобто ролі і значення в пізнанні і практичній діяльності, і в той же час з погляду складових його елементів, а також зв'язків і відносин між ними. Це і є власний, специфічний предмет логіки. Тому вона визначається як наука про форми і закони правильного мислення, що веде до істини. Що ж таке логічна культура? Це культура мислення, що виявляється в культурі письмового й ...
... (логіці, етиці і політиці) означає не що інше, як повернення до традиціоналістсько-авторитарного типу цивілізації, на що і претендував тоталітаризм XX в. 3. Загальне і відмінності формальної і діалектичної логіки В четвертій книзі “Метафізики" Арістотель ставив питання: який принцип є таким самоочевидним, що його можна покласти в основу істинної філософії. Таким самоочевидним принципом Арі ...
... , сполучників, префіксів і префіксальних словоформ, розділових знаків, а також за розподілом довжини речення). Крім статистичних методів, у мовознавстві застосовують методи теорії інформації, математичної логіки, теорії ймовірностей і теорії множин. 3. Застосування математичних теорій. Дані теорії інформації використовуються для найекономнішої передачі інформації засобами мови. Кожна ...
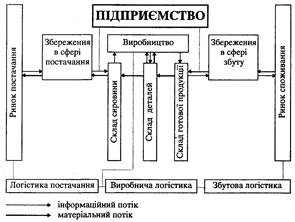
... і продукції. Виробничі потужності ТОВ «Брусилівський маслозавод» дозволяють виробляти близько 150 т масла, 30 т глазурованих сирків за рік, переробляючи приблизно 1000 кг молока за день. Основні споживачі продукції ТОВ «Брусилівський маслозавод» - населення Брусилівсьекого району та районів, що знаходяться поруч з Брусилівським, Житомирської області. . Отже, ТОВ «Брусилівський маслозавод» – ...
0 комментариев