Навигация
Закон розподілу ймовірностей випадкових величин
2. Закон розподілу ймовірностей випадкових величин
В результаті досліду неперервна випадкова величина X приймає одне із своїх можливих значень. Тобто з'явиться одна подія із повної групи несумісних подій: X = х1, X = Х2, ..., X — хn. Кожне із цих значень володіє ймовірністю появи, або
![]() ,
, ![]() , ...
, ... ![]()
Так як всі можливі події утворюють повну групу несумісних подій, то сума ймовірностей всіх можливих значень випадкової величини X дорівнює одиниці
![]()
Цілком зрозуміло, що випадкова величина буде повністю визначена, якщо вказати ймовірність кожної із подій.
Законом розподілу випадкової величини називають всяке співвідношення, що встановлює зв'язок між можливими значеннями випадкової величини і відповідними ймовірностями.
Закон розподілу дискретної випадкової величини задають:
1) аналітично;
2) чисельно у вигляді таблиці;
3) графічно.
Аналітично закон розподілу для дискретних випадкових величин задають за допомогою формул розподілу ймовірностей при повторних випробуваннях. Ймовірність появи k-ої події при n - випробуваннях розраховують за формулою.
Найбільш просто закон розподілу дискретної випадкової величини X відображають у вигляді таблиці, яку називають рядом розподілу випадкової величини.
Наочно ряд розподілу відображають графічно. Для цього можливі значення випадкової величини Х1 відкладають по осі абсцис, а по осі ординат - відповідні їм імовірності Р. Отримані вершини ординат з'єднують відрізками прямих ліній. Такий рисунок називають багатокутником розподілу.
Слід пам'ятати, що з'єднання вершин ординат проводиться тільки для більш наочного відображення. При цьому, в відрізках поміж Х1 і Х2, Х2 і X3 і далі, випадкова величина х немає значення і ймовірності її на цих відрізках дорівнюють нулю. Другою властивістю багатокутника розподілу є те, що сума ймовірностей всіх можливих значень випадкової величини (сума ординат) завжди дорівнює одиниці. Це виходить з того, що всі можливі значення випадкової величини X утворюють повну групу подій, сума ймовірностей яких дорівнює одиниці.
Немає сумніву, що ряд розподілу чи багатокутник розподілу можна подати для дискретної випадкової величини з кінцевим числом можливих значень. Однак ряд розподілу не можна побудувати для неперервної випадкової величини, що має незчисленну безліч можливих значень, які суцільно заповнюють деякий відрізок. Перелічити таку безліч значень випадкової величини практично неможливо. Проте, треба мати таку характеристику розподілу ймовірностей, яка б відображала як дискретні, так і неперервні випадкові величини. Нею є функція розподілу.
Функцією розподілу або інтегральним законом розподілу випадкової величини X називається задання ймовірності події виконання нерівності X < х, де х - деяка поточна змінна, її розглядають як функцію аргументу х і визначають за формулою
F(x) = P(X<x)
Функцію розподілу F(х) називають інтегральною функцією розподілу або інтегральним законом розподілу. Вона має досить просту геометричну інтерпретацію. Розглянемо випадкову величину, як випадкову точку X осі ОХ, що в результаті випробування може прийняти те чи інше положення. Тоді функція розподілу F(х) є ймовірністю того, що випадкова точка X в результаті випробування попаде зліва від точки х.
Функція дискретної випадкової величини X, що може приймати значення Х1,Х2, ... , xn буде мати вигляд
![]()
При цьому додавання ймовірностей розповсюджується на всі можливі значення випадкової-величини, які за своєю величиною менші аргументу х. Це означає, що функція розподілу дискретної випадкової величини X розривна і зростає стрибками при переході через точки можливих її значень Х1, Х2, ... , хn.
Оскільки функція розподілу дискретної випадкової величини виглядає як сходинкова ламана лінія, тому її називають сходинковим графіком.
Якщо випадкова величина неперервна, то вона має ймовірність в кожній точці осі х. Згідно з формулою функція розподілу буде зростати поступово, тому що можливі значення випадкової величини неперервно заповнюють будь-який інтервал на осі х. Тоді графік виглядатиме як монотонне зростаюча функція розподілу F(х) на інтервалі від а до b.
Функція розподілу має властивості:
1. Функція розподілу F(х) є зростаючою і міститься між нулем та одиницею 0 < F(х) < 1.
Це випливає з того, що функція F(х) визначається як імовірність випадкової події X < х.
2. Ймовірність виникнення випадкової величини в інтервалі від ![]() до
до ![]() дорівнює різниці значень функції на кінцях інтервалу
дорівнює різниці значень функції на кінцях інтервалу
![]()
Визначимо подію А того, що випадкова величина х < ![]() та подію В для випадку х <
та подію В для випадку х < ![]() .
.
Подія С відображає те, що ![]() < х <
< х < ![]() . В цьому випадку подія В буде складатися із суми двох несумісних подій А і С, тобто В = А + С. Згідно з теоремою додавання ймовірностей маємо
. В цьому випадку подія В буде складатися із суми двох несумісних подій А і С, тобто В = А + С. Згідно з теоремою додавання ймовірностей маємо
P (B) = P(A) + P(C)
Якщо функція в точці ![]() неперервна, то граничне значення дорівнює нулю. При розриві функції в точці (X її граничне значення буде дорівнювати значенню стрибка функції F (х).
неперервна, то граничне значення дорівнює нулю. При розриві функції в точці (X її граничне значення буде дорівнювати значенню стрибка функції F (х).
З цього робимо висновок, що ймовірність випадкової величини в точці для неперервної функції дорівнює нулю. Це явище називають парадоксом теорії ймовірностей.
Проте нульова ймовірність події лише зазначає, що частота цієї події невпинно спадає при збільшенні числа дослідів, однак це не означає, що ця подія неможлива.
3. Функція розподілу випадкової величини є зростаючою функцією, тобто при ![]() >
> ![]()
![]()
Маємо ![]()
Так як імовірність будь-якої події є додатне число, то ![]()
3. На мінус нескінченності функція розподілу дорівнює нулю, а на плюс нескінченності - одиниці, тобто ![]()
![]()
Це цілком вірно, так як при необмеженому переміщенні точки х вліво, попадання випадкової точки X лівіше х максимально стає неможливою подією і ![]() = 0. В той же час при необмеженому переміщенні точки х вправо попадання випадкової точки X зліва від х практично стає достовірною подією, тоді
= 0. В той же час при необмеженому переміщенні точки х вправо попадання випадкової точки X зліва від х практично стає достовірною подією, тоді ![]() = 1.
= 1.
За допомогою функції розподілу можна знайти ймовірність випадкової величини в будь-якому інтервалі або в кожній точці можливих значень для дискретної випадкової величини. Тому функція розподілу однозначно визначає закон розподілу випадкової величини.
Більш наочно характер розподілу неперервної випадкової величини в невеликих інтервалах числової осі х дає функція щільності розподілу ймовірностей або диференціальний закон розподілу.
Якщо маємо функцію розподілу F(х) випадкової величини X, то ймовірність попадання її на елементарну ділянку (х, х + ![]() х) згідно з попередньою формулою буде:
х) згідно з попередньою формулою буде:
![]()
Знайдемо середню ймовірність, що припадає на одиницю довжини ділянки ![]() х
х
![]()
Функцією щільності розподілу випадкової величини в точці х є граничне відношення ймовірності попадання її на елементарну ділянку від х до х + ![]() х до довжини цієї ділянки
х до довжини цієї ділянки ![]() х, коли
х, коли ![]() х наближається до нуля.
х наближається до нуля.
Її позначають ![]() або (х). Зміст функції щільності розподілу
або (х). Зміст функції щільності розподілу ![]() (х) полягає в тому, що вона вказує, як часто з'являється випадкова величина X навколо точки х при повторенні дослідів.
(х) полягає в тому, що вона вказує, як часто з'являється випадкова величина X навколо точки х при повторенні дослідів.
Функція щільності розподілу має властивості:
1. Щільність розподілу невід'ємна, тобто ![]()
2. Функція розподілу випадкової величини дорівнює інтегралу від функції щільності в інтервалі від - ![]() до х
до х ![]()
3. Ймовірність попадання неперервної випадкової величини X на відрізку (![]() ) дорівнює інтегралу від функції щільності розподілу, взятому за кінцевими значеннями цього відрізка
) дорівнює інтегралу від функції щільності розподілу, взятому за кінцевими значеннями цього відрізка

Геометричний зміст цього результату полягає в тому, що ймовірність появи випадкової величини в інтервалі від ![]() до
до ![]() дорівнює площі криволінійної трапеції.
дорівнює площі криволінійної трапеції.
4. Інтеграл в нескінченних межах від - ![]() до +
до + ![]() дорівнює одиниці
дорівнює одиниці
![]()
Ймовірність попадання випадкової величини X на елементарний інтервал dx з точністю до нескінченно малих вищого порядку чим ![]() х дорівнює
х дорівнює ![]() (х) dх, (так як
(х) dх, (так як ![]() ). Геометричний зміст цього виявляється в тому, що це є площа елементарного прямокутника з висотою
). Геометричний зміст цього виявляється в тому, що це є площа елементарного прямокутника з висотою ![]() (х) і основою dх. Величина
(х) і основою dх. Величина ![]() називається елементом імовірності.
називається елементом імовірності.
Похожие работы
... і працездатності людини в процесі труда. Максимальне зменшення числа шкідливих впливів, створення комфорту — от головні задачі охорони праці. Тема дипломної роботи — “Моделювання процесу обробки сигналів датчика у вихровому потоковимірювачі”. Машинний зал ПЕОМ є помешканням з підвищеною небезпекою поразки людини електричним струмом, тому що в даному помешканні присутня можливість одночасного ...
... , що виявляються. Наслідком цього правила є необхідність застосування тим більше вдосконалених математичних методик, чим менш досконалі інші методи (фізичні, хімічні, фізіологічні, біохімічні тощо), які використовуються в медико-біологічних дослідженнях. Іншими словами, маючи можливість використовувати досить могутній математичний апарат, можливо спрощувати і скорочувати процес вивчення явища за ...
... фахівцями, в обов'язки яких не входить аналіз похибок результатів вимірювання. Для забезпечення необхідного рівня точності технічних вимірювань при їхньому виконанні користуються атестованими методиками виконання вимірювань, які розробляють висококваліфіковані спеціалісти - метрологи. Вимірювання ФВ за наявністю або відсутністю розмірності у вимірюваних величин поділяють на вимірювання розмірних ...
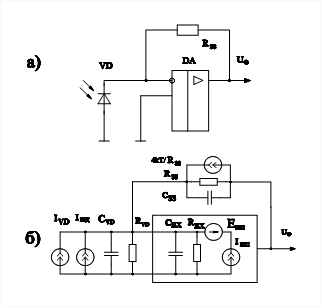
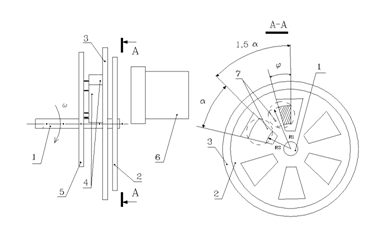
... дипломного проекту. Рисунок 3.1 – Схема електрична структурна пристрою контролю середнього значення кутової швидкості 4. Розробка принципової схеми комп’ютеризованої вимірювальної системи параметрів електричних машин з газомагнітним підвісом 4.1 Аналіз лінійного фотоприймача Фотоелектричні перетворювачі площа-напруга (ППН) використовуються у багатьох пристроях, таких як перетворювач ...




0 комментариев