Метод комплексных чисел в планиметрии

Предисловие

В данной работе рассмотрен метод комплексных чисел в планиметрии, применение его критериев в задачах элементарного характера на темы – «Параллельность, коллинеарность, перпендикулярность», «Углы и площади», «Многоугольники», «Прямая и окружность».

Метод комплексных чисел в иностранной литературе используется достаточно широко. Однако в отечественной литературе этот метод не получил широкого распространения. Имеются отдельные фрагменты в книге З. А. Скопеца. Систематическое изложение этого метода дано в книге Я. П. Понарина «Алгебра комплексных чисел в геометрических задачах». Нами выбраны и решены на наш взгляд наиболее интересные задачи, выполняемые этим методом.

Метод комплексных чисел позволяет решать планиметрические задачи прямым вычислением по готовым формулам. Выбор этих формул с очевидностью диктуется условием задачи и её требованием. В этом состоит необычайная простота этого метода по сравнению с векторным и координатным методами, методом геометрических преобразований, конструктивно-синтетическим методом, требующими от решающего порой немалой сообразительности и длительных поисков, хотя при этом готовое решение может быть коротким.

 

§ 1 Параллельность, коллинеарность, перпендикулярность.

1.1. Коллинеарность векторов.

(1.2)

1.2. Коллинеарность трёх точек.

(1.3)

Это – критерий принадлежности точек А, В, С одной прямой.

(1.5)

определяет прямую, содержащую хорду АВ единичной окружности.

1.3. Перпендикулярность отрезков (векторов).

  (1.7)

Уравнение касательной

(1.8)

(1.9)

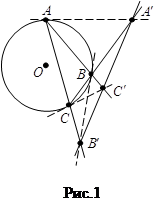
З а д а ч а 1. Доказать, что точки пересечения прямых, содержащих стороны треугольника, с касательными к описанной окружности в противоположных им вершинах коллинеарны.

  § 2 Углы и площади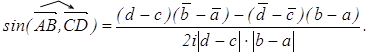

2.1. Угол между векторами.

(2.1)

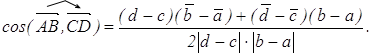
(2.2)

 

2.2. Площадь треугольника

(2.3)

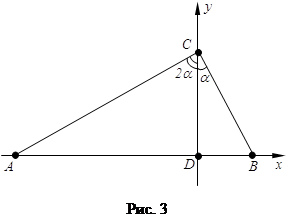
З а д а ч а 2. Основание D высоты CD треугольника ABC делит сторону AB в отношении 3:1. Угол ACD вдвое больше угла BCD. Вычислить углы треугольника ABC.

 

§ 3 Многоугольники

3.1. Подобные треугольники.

(3.1)

где  – комплексное число,  – коэффициент подобия.

(3.2)

где  – комплексное число,  – коэффициент подобия.

Если , то треугольники  и  равны. Тогда соотношение (3.1) – признак равенства одинаково ориентированных треугольников, а соотношение (3.2) – признак равенства противоположно ориентированных треугольников.

3.2. Критерий правильного треугольника.

Треугольник ориентирован положительно:

(3.4)

Треугольник ориентирован отрицательно:

(3.5)