Навигация
4.1. Уравнение прямой.
(4.1)
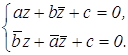
Пусть коэффициенты a и b не обращаются в нуль одновременно. Приходим к уравнению: 
которое а) имеет единственное решение при 
б) имеет бесконечное множество решений при 
Отсюда и на основании предыдущих исследований получаем, что уравнение (4.1) определяет а) единственную точку при б) прямую при 
в) пустое множество при 
4.3. Общее уравнение окружности в сопряжённых комлексных координатах. Окружность с центром S(s) и радиусом R имеет уравнение
(4.2)
где z – координата переменной точки окружности.
(4.4)
Сравнивая уравнение (4.3) с уравнением (4.2) приходим к выводу, что уравнения (4.3) и (4.2) задают окружность тогда и только тогда, когда 
и ab - c – действительное число. Отсюда 
, а значит, с должно быть действительным числом. Итак, уравнение
(4.5)
есть уравнение окружности с центром 
и радиусом 
4.4. Уравнение окружности по трём данным точкам. Пусть окружность 
проходит через точки A, B, C. Тогда однородная линейная система
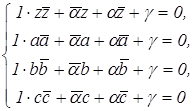
относительно 
имеет ненулевое решение (так как окружности определяются тремя неколлинеарными точками), поэтому её определитель равен нулю:
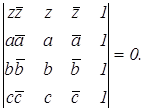(4.6)
Это уравнение представляет собой уравнение окружности по трём данным точкам.
4.5. Ортогональные окружности. Две пересекающиеся окружности называются ортогональными, если касательные к ним в их общей точке перпендикулярны. Очевидно, что касательная к одной из окружностей в их общей точке содержит центр другой окружности.
Даны две окружности (A,R) и (B,r), заданные соответственно уравнениями: 
где 
и 
где 
Для того, чтобы эти окружности были ортогональны, необходимо и достаточно, чтобы 
или
(4.7)
или
(4.8)
З а д а ч а 7. В плоскости даны два отрезка AB и CD. Найдите множество точек М, для каждой из которых площади треугольников MAB и MDC равны (рис. 10).
З а д а ч а 9. На гипотенузе AB прямоугольного треугольника ABC дана произвольная точка P. Докажите, что окружности, описанные около треугольников APC и BPC, ортогональны.
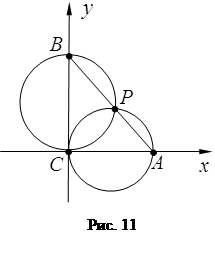Д о к а з а т е л ь с т в о. Примем вершину С данного треугольника за начальную точку. Пусть точкам А, В, P соответствуют комплексные числа 1, b, p, а центрам окружностей РАС и РВС числа 
(рис. 11). По условию 
или 
. Переходя к комплексным числам, получаем: 
откуда 
.
Руководствуясь (4.6), составим уравнение окружности РВС:
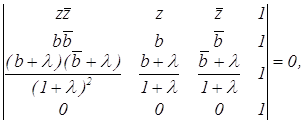
или
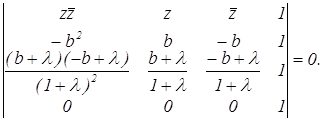
После раскрытия определителя получаем:
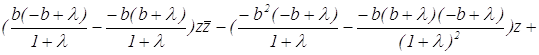
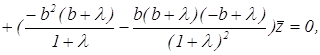
или
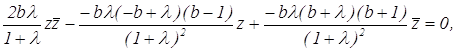
откуда
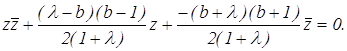
Из уравнения находим: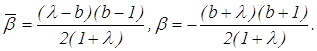 
Аналогично, для окружности РAС имеем:
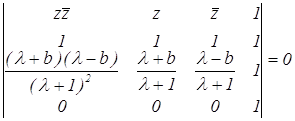
и
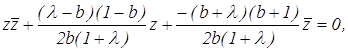
отсюда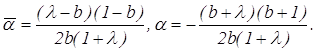 
Согласно критерию (4.8) для того, чтобы окружности РАС и РВС были ортогональны необходимо и достаточно, чтобы 
Учитывая предыдущие результаты, проверим выполнимость данного критерия:
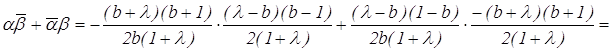
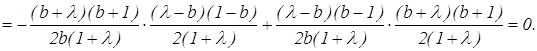
Таким образом, окружности РАС и РВС являются ортогональными.
Похожие работы
... 1. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD. (Рис.1)Доказать, что |AB|2+|BC|2+|CD|2+|DA|2 = |AC|2+|BD|2+4|MN|2.Решение. Пусть точкам A, В, С, D, М, N соответствуют комплексные числа а, b, с, d, т, п.Так как m = и n = , то |AB|2+|BC|2+|CD|2+|DA|2 |AC|2+|BD|2+4|MN|2 .Равенство доказано.Задача 2. Доказать, что если в плоскости параллелограмма ABCD существует такая точка М, ...
... , поскольку точки М и М’ входят в формулу равноправно, а для центра инверсии и бесконечно удаленной области все очевидно. 1.3. Формула инверсии в комплексно сопряженных координатах. Найдем формулу обобщенной инверсии при задании точек комплексными числами. Пусть точкам S, M и М’ соответствуют комплексные числа s, z и z’. По формуле скалярного произведения векторов . Коллинеарность точек S, M и ...
... . Частные случаи тригонометрических уравнений Определение. Уравнения вада sin x = a; cos x = a; tg x = a; ctg x = a, где x - переменная, aR, называются простейшими тригонометрическими уравнениями. Тригонометрические уравнения Аксиомы стереометрии и следствия из них Основные фигуры в пространстве: точки, прямые и плоскости. Основные свойства точек, прямых ...
... того материала, который имеется в учебнике, так организовать работу с детьми, чтобы она способствовала развитию пространственного мышления. Глава II. Методика формирования пространственного мышления учащихся основной школы при изучении векторного пространства 2.1 Методические аспекты развития пространственного мышления как элемента образного Рассмотрим, какие подходы предлагают для ...
0 комментариев