Навигация
Правильные многоугольники
6314
знаков
0
таблиц
13
изображений
3.3 Правильные многоугольники.
где k принимает значения 
. Все n значений 
имеют один и тот же модуль 
Корням уравнения
соответствуют вершины 
.
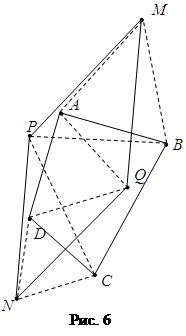З а д а ч а 3. Точки 
симметричны точке Р, лежащей в плоскости треугольника ABC, относительно, соответственно, прямых AB, BC, CA. Точки 
– середины отрезков 
Докажите, что треугольники 
и 
подобны и противоположно ориентированы (рис. 5).
З а д а ч а 4. На сторонах 
и 
выпуклого четырёхугольника 
вне его построены правильные треугольники 
и 
а на сторонах 
и 
построены правильные треугольники 
и 
лежащие с четырёхугольником в одной полуплоскости относительно прямых и соответственно. Докажите, что 
–параллелограмм (рис. 6).
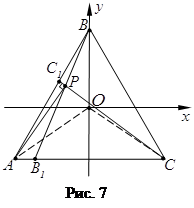
З а д а ч а 5. Точка 
делит сторону правильного треугольника 
в отношении 3:2 считая от точки 
. Точка 
делит сторону 
в отношении 3:14, считая от точки . Отрезки 
и 
пересекаются в точке
. Докажите, что прямые 
и перпендикулярны.
З а д а ч а 6. Через центр правильного треугольника проведена прямая. Доказать, что сумма квадратов расстояний от вершин треугольника до прямой не зависит от выбора прямой.
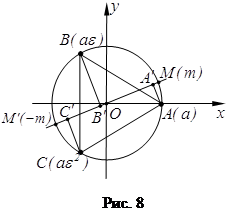
З а д а ч а 7. Пусть d – диаметр окружности, 
и
– стороны вписанного в неё и описанного около
неё правильных n-угольников. Докажите, что
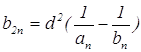(рис. 9).
Похожие работы
... 1. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD. (Рис.1)Доказать, что |AB|2+|BC|2+|CD|2+|DA|2 = |AC|2+|BD|2+4|MN|2.Решение. Пусть точкам A, В, С, D, М, N соответствуют комплексные числа а, b, с, d, т, п.Так как m = и n = , то |AB|2+|BC|2+|CD|2+|DA|2 |AC|2+|BD|2+4|MN|2 .Равенство доказано.Задача 2. Доказать, что если в плоскости параллелограмма ABCD существует такая точка М, ...
... , поскольку точки М и М’ входят в формулу равноправно, а для центра инверсии и бесконечно удаленной области все очевидно. 1.3. Формула инверсии в комплексно сопряженных координатах. Найдем формулу обобщенной инверсии при задании точек комплексными числами. Пусть точкам S, M и М’ соответствуют комплексные числа s, z и z’. По формуле скалярного произведения векторов . Коллинеарность точек S, M и ...
... . Частные случаи тригонометрических уравнений Определение. Уравнения вада sin x = a; cos x = a; tg x = a; ctg x = a, где x - переменная, aR, называются простейшими тригонометрическими уравнениями. Тригонометрические уравнения Аксиомы стереометрии и следствия из них Основные фигуры в пространстве: точки, прямые и плоскости. Основные свойства точек, прямых ...
... того материала, который имеется в учебнике, так организовать работу с детьми, чтобы она способствовала развитию пространственного мышления. Глава II. Методика формирования пространственного мышления учащихся основной школы при изучении векторного пространства 2.1 Методические аспекты развития пространственного мышления как элемента образного Рассмотрим, какие подходы предлагают для ...
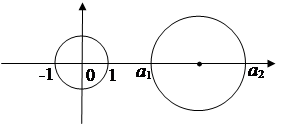
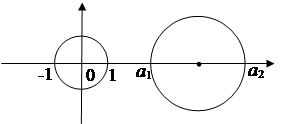
0 комментариев