Навигация
1.8 Оптимальный выбор шага
Предположим, что при интегрировании от точки ![]() до точки
до точки ![]() с шагом
с шагом ![]() погрешность приближенно равна
погрешность приближенно равна ![]() . Так как это соответствует росту погрешности со скоростью, приблизительно равной
. Так как это соответствует росту погрешности со скоростью, приблизительно равной ![]() , то
, то ![]() , где
, где ![]() – функция, определяющая шаг. Положим
– функция, определяющая шаг. Положим ![]() и получим оценку интеграла, который приближенно равен полной погрешности:
и получим оценку интеграла, который приближенно равен полной погрешности:
![]()
С другой стороны, затраты будут пропорциональны числу шагов, которое приближенно равно
![]()
Методами вариационного исчисления можно показать, что если мы хотим минимизировать затраты ![]() при некотором фиксированном значении погрешности
при некотором фиксированном значении погрешности ![]() , то следует сохранять постоянной величину
, то следует сохранять постоянной величину 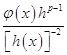 . Это означает, что окончательная погрешность должна быть одинаковой на каждом шаге.
. Это означает, что окончательная погрешность должна быть одинаковой на каждом шаге.
В современных программах[4], реализующих методы Рунге-Кутты, обязательно используется некоторый алгоритм автоматического изменения шага интегрирования. Интуитивно ясно, что на участках плавного изменения решения счет можно вести с достаточно крупным шагом. В то же время, на тех участках, где происходят резкие изменения поведения решения, необходимо выбирать мелкий шаг интегрирования. Обычно начальное значение шага задет пользователь или оно определено в программе. Далее шаг интегрирования изменяется в соответствии с величиной, получаемой в ходе вычисления оценки локальной погрешности.
Существует достаточно много способов оценки локальной погрешности, среди которых так называемое правило Рунге. Однако в моей программе я использовал самый простой и в то же время эффективный способ оценки локальной погрешности, который описан в разделе 3.1. «Описание программы Ilya RK-4 версия 1.43». Этот метод базируется на удвоении или делении пополам длины шага в зависимости от отношения локальной погрешности и максимально локальной допустимой погрешности ![]() .
.
2. Практическая часть
2.1 Описание программы «Ilya RK-4 версия 1.43»
Программа для нахождения интегральной кривой, удовлетворяющей поставленной задаче Коши написана на языке высокого уровня Borland C++ 3.1. Программа состоит из четырех функций. При помощи директив препроцессора #define определены максимальный шаг и величина локальной максимальной погрешности, а также номер версии программы. Рассмотрим подробнее работу программы в комплексе.Функция title() предназначена для печати на экране названия программы.
Функция do_step() совершает один шаг Рунге-Кутты и возвращает полученное значение. В качестве входных параметров в нее передается текущее положение, значение искомой функции, вычисленное на предыдущем шаге и величина шага, с которым требуется произвести шаг.
Функция f() задает правую часть дифференциального уравнения, левая часть дифференциального уравнения равна ![]() . В качестве аргументов функции передается
. В качестве аргументов функции передается ![]() и
и ![]() .
.
Функция main() – основная функция программы. У пользователя запрашивается точка, начиная с которой необходимо отобразить решение задачи Коши, точка, правая граница интегрирования и значение в левой точке, через которое обязана проходить искомая интегральная кривая. После этого программа начинает вычислительный процесс, выводя полученные значения на экран в виде списка и в текстовый файл “rk4.txt” на диск. После того, как будет достигнута правая граница интегрирования, процесс остановится и пользователю будет предложено нажать на любую клавишу для того, чтобы построить график. Для построения графика программа переключается в графический режим. График масштабируется с учетом того, чтобы он всегда был виден на экране вне зависимости от того, как высоко или низко от оси абсцисс он лежит. Кроме того, программа постарается сделать его максимально наглядным. Для этого будут проведены пунктирные линии, соответствующие минимальному и максимальному значению интегральной кривой, левому и правому концам интегрирования, а также значению интегральной кривой в указанной точке ![]() . Для того, чтобы пользователь мог легко ориентироваться на графике, рядом с пунктирными линиями пишутся координатные значения с точностью до двух десятичных знаков. Как показали многочисленные тесты, проведенные на компьютере на базе процессора Intel Pentium 4B с тактовой частотой 2.4 ГГц, построение графика происходит значительно быстрее, чем первичный расчет с выводом на экран и записью в файл. В этом легко убедиться[5], если задать довольно большой отрезок интегрирования, например [-100,100].
. Для того, чтобы пользователь мог легко ориентироваться на графике, рядом с пунктирными линиями пишутся координатные значения с точностью до двух десятичных знаков. Как показали многочисленные тесты, проведенные на компьютере на базе процессора Intel Pentium 4B с тактовой частотой 2.4 ГГц, построение графика происходит значительно быстрее, чем первичный расчет с выводом на экран и записью в файл. В этом легко убедиться[5], если задать довольно большой отрезок интегрирования, например [-100,100].
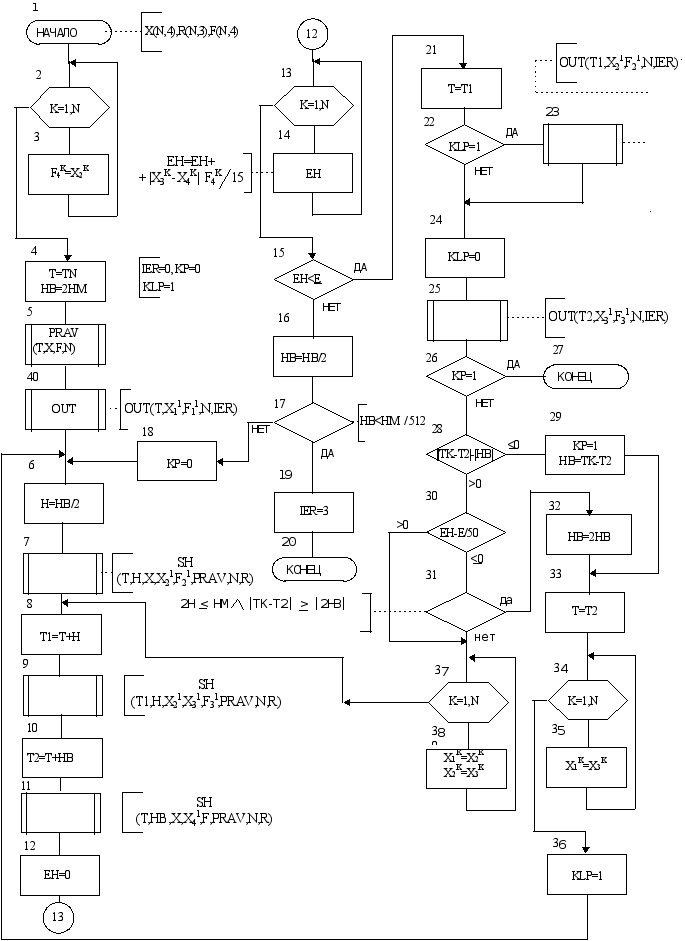
Программа применяет следующий метод Рунге-Кутты четвертого порядка.
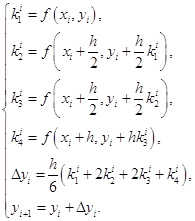
Для того, чтобы программа могла «разгоняться» после уменьшения шага, предусмотрено условие увеличения длины шага. Оно состоит в том, что если погрешность между вторым из двух значений, вычисленных с шагом ![]() и значением, вычисленным с шагом
и значением, вычисленным с шагом ![]() , не превосходит
, не превосходит ![]() , то шаг увеличивается вдвое и тело цикла повторяется. Отметим, что величина шага не может превосходить значения MAXSTEP, которое определяется директивой препроцессора #define. Если ни одно из двух описанных выше условий не выполняется, это означает, что шаг оптимален и программа производит вычисление значения функции с записью его в файл и отображением на экране.
, то шаг увеличивается вдвое и тело цикла повторяется. Отметим, что величина шага не может превосходить значения MAXSTEP, которое определяется директивой препроцессора #define. Если ни одно из двух описанных выше условий не выполняется, это означает, что шаг оптимален и программа производит вычисление значения функции с записью его в файл и отображением на экране.
Программа снабжена механизмом защиты от сбоев – в случае, если интегрируемая функция терпит разрыв (ее нельзя интегрировать на данном участке), программа останавливается и выдается сообщение о невозможности продолжать. Работоспособность этого механизма проверена на некоторых разрывных функциях, таких как тангенс и др.
Заключение
В работе детально рассмотрен метод Рунге-Кутты четвертого порядка с автоматическим выбором длины шага, приведены необходимые теоретические сведения, освещены альтернативные методы и их эффективность.
Был разработан алгоритм программного модуля, позволяющий автоматически менять величину шага интегрирования при решении задачи Коши в зависимости от требуемой точности, что является непременным требованием, предъявляемым ко всем хорошим современным программам данного класса, написано приложение, решены примеры.
Список использованных источников
[1]. Амоносов А.А., Дубинский Ю.А., Копченова Н.В. «Вычислительные методы для инженеров», М., Высшая школа, 1994, 544с.
[2]. Хайрер Э., Нёрсетт С., Ваннер Г. «Решение обыкновенных дифференциальных уравнений. Нежесткие задачи», М., Мир, 1990, 512с.
[3]. Холл Д., Уатт Д. «Современные численные методы решения обыкновенных дифференциальных уравнений», М., Мир, 1979, 312с.
Приложение А. Графики функций
В данном приложении рассмотрены три дифференциальных уравнения первого порядка. К каждому уравнению прилагается по два графика – первый из них построен созданным приложением, а второй создан в пакете Maple 9.01.
![]()
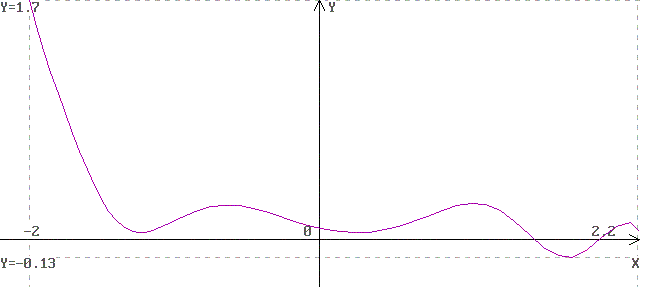
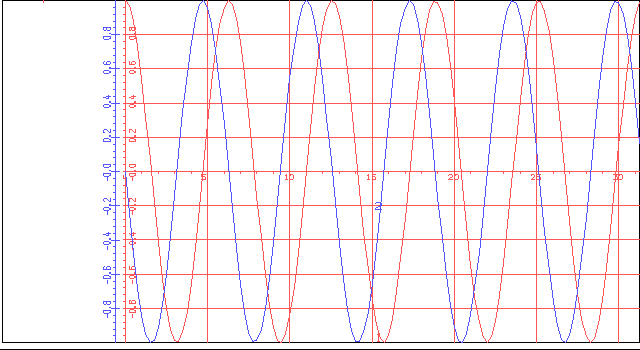
Интегральная кривая, построенная приложением «Ilya RK-4 версия 1.43»
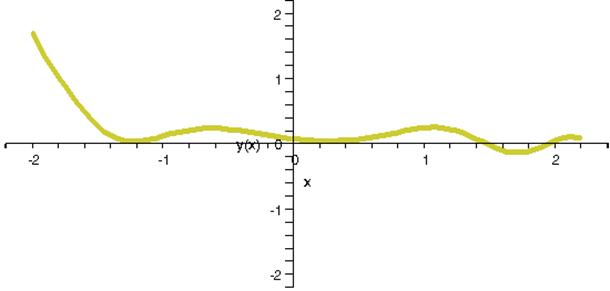
Интегральная кривая, построенная математическим пакетом Waterloo Maple 9.01
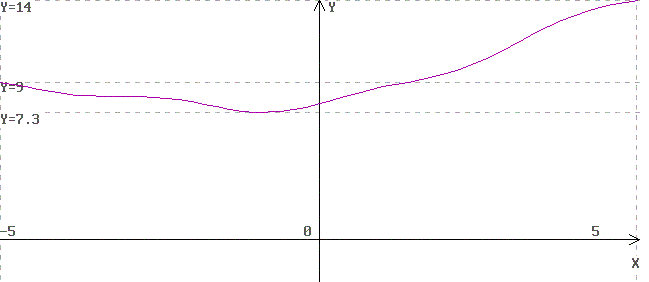
Интегральная кривая, построенная приложением «Ilya RK-4 версия 1.43»
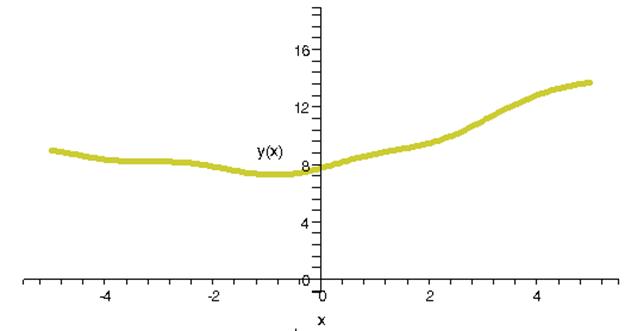
Интегральная кривая, построенная математическим пакетом Waterloo Maple 9.01
![]()
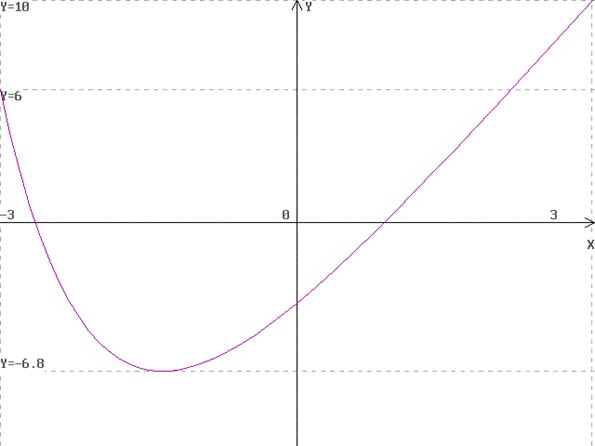
Интегральная кривая, построенная приложением «Ilya RK-4 версия 1.43»
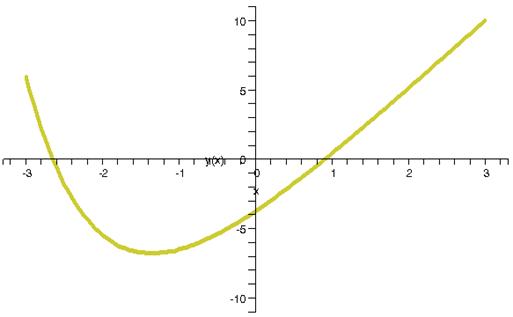
Интегральная кривая, построенная математическим пакетом Waterloo Maple 9.01
![]()
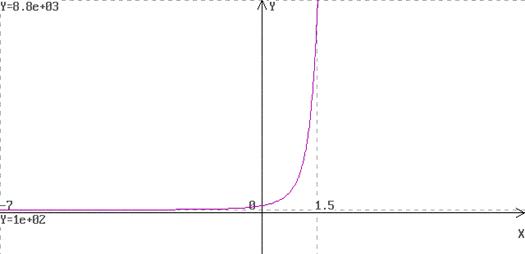
Интегральная кривая, построенная приложением «Ilya RK-4 версия 1.43»
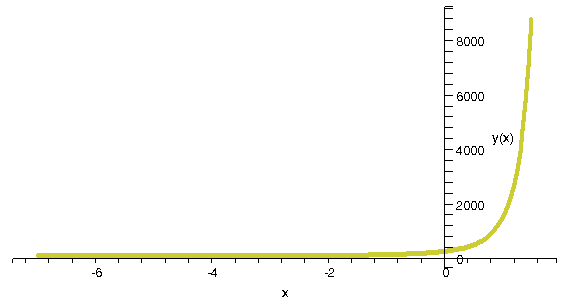
Интегральная кривая, построенная математическим пакетом Waterloo Maple 9.01
Приложение Б.
Пример таблицы значений функции y(x)y(-7)=100, h=0.4
y(-6.6)=100.045, h=0.4
y(-6.2)=100.112, h=0.4
y(-5.8)=100.212, h=0.4
y(-5.4)=100.361, h=0.4
y(-5)=100.585, h=0.4
y(-4.6)=100.919, h=0.4
y(-4.2)=101.419, h=0.4
y(-3.8)=102.17, h=0.4
y(-3.4)=103.301, h=0.2
y(-3.2)=104.067, h=0.2
y(-3)=105.011, h=0.2
y(-2.8)=106.175, h=0.2
y(-2.6)=107.615, h=0.2
y(-2.4)=109.4, h=0.2
y(-2.2)=111.62, h=0.2
y(-2)=114.392, h=0.2
y(-1.8)=117.873, h=0.2
y(-1.6)=122.267, h=0.2
y(-1.4)=127.857, h=0.2
y(-1.2)=135.033, h=0.2
y(-1)=144.346, h=0.2
y(-0.8)=156.596, h=0.2
y(-0.6)=172.977, h=0.1
y(-0.5)=183.256, h=0.1
y(-0.4)=195.327, h=0.1
y(-0.3)=209.595, h=0.1
y(-0.2)=226.578, h=0.1
y(-0.1)=246.953, h=0.05
y(-0.05)=258.68, h=0.05
y(2.96985e-15)=271.608, h=0.05
y(0.05)=285.897, h=0.05
y(0.1)=301.73, h=0.05
y(0.15)=319.32, h=0.05
y(0.2)=338.919, h=0.05
y(0.25)=360.821, h=0.05
y(0.3)=385.374, h=0.05
y(0.35)=412.989, h=0.05
y(0.4)=444.156, h=0.05
y(0.45)=479.459, h=0.025
y(0.475)=498.877, h=0.025
y(0.5)=519.603, h=0.025
y(0.525)=541.747, h=0.025
y(0.55)=565.433, h=0.025
y(0.575)=590.794, h=0.025
y(0.6)=617.978, h=0.025
y(0.625)=647.149, h=0.025
y(0.65)=678.489, h=0.025
y(0.675)=712.199, h=0.025
y(0.7)=748.501, h=0.025
y(0.725)=787.645, h=0.025
y(0.75)=829.906, h=0.025
y(0.775)=875.592, h=0.025
y(0.8)=925.047, h=0.025
y(0.825)=978.656, h=0.025
y(0.85)=1036.85, h=0.025
y(0.875)=1100.11, h=0.025
y(0.9)=1168.98, h=0.025
y(0.925)=1244.07, h=0.0125
y(0.9375)=1284.16, h=0.0125
y(0.95)=1326.08, h=0.0125
y(0.9625)=1369.91, h=0.0125
y(0.975)=1415.77, h=0.0125
y(0.9875)=1463.78, h=0.0125
y(1)=1514.04, h=0.0125
y(1.0125)=1566.7, h=0.0125
y(1.025)=1621.89, h=0.0125
y(1.0375)=1679.75, h=0.0125
y(1.05)=1740.44, h=0.0125
y(1.0625)=1804.13, h=0.0125
y(1.075)=1871, h=0.0125
y(1.0875)=1941.23, h=0.0125
y(1.1)=2015.04, h=0.0125
y(1.1125)=2092.63, h=0.0125
y(1.125)=2174.24, h=0.0125
y(1.1375)=2260.12, h=0.0125
y(1.15)=2350.54, h=0.0125
y(1.1625)=2445.79, h=0.0125
y(1.175)=2546.16, h=0.0125
y(1.1875)=2652, h=0.0125
y(1.2)=2763.65, h=0.0125
y(1.2125)=2881.49, h=0.0125
y(1.225)=3005.94, h=0.0125
y(1.2375)=3137.43, h=0.0125
y(1.25)=3276.43, h=0.0125
y(1.2625)=3423.46, h=0.0125
y(1.275)=3579.07, h=0.0125
y(1.2875)=3743.83, h=0.0125
y(1.3)=3918.41, h=0.0125
y(1.3125)=4103.47, h=0.0125
y(1.325)=4299.77, h=0.0125
y(1.3375)=4508.11, h=0.0125
y(1.35)=4729.35, h=0.00625
y(1.35625)=4845.11, h=0.00625
y(1.3625)=4964.45, h=0.00625
y(1.36875)=5087.5, h=0.00625
y(1.375)=5214.41, h=0.00625
y(1.38125)=5345.3, h=0.00625
y(1.3875)=5480.34, h=0.00625
y(1.39375)=5619.66, h=0.00625
y(1.4)=5763.44, h=0.00625
y(1.40625)=5911.83, h=0.00625
y(1.4125)=6065, h=0.00625
y(1.41875)=6223.14, h=0.00625
y(1.425)=6386.44, h=0.00625
y(1.43125)=6555.09, h=0.00625
y(1.4375)=6729.28, h=0.00625
y(1.44375)=6909.25, h=0.00625
y(1.45)=7095.2, h=0.00625
y(1.45625)=7287.36, h=0.00625
y(1.4625)=7485.99, h=0.00625
y(1.46875)=7691.33, h=0.00625
y(1.475)=7903.64, h=0.00625
y(1.48125)=8123.19, h=0.00625
y(1.4875)=8350.28, h=0.00625
y(1.49375)=8585.2, h=0.00625
y(1.5)=8828.27, h=0.00625
Приложение В. Листинг программы «Ilya RK-4 версия 1.43»
// ----------------------------------------------------------------------- //
#include <dos.h>
#include <stdio.h>
#include <conio.h>
#include <math.h>
#include <graphics.h>
#include <stdlib.h>
#define EPSILON 0.00001
#define MAXSTEP 1
#define VERSION 1.43
// ----------------------------------------------------------------------- //
double f(double x, double y);
double do_step(double h, double x_cur, double y_cur);
void title(void);
void main(void);
// ----------------------------------------------------------------------- //
double f(double x, double y)
{
// Правая часть ДУ f(x,y)
return (pow(2.718,x)*y);
}
// ----------------------------------------------------------------------- //
void main(void)
{
int i; // Вспомогательный счетчик
int metka; // Метка на осях
int flag = 0; // Флаг правого конца интегрирования
int metka1, metka2; // Переменные меток на осях координат
double err = 0; // Погрешность
double x0, y0; // Координаты точки начального условия
double big2_step_res, super_step_res; // Результаты длинных шагов
double k = 1; // Коэффициент коррекции
double zoom = 1; // Масштаб на графике
double big_step_res, small_step_res; // Результаты шагов интегрирования
double a, b; // Границы
double temp; // Переменная для служебных нужд
double x_cur, y_cur; // Переменные метода РК
double h; // Шаг интегрирования
double f_max = 0, f_min = 0; // Максимальное и минимальное значение кривой
double norma = 0; // Норма (для корректного масштабирования графика)int c = 8; // Переменная цвета разделительных линий
FILE *myfile; // Указатель на текстовый файл с таблицей значений
// Инициализируем графический адаптер
int gdriver = DETECT, gmode, errorcode;
initgraph(&gdriver, &gmode, "");
errorcode = graphresult();
if (errorcode != grOk)
{
printf("Ошибка инициализации графики: %s\n", grapherrormsg(errorcode));
getch();
}
textcolor(0);
setbkcolor(0);
title();
printf("y'=f(x,y), y(x0)=y(a)=y0, [a,b] - отрезок интегрирования\n");
label1: printf("\na=");
scanf("%lg", &a);
printf("b=");
scanf("%lg", &b);
// Авто смена границ при необходимости
if (a > b)
{
temp = a;
a = b;
b = temp;
}
if (a == b)
{
printf("Начало отрезка интегрирования совпадает с его концом, повторите ввод!\n");
goto label1;
}
printf("y(%lg)=", a);
scanf("%lg", &y0);
title();
printf("[%lg,%lg] - границы интегрирования, y(%lg)=%lg - начальное условие.\n", a, b, a, y0);
// Инициализация
h = fabs(b - a) / 10;
if (h > 0.1) h = 0.1;
x_cur = a;
y_cur = y0;
f_max = y_cur;
f_min = y_cur;
myfile = fopen("rk4.txt", "w");
fprintf(myfile, "Program: Ilya RK4 Version %g\n", VERSION);
fprintf(myfile, "Method: Runge-Kutta\n");
fprintf(myfile, "The order of method: 4\n");
fprintf(myfile, "Automatic integration step select: Enabled\n");
fprintf(myfile, "[a,b]=[%lg,%lg], y(%lg)=%lg\n", a, b, a, y0);
while (x_cur <= b)
{
if (flag > 1) break;
big_step_res = do_step(h, x_cur, y_cur);
temp = do_step(h / 2, x_cur, y_cur);
small_step_res = do_step(h / 2, x_cur + h / 2, temp);
err = fabs(big_step_res - small_step_res);
// Уменьшение длины шага
if (err > EPSILON)
{
h = h / 2;
continue;
}
// Увеличение длины шага
big2_step_res = do_step(h, x_cur + h, big_step_res);
super_step_res = do_step(2 * h, x_cur, y_cur);
if (fabs(big2_step_res - super_step_res) < EPSILON / 2)
{
h *= 2;
continue;
}
if (h > MAXSTEP) h = MAXSTEP;
// Защита от сбоев
if (h < pow(EPSILON, 2))
{
printf("Ошибка! Возможно, функция разрывна.\nПроинтегрировать на данном интервале невозможно. Скорее всего, g(%lg)=", x_cur);
fprintf(myfile, "Ошибка! Возможно, функция разрывна.\nПроинтегрировать на данном интервале невозможно. Скорее всего, g(%lg)=", x_cur);
if (y_cur < 0)
{
printf("-oo.\n");
fprintf(myfile, "-oo.\n");
}
else
{
printf("+oo.\n");
fprintf(myfile, "+oo.\n");
}
getch();
fclose(myfile);
exit(1);
}
printf("y(%lg)=%lg, err=%lg, h=%lg\n", x_cur, y_cur, err, h);
if (y_cur < f_min) f_min = y_cur;
if (y_cur > f_max) f_max = y_cur;
fprintf(myfile, "y(%lg)=%lg, h=%lg\n", x_cur, y_cur, h);
if (x_cur + h > b) h = fabs(b - x_cur);
x_cur += h;
y_cur = big_step_res;
if (x_cur >= b) flag++;
}
fclose(myfile);
printf("\nТаблица значений записана в файл rk4.txt.\n");
printf("\nНажмите любую клавишу для построения графика...");
flag = 0;
getch();
// Построение графика
cleardevice(); clrscr();
if (fabs(a) > fabs(b)) zoom = fabs(getmaxx() / 2 / a);
else zoom = fabs(getmaxx() / 2 / b);
// Рисуем границы
for (i = 0 ; i < getmaxy() ; i += 5)
{
if (c == 8) c = 0;
else c = 8;
setcolor(c);
line(a * zoom + getmaxx() / 2, i, a * zoom + getmaxx() / 2, i + 5);
line(b * zoom + getmaxx() / 2 - 1, i, b * zoom + getmaxx() / 2 - 1, i + 5);
}
if (fabs(f_min) > fabs(f_max)) norma = fabs(f_min) * zoom;
else norma = fabs(f_max) * zoom;
// Определение коэффициента коррекции
k = (getmaxy() / 2) / norma;
// Предотвращение чрезмерного масштабирования
if (k < 0.0001) k = 0.0001;
if (k > 10000) k = 10000;
for (i = 0 ; i < getmaxx() ; i += 5)
{
if (c == 8) c = 0;
else c = 8;
setcolor(c);
line(i, -y0 * zoom * k + getmaxy() / 2, i + 5, -y0 * zoom * k + getmaxy() / 2);
line(i, -f_min * zoom * k + getmaxy() / 2, i + 5, -f_min * zoom * k + getmaxy() / 2);
line(i, -f_max * zoom * k + getmaxy() / 2, i + 5, -f_max * zoom * k + getmaxy() / 2);
}
metka = ceil((-y0 * zoom * k + getmaxy() / 2) / 16);
if (metka <= 0) metka = 1;
if (metka == 15) metka = 16;
if (metka > 25) metka = 25;
gotoxy(1, metka);
printf("Y=%.2g", y0, metka);
metka = ceil((-f_max * zoom * k + getmaxy() / 2) / 16);
if (metka <= 0) metka = 1;
if (metka == 15) metka = 16;
if (metka > 25) metka = 25;
gotoxy(1, metka);
printf("Y=%.2lg", f_max, metka);
metka = ceil((-f_min * zoom * k + getmaxy() / 2) / 16);
if (metka <= 0) metka = 1;
if (metka == 15) metka = 16;
if (metka > 25) metka = 25;
gotoxy(1, metka);
printf("Y=%.2lg", f_min, metka);
// Пишем границы, делаем отметки на осях координат
metka1 = ceil((a * zoom + getmaxx() / 2) / 8);
if (metka1 < 1) metka1 = 1;
if (metka1 > 75) metka1 = 75;
if (metka == 17) metka = 18;
gotoxy(metka1, 15);
if (a != 0) printf("%.2lg", a);
metka2 = ceil((b * zoom + getmaxx() / 2 - 1) / 8);
if (metka2 - metka1 < 7) metka2 = metka1 + 7;
if (metka2 < 1) metka2 = 1;
if (metka2 > 75) metka2 = 75;
gotoxy(metka2, 15);
printf("%.2lg", b);
gotoxy(80, 17);
printf("X");
gotoxy(42,1);
printf("Y");
gotoxy(39, 15);
printf("0");
// Рисуем систему координат
setcolor(15);
line(0, getmaxy() / 2, getmaxx(), getmaxy() / 2);
line(getmaxx() / 2, 0, getmaxx() / 2, getmaxy());
line(getmaxx() / 2, 0, getmaxx() / 2 - 5, 10);
line(getmaxx() / 2, 0, getmaxx() / 2 + 5, 10);
line(getmaxx(), getmaxy() / 2, getmaxx() - 10, getmaxy() / 2 + 5);
line(getmaxx(), getmaxy() / 2, getmaxx() - 10, getmaxy() / 2 - 5);
setcolor(10);
h = fabs(b - a) / 10;
if (h > 0.1) h = 0.1;
y_cur = y0;
x_cur = a;
f_max = y_cur;
f_min = y_cur;
x0 = zoom * a + getmaxx() / 2;
y0 = (zoom * (-y_cur)) * k + getmaxy() / 2;
while (x_cur <= b)
{
if (flag > 1) break;
big_step_res = do_step(h, x_cur, y_cur);
temp = do_step(h / 2, x_cur, y_cur);
small_step_res = do_step(h / 2, x_cur + h / 2, temp);
err = fabs(big_step_res - small_step_res);
if (err > EPSILON)
{
h = h / 2;
continue;
}
big2_step_res = do_step(h, x_cur + h, big_step_res);
super_step_res = do_step(2 * h, x_cur, y_cur);
if (fabs(big2_step_res - super_step_res) < EPSILON / 2)
{
h *= 2;
continue;
}
if (h > MAXSTEP) h = MAXSTEP;
line (x0, y0, zoom * x_cur + getmaxx() / 2, zoom * (-y_cur) * k + getmaxy() / 2);
x0 = zoom * (x_cur) + getmaxx() / 2;
y0 = (zoom * (-y_cur)) * k + getmaxy() / 2;
if (x_cur + h > b) h = fabs(b - x_cur);
x_cur += h;
y_cur = big_step_res;
if (x_cur >= b) flag++;
}
while (getch() != 0);
}
// ----------------------------------------------------------------------- //
void title(void)
{
// Печать заголовка программы
cleardevice(); clrscr();
printf(" Решение дифференциальных уравнений методом Рунге-Кутты 4-го порядка\n");
printf(" с автоматическим выбором длины шага\n");
printf(" Разработал Щербаков Илья, гр. 520212, версия %g\n", VERSION);
printf("____________________________________________________\n");
}
// ----------------------------------------------------------------------- //
double do_step(double h, double x_cur, double y_cur)
{
double k1, k2, k3, k4, delta_y_cur;
k1 = f(x_cur, y_cur);
k2 = f(x_cur + (h / 2), y_cur + (h / 2) * k1);
k3 = f(x_cur + (h / 2), y_cur + (h / 2) * k2);
k4 = f(x_cur + h, y_cur + h * k3);
delta_y_cur = (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4);
return(y_cur + delta_y_cur);
}
// ----------------------------------------------------------------------- //
[1] Дж. Холл, Дж. Уатт «Современные численные методы решения обыкновенных дифференциальных уравнений», М., Мир, 1979, стр. 77.
[2] «Между тем еще нет доказательства, что эти приближенные методы сходятся, или, что практически важнее, нет критерия, определяющего, сколь малым надо сделать шаги, чтобы достичь предписанной точности» – так писал Рунге в 1905 году.
[3] Хайрер Э., Нёрсетт С., Ваннер Г. «Решение обыкновенных дифференциальных уравнений. Нежесткие задачи», М., Мир, 1990, стр. 169.
[4] Амоносов А.А., Дубинский Ю.А., Копченова Н.В. «Вычислительные методы для инженеров», М., Высшая школа, 1994, стр. 445.
[5] Тестирование проводилось на компьютере на базе процессора Intel Pentium 4B. На компьютерах, оснащенных другими процессорами, время выполнения первого и второго этапов может быть другим.
Похожие работы
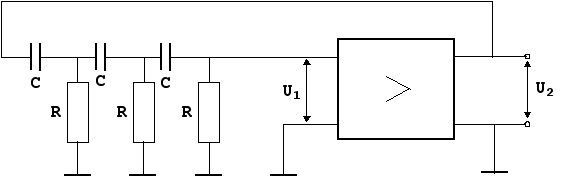
... 1 0.0001 Графики решения приведены на Рисунке 8, а численные значения в таблице 8. Рисунок показывает, что выходное напряжение автогенератора (кривая 1) достаточно близко к синусоидальному, чего нельзя сказать о входном напряжении усилителя (кривая 2). Таблица 8 АРГУМЕНТ ФУНКЦИЯ 1 ФУНКЦИЯ 2 ФУНКЦИЯ 3 ФУНКЦИЯ 4 ФУНКЦИЯ 5 370.0 ...
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
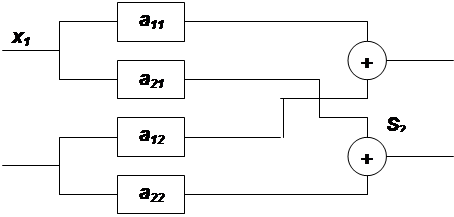
... методы (метод Гаусса). Однако, при решении на ЭВМ систем высокого порядка (более 200 уравнений в системе), предпочтительными являются итерационные методы. Реализация решения задачи анализа линейного стационарного объекта может быть осуществлена с помощью средств матричной алгебры пакета MathCAD. 1.2. Последовательность выполнения работы 1. Согласно номеру варианта (две последние цифры ...

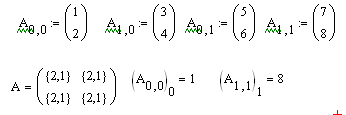


0 комментариев