Навигация
F(u)=u×(u + sin(u) – 3)×exp(cos(u))
2. f(u)=u×(u + sin(u) – 3)×exp(cos(u))
dicho(f, 1, 3, 0.0001) = 2.18f(2.18)=0
Задача 16. Пусть функция f(x) вещественной переменной x непрерывна на отрезке [a, b]. Составить программу нахождения на [a, b] любого вещественного корня f(x). При отсутствии корней, должно быть выдано значение ¥ (10307).
Решение. Отличие постановки этой задачи от предыдущей в том, что здесь априори ничего неизвестно о знаках функции на концах отрезка и, следовательно, корней f(x) уже может и не быть. Однако метод дихотомии с успехом может быть применен и в данном случае. Соответствующий алгоритм может быть записан так.

Контрольные примеры.
Рассмотрим функции примеров из предыдущей задачи. Имеем:
dichot(y,1,7,0.001)=10307 , dichot(f,2.17,3,0.0001)=2.18 .
Периодическое продолжение
Задача 17. Составить программу, которая для функции g(x), определенной при x Î [a,b), строит функцию peri(g,a,b,x), являющуюся периодическим продолжением g(x) на всю действительную ось c периодом w = b – a.
Решение. Нам, очевидно, требуется определить функцию следующего вида.
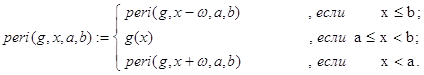
На языке Mathcad это будет выглядеть практически так же:
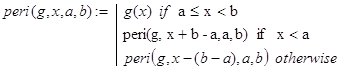
Заметим, что при x находящемся вдали от промежутка [a,b) вычисления значения функции peri() требует значительного количества рекурсивных вызовов. Происходит это по той причине, что за один такой вызов мы продвигаемся в направлении [a,b) лишь на расстояние w=b-a.
Значительно эффективней проводятся вычисления по функции F(g,x,a,b) также являющейся периодическим продолжением g(x) на всю числовую ось.
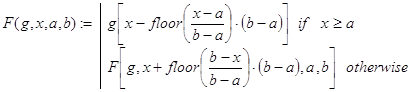
Контрольные примеры.
1. Пусть y(x) = x2×sin(x). Тогда:
peri(y,1,0,2) = 0.841 peri(y,3,0,2) = 0.841
peri(y,-1,0,2) = 0.841 peri(y,1001,0,2)=0.841
2. На рис. 3.4 изображен график функции H(t), являющейся периодическим продолжением функции y(x)= x2×sin(x) для x Î [-10, 0). H(t) построено с помощью программы-функции F(), а график выведен на промежутке [-10,20) с шагом h=0.1.
t:= -10,-9.9..20 H(t):=perri(y,t,-10,0)
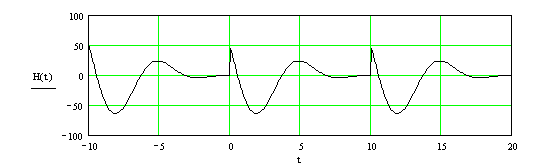
Рис. 3.4 Периодическое продолжение функции y(x)= x2×sin(x)
для x Î [-10, 0).
3.14 Функция Аккермана
Задача 18. Пусть n и m целые неотрицательные числа. Написать программу, вычисляющую классическую в теории рекурсии функцию Аккермана:
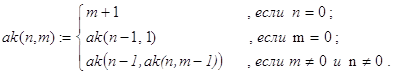 (5)
(5)
Решение. Вычислить функцию Аккермана, исходя непосредственно из определения (5), удается лишь для некоторых малых n и m. Связано это со сложностью и необычностью рекурсивного определения. В общем случае не только ak() вычисляется через ak(), но и второй из аргументов функции также требует рекурсивного вызова ak(). Соответствующая программа-функция может быть записана так:
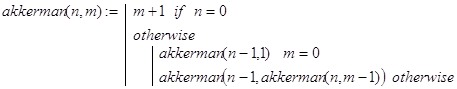
Контрольные примеры.
![]()
Следующий вариант программы для вычисления функции Аккермана включает в себя лишь один рекурсивный вызов:
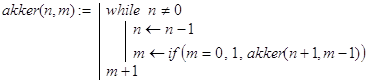
Замечание. Для m=0..4 справедливы соотношения [5, с. 69]:
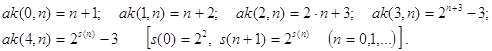
Эти формулы могут оказаться полезными при построении контрольных примеров для отладки новых более эффективных вариантов программ вычисления функции Аккермана.
В работе [5, c. 256-260] приведен нерекурсивный вариант алгоритма вычисления значений функции Аккермана.
3.15 Функция Маккарти
Задача 19. Функция Маккарти. Показать, что для приведенной ниже рекурсивной программы-функции
![]()
при целочисленных значениях n справедлива формула:
![]() (6)
(6)
Решение. Относительно параметра n возможны три случая:
n > 100,90£ n £100, -¥ < n<90.
В первом из них в силу базы рекурсии следует, что makkarti(n)=n-10. Во втором случае:
![]()
Наконец, всякое начальное n<90 в соответствии с декомпозицией через конечное число рекурсивных вызовов приводит ко второму случаю. Отсюда опять makkarti(n)=91. Таким образом (6) справедливо во всех случаях.
Заметим, что из проведенных рассуждений вытекает, что рассматриваемая функция может быть определена более просто, например, так:
![]()
Задача 20. Показать, что для приведенной ниже рекурсивной программы-функции
![]()
при целочисленных значениях x справедлива формула:
![]() (7)
(7)
Решение. При y=0 и z=1 имеем z=y!. Далее из характера декомпозиции функции cadiou() ясно, что z=y! остается инвариантом в ходе рекурсивных вызовов. Вместе с условием завершения x=y это и дает z=x! и (7) установлено.
3.17 Количество делителей
Задача 21. Количество делителей. Составить программу-функцию подсчета для натурального числа n количества всех его делителей.
Решение. Перейдем к более общей задаче. Подсчитаем для натурального числа n количества всех его делителей, меньших или равных заданному натуральному числу x. Пусть dn(n) и dnx(n,x) - соответственно функции для решения исходной и обобщенной задач. Очевидно, что dn(n)=dnx(n,n).
Рекурсивную функцию dnx(n,x), по которой последовательно подвергаются испытанию на делители n все числа от 1 до x включительно, можно определить так:
![]()
![]()
Контрольные примеры.
![]()
Далее, если n ³2 и dn(n)=2, то число n – простое. Однако проверка n на простоту этим способом весьма неэкономна.
3.18 Простые числа
Задача 22. Составить программу-функцию проверяющую, является ли заданное натурально число n простым?
Решение. Пусть рекурсивная функция isprim(n) является решением задачи и
![]()
Дальнейшие рассуждения являются иллюстрацией использования классического приема “вложения” (Дж. Маккарти, 1962). Перейдем к рассмотрению следующей обобщенной задачи. Пусть a, b, n - натуральные числа и 2£a£b£n. Верно ли, что заданное n не делится ни на одно целое из отрезка [a, b]? Пусть эту задачу решает функция
![]()
Ниже приведено три рекурсивных варианта реализации этой функции. По первому из них проверке на делитель n последовательно подвергаются числа: a, a+1, … , b; по второму - эти же числа в обратном порядке и, наконец, по третьему - a, b, a+1, b-1, … .
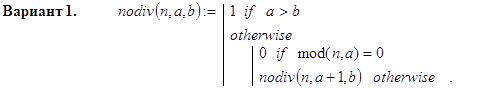

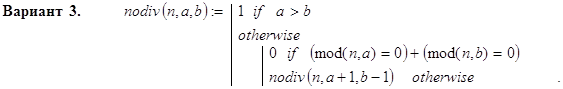
Контрольные примеры.
![]()
Далее, натуральное число n³2 является простым, если оно не имеет делителей на отрезке ![]() , поэтому характеристическая функция isprim(n) через функцию nodiv(n,a,b) может быть выражена так:
, поэтому характеристическая функция isprim(n) через функцию nodiv(n,a,b) может быть выражена так:
![]()
Контрольные примеры.
![]()
Задача 23. Составить программу-функцию pi(x), которая подсчитывает количество простых чисел, не превосходящих заданное число x.
Решение. С помощью функций nodiv() или isprim() рекурсивный вариант функции pi(x) строится достаточно просто, исходя из такого декомпозиционного утверждения. Количество простых чисел, не превосходящих x, составляется из количества простых чисел меньших или равных x-1 плюс значение функции isprim(x). Поэтому:
![]()
Контрольные примеры.
![]()
Задача 24. Составить программу pn(n), которая вычисляет n-ое простое число (n – натуральное).
Решение. Предварительно напишем рекурсивную подпрограмму-функ-цию minp(m) нахождения наименьшего простого числа, большего или равного m (m – натуральное число). Сделать это можно, например, так:
![]()
Контрольные примеры.
![]()
Тогда искомая функция pn(n) может быть определена так:
![]()
Контрольные примеры.
![]()
Задача 25. Составить программу-функцию вычисления значений многочлена по схеме Горнера.
Решение. Пусть f(x) многочлен с вещественными или комплексными коэффициентами и v – вектор этих коэффициентов:
![]() (8)
(8)
![]() (9)
(9)
Вычисление f(x) в точке x по схеме Горнера проводится от самых внутренних скобок и далее в соответствии с представлением:
![]()
Отсюда ясно, как записать рекурсивный и не рекурсивный варианты алгоритмов вычисления f(x). Нас интересует только первый из них. Параметрами задачи можно считать вектор v и точку a для вычисления f(a). Тривиальный случай – многочлен нулевой степени: f(a) = a0. Декомпозиция получается из указанной выше расстановки скобок в записи f(x). Соответствующая программа-функция выглядит, например, так.
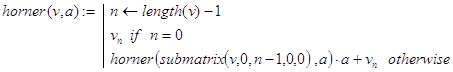
Контрольные примеры.
![]()
Замечание. Параметр n – это константа, равная степени многочлена. По вектору v она определяется однозначно. Однако в каждом рекурсивном вызове проводится перевычисление n. Избежать лишней вычислительной работы в подобных ситуациях можно двумя способами. Или определять такие константы заранее вне текста программы-функции или передавать их значения через дополнительные аргументы функции.
3.20 Деление многочлена на двучленЗадача 26. Составить программу-функцию, по которой для многочлена (8) с коэффициентами, составляющими вектор (9) и двучлена x-x0 (x0 - вещественное или комплексное число), вычисляется вектор c:
![]()
такой, что
![]()
и
![]()
Решение. Если в соотношении, связывающем многочлены f(x) и q(x), осуществить приведение к общему знаменателю и приравнивание коэффициентов при одинаковых степенях x, то для определения компонент вектора c получим следующую систему линейных уравнений.
![]()
Отсюда вытекает, что c = qu(v,x0), где рекурсивное определение функции qu() может выглядеть, например, так.
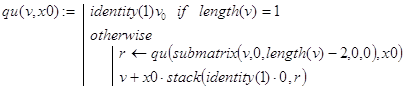
Контрольный пример.
![]()
Иными словами:
![]()
Задача 27. Пусть коэффициенты многочленов fn(x) и gm(x) заданы компонентами векторов v и w:
![]() (10)
(10)
![]() (11)
(11)
Составить рекурсивную программу-функцию вычисляющую коэффициенты многочлена hn+m(x)=fn(x)×gm(x) и возвращающую их в виде компонентов вектора:
![]()
Решение. Поскольку
![]()
где
![]()
то вполне можно организовать рекурсию по параметру m - степени второго сомножителя. И в качестве решения может быть предложена следующая функция:
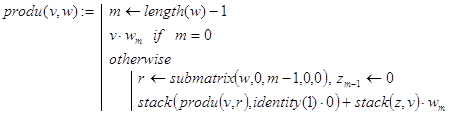
Ясно, что аналогично можно было бы реализовать рекурсию и по параметру n - степени первого сомножителя. В любом случае величины m и n определяют количество рекурсивных обращений. Поэтому в данной задаче рекурсию выгодно реализовывать по параметру со значением, равным min(n,m).
Контрольный пример.
![]()
![]()
3.22 Произведение биномов
Задача 28. Составить программу-функцию возвращающую коэффициенты многочлена g(x), который получается в результате перемножения биномов (x-vk): (k=0,1,…n-1; n³1): ![]()
Решение. Будем считать, что свободные члены биномов заданы в виде компонентов некоторого вектора v: ![]() а результат вычислений должен возвращаться также в виде вектора. Поскольку
а результат вычислений должен возвращаться также в виде вектора. Поскольку
![]()
то несложно организовать рекурсию по количеству перемножаемых биномов. Соответствующая программа функция могла бы выглядеть так:

Контрольный пример.
![]()
3.23 Деление многочлена на многочлен
Задача 29. Пусть выполнены соотношения (10)-(11), то есть многочлены fn(x) и gm(x) степеней n и m (n,m³0) соответственно заданы своими коэффициентами в виде компонентов векторов v и w. Пусть, далее, при m=0, то есть если gm(x) есть константа, gm(x)¹0. Составить программу-функцию нахождения частного q(x) и остатка r(x) при делении fn(x) на gm(x):
fn(x)=q(x)×gm(x)+r(x), (12)
где степень r(x) меньше m (при m=0 r(x)º0).
Решение. Представление (12) единственно. В дальнейшем нам удобно считать, что степень r(x) равна m-1 с возможно нулевыми коэффициентами при старших степенях x.
При m=0 решение задачи очевидно:
q(x)=fn(x)/w0,r(x)=0. (13)
Далее, при n<=m имеем
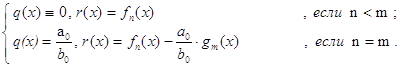 (14)
(14)
Пусть n>m и q1(x) и r1(x) - частное и остаток от деления (fn(x)-an-1)/x на gm(x):
![]()
Из этого соотношения вытекает, что
![]()
Вместе с (12) это дает:
 (15)
(15)
Если соотношения (13)-(14) рассматривать в качестве базы рекурсии, то равенства (15) определяют декомпозицию. Считаем, что в результате вычислений должен быть сформирован и возвращен составной вектор qr=[q r]T, где q и r соответственно векторы коэффициентов многочленов q(x) и r(x). Соответствующая программа-функция, реализующая эти идеи, выглядит так:
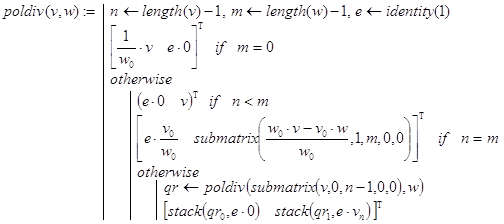
Контрольные примеры.
![]()
![]()
![]()
![]()
Замечание. Функция poldiv() возвращает составной вектор [q r]T , в котором второй компонент-вектор r может содержать “ведущие” нули. При необходимости эти нули можно погасить, то есть выделить из r подвектор, начинающийся с первого из ненулевых компонент r. Сделать это можно, например, с помощью приведенной ниже рекурсивной функции nulera(u). Если все компоненты u равны нулю, то nulera(u) возвращает 0.
![]()
3.24 Разбиение целого на части
Задача 30. Составить программу-функцию подсчета количества x(m) разбиений натурального числа m, то есть его представления в виде суммы натуральных чисел.
Решение. Пусть, например, m=6. Тогда разбиениями m являются его представления в виде:
6;
5+1;
4+2, 4+1+1;
3+3, 3+2+1, 3+1+1+1;
2+2+2, 2+2+1+1, 2+1+1+1+1;
1+1+1+1+1+1;
Таким образом, x(m)=11 и понятно, что простым перебором возможных случаев уже при m>10 справиться с задачей достаточно сложно.
Для решения исходной задачи перейдем к рассмотрению обобщенной задачи. Составить программу-функцию подсчета количества P(m,n) разбиений натурального числа m со слагаемыми, не превосходящими n. Ясно, что x(m)=P(m,m). Поэтому, достаточно научиться вычислять значения функции P(m,n). Но для неё нетрудно выделить рекурсивную базу и указать правило декомпозиции. Сделать это можно исходя из следующих вполне прозрачных свойств этой функции.
1. P(m,1)=1 - существует только одно разбиение m, в котором слагаемые не превосходят единицы, а именно: m=1+1+…+1.
2. P(1,n)=1 - число единица имеет только одно представление при любом n.
3. P(m,n)=P(m,m) при n>m - слагаемые, большие m в разбиениях отсутствуют.
4. P(m,m)=P(m,m-1)+1 - существует лишь одно разбиение со слагаемым равным m. Все иные разбиения имеют слагаемые не превосходящие m-1.
5. P(m,n)=P(m,n-1)+P(m-n,n) (n<m). Обоснование этого соотношения проводится так. Все разбиения m на сумму слагаемых, не превосходящих n можно разбить на два непересекающихся класса: суммы, не содержащие n в качестве слагаемого и суммы, содержащие такое n. Количество элементов первого класса равно P(m,n-1), а количество элементов второго класса подсчитаем так. Без учета слагаемого n суммы элементов второго класса равны m-n. Значит их общее количество равно P(m-n,n) и, следовательно, общее количество элементов второго класса также равно этой величине. Тем самым свойство 5 установлено.
Первые два свойства определяют базу рекурсии, а три следующие задают декомпозицию. Строго в соответствии с этими утверждениями и составлена рекурсивная программа-функция deco(n,m) для вычисления величины P(m,n).
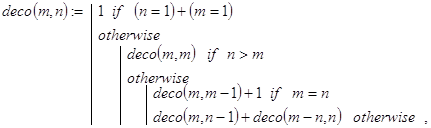
![]()
Контрольные примеры.
![]()
3.25 Максимальный и минимальный элементы
Пусть одномерный массив задан вектором ![]() Часто возникает задача поиска максимального (минимального) элемента v. Вне зависимости от того, идет ли речь о нахождении максимального по значению элемента или его позиции в v, поиск можно реализовать за один просмотр массива. Правда в последнем случае решение может оказаться неоднозначными и постановка задачи требует уточнения. Например, отыскивается позиция максимального элемента с наименьшим индексом. В любом случае сравнение характеристик различных алгоритмов поиска проводят по количеству тех или иных выполняемых ими операций. Чаще всего это операции сравнения.
Часто возникает задача поиска максимального (минимального) элемента v. Вне зависимости от того, идет ли речь о нахождении максимального по значению элемента или его позиции в v, поиск можно реализовать за один просмотр массива. Правда в последнем случае решение может оказаться неоднозначными и постановка задачи требует уточнения. Например, отыскивается позиция максимального элемента с наименьшим индексом. В любом случае сравнение характеристик различных алгоритмов поиска проводят по количеству тех или иных выполняемых ими операций. Чаще всего это операции сравнения.
Рекурсивная функция maxv(v) находит максимальный элемент v ровно за n-1 операцию сравнения. Декомпозиция реализуется по длине вектора и опирается на такое утверждение. Решить исходную задачу для v - это то же самое, что решить её для подвектора, получаемого из v удалением его первого компонента, сравнить полученное значение с удаленным элементом и, наконец, выбрать не меньшее из них.
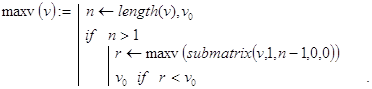
Контрольные примеры.
![]()
Замечание. При подсчете количества операций сравнения элементов массива не учитываются сравнения с управляющими переменными рекурсии или цикла. Это же самое касается и других программ, приведенных ниже.
Аналогично строится и функция minv(v) - нахождения за n-1 операцию сравнения минимального по значению элемента массива. Нетрудно написать рекурсивную функцию одновременного поиска минимального и максимального значений v за 2×n-2 операции сравнения. Выглядеть она может, например, так:
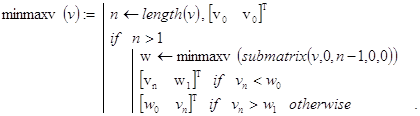
Контрольные примеры.
![]()
Однако одновременное нахождение максимального и минимального значений v может быть реализовано гораздо эффективней. Соответствующий результат зафиксирован в следующей задаче.
Задача 31. Написать рекурсивную программу-функцию, находящую одновременно максимальный и минимальный элементы массива v за ![]() операций сравнения.
операций сравнения.
Решение. Если длина вектора v равна единице, то решением задачи можно считать вектор ![]() При длине вектора v, равной двум, решение находится за одно сравнение. Пусть длина вектора больше двух. Тогда из двух первых компонентов непосредственно найдем наибольшее и наименьшее (одно сравнение), решим исходную задачу для подвектора, получающегося из v удалением этих компонентов и, наконец, осуществим правку полученного решения для подвектора за счет первых двух компонентов (два сравнения). Именно эти идеи и реализуются рекурсивной функцией minmax():
При длине вектора v, равной двум, решение находится за одно сравнение. Пусть длина вектора больше двух. Тогда из двух первых компонентов непосредственно найдем наибольшее и наименьшее (одно сравнение), решим исходную задачу для подвектора, получающегося из v удалением этих компонентов и, наконец, осуществим правку полученного решения для подвектора за счет первых двух компонентов (два сравнения). Именно эти идеи и реализуются рекурсивной функцией minmax():
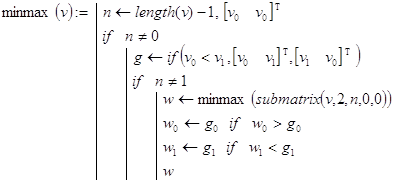
Контрольный пример.
![]()
Подсчитаем теперь S - общее количество сравнений:
![]()
![]()
Тем самым решение задачи завершено полностью.
В следующем варианте minmax() - функции minmax1() используются три вспомогательных параметра: a, b, i. Первые два из них служат для фиксации текущих значений минимального и максимального элементов массива, а последний - для нумерации рекурсивных обращений. Как и в предыдущем случае, каждый рекурсивный вызов уменьшает обрабатываемый массив на два элемента. Но здесь, в отличие от minmax(), они удаляются с разных его концов. Использование вспомогательной функции mima(v) избавляет нас от сложного обращения к minmax1().
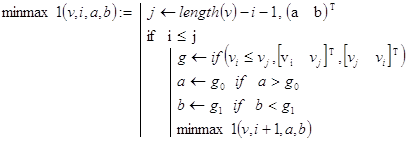
![]()
Контрольный пример.
![]()
Задача 32. Написать рекурсивную программу-функцию, находящую одновременно позиции максимального и минимального элементов массива v за ![]() операций сравнения.
операций сравнения.
Решение. Для решения данной задачи можно использовать тот же самый алгоритм, который реализуется функцией minmax1(), подвергая запоминанию не текущие значения минимального и максимального элементов массива, а их индексы. Соответствующие функции posmima() и pmima() можно записать так:
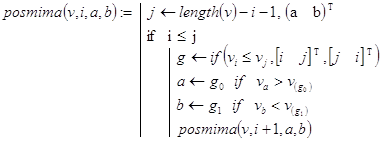
![]()
Контрольный пример.
![]()
Замечание. Рекурсивная функция posmima() позволяет реализовать сортировку массива v по такому алгоритму:
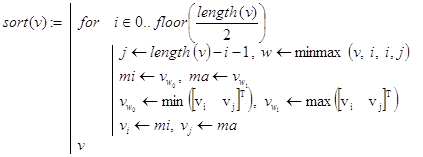
Контрольные примеры.
![]()
![]()
Задача 33. Последовательность из латинских букв строится следующим образом. На нулевом шаге она пуста. На каждом последующем шаге последовательность удваивается, то есть приписывается сама к себе, и к ней слева добавляется очередная буква алфавита (a,b,c,…). По заданному числу n определить символ, который стоит на n-ом месте последовательности, получившейся после шага 26.
Решение. Эта задача предлагалась участникам областных туров Всероссийской олимпиады школьников по информатике в 1998 году. Приведем первые шаги формирования последовательности: 0 - пустая последовательность, 1 - a, 2 - baa,3 - cbaabaa, 4 - dcbaabaacbaabaa, … . Мы имеем явно рекурсивный процесс.
Построим более общую программу-функцию, чем это требуется по условиям задачи. Пусть abra(k,n) - n-ая буква в последовательности, полученной на шаге k (k=1..26). Тогда ясно, что abra(k,1) равно k-ой букве латинского алфавита. Этот факт можно взять в качестве базы рекурсии, а функцию для определения этой буквы записать так:
![]()
Декомпозицию удобно организовать по k, проводя “раскрутку” последовательности по шагам в обратном направлении. Это приводит к следующей функции:
![]()
Контрольные примеры.
![]()
Задача 34. Вложенные квадраты. Пусть на плоскости первый квадрат задан точками: M1(-1,-1), M2(-1,1), M3(1,1), M4(1,-1). Второй квадрат строится так, что вершины первого квадрата являются серединами его сторон и т.д. Составить рекурсивную программу-функцию, которая по заданному натуральному n строит систему из 2×n вложенных друг в друга описанным образом квадратов, точнее создает массив точек, последовательное соединение которых на плоскости отрезками и формирует эту систему (см. рис. 3.5).
Решение. Если учесть тот факт, что по условию задачи всегда строится четное число вложенных квадратов, то последовательность точек для построения первых двух из них можно задать непосредственно и считать соответствующую матрицу beg базой рекурсии:
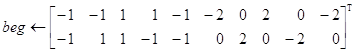
Обратите внимание, что в beg каждый из квадратов задается не четырьмя, а пятью точками. При этом первая и последняя из них совпадают. Это поможет впоследствии правильной прорисовке квадратов.
Далее, декомпозиция определяется таким утверждением. Если уже построена матрица ma точек для 2×(n-1) вложенных квадратов, то, пополнив её точками матрицы ![]() , получим матрицу точек для 2×n таких квадратов. Соответствующая рекурсивная функция, базирующаяся на этих фактах, может выглядеть так:
, получим матрицу точек для 2×n таких квадратов. Соответствующая рекурсивная функция, базирующаяся на этих фактах, может выглядеть так:
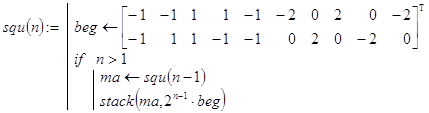
Контрольный пример. ![]() Результат вычислений представлен на рис. 3.5 c неодинаковым масштабом по осям.
Результат вычислений представлен на рис. 3.5 c неодинаковым масштабом по осям.
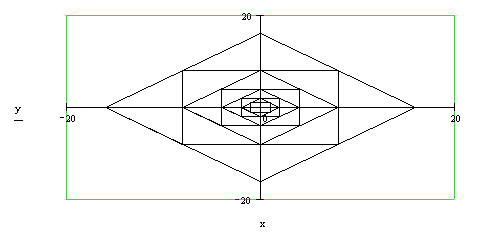
Рис. 3.5. Вложенные 2×n квадратов (n=4)
Задача 35. Вложенные многоугольники. Пусть на плоскости задан правильный n-угольник, вписанный в единичную окружность одна из вершин которого имеет координаты (cos(a), sin(a)), где a - некоторый угол. Второй правильный n-угольник строится так, что его вершины являются серединами сторон первого многоугольника и т.д. Составить рекурсивную программу-функцию, которая по заданному натуральному n строит систему из n вложенных друг в друга описанным образом многоугольников, точнее создает массив точек, последовательное соединение которых на плоскости отрезками и формирует эту систему (см. рис. 3.6).
Решение. Это задача в каком-то смысле является обобщением предыдущей. Здесь выводятся правильные вписанные n-угольники, количество их не обязательно четно и первая из вершин начального n-угольника может лежать в любой точке единичной окружности. Правда, здесь многоугольники не “описываются” один вокруг другого, а “вписываются” друг в друга. Но существа дела это не меняет.
Прежде всего, составим программу, которая формирует массив вершин правильного n-угольника, вписанного в окружность радиуса r и содержащего вершину (r×cos(a) r×sin(a)). Сделать это можно, например, так:
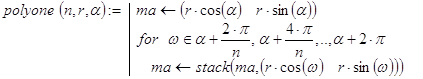
Тогда массив polyone(n,1,a) может служить базой рекурсии. Более того, эта функция при правильном выборе r и a позволяет получить массив вершин любого из следующих вписанных n-угольников, что помогает организовать и декомпозицию. Если уже построена матрица ma точек для (n-1)-го вписанного правильного n-угольника, то, пополнив её точками матрицы:
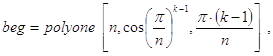
получим матрицу точек для 2×n таких многоугольников. Соответствующая рекурсивная функция, реализующая эти идеи, может выглядеть так:
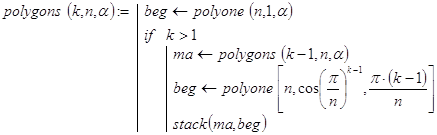
Контрольный пример. ![]() Результат вычислений представлен на рис. 3.6 c неодинаковым масштабом по осям.
Результат вычислений представлен на рис. 3.6 c неодинаковым масштабом по осям.

Рис. 3.6. k вложенных правильных n-угольников (k=20, n=6)
Несколько слов перед формулировкой новой задачи. В основах анализа [8, с. 17-38] операции сложения и умножения над натуральными числами определяются рекурсивным способом, опираясь на аксиомы Пеано “о существовании последующего числа” и “индукции”. Первая из названных аксиом звучит так: “для каждого натурального x имеется и притом только одно натуральное число, называемое его последующим и обозначаемое число x¢ ”.Постараемся промоделировать указанные выше и некоторые иные операции.
Моделирование арифметических операций
Задача 36. Для целых неотрицательных чисел n, m разрешены операции:
нахождения последующего числа (n+1) и предыдущего числа n-1 (n>0). Промоделировать с помощью рекурсивных функций операции нахождения суммы (n+m), разности (n-m (n³m)), умножения (n×m), возведения в степень nm (n>0), частного и остатка при делении n на m (n/m).
Решение.
A. Сумма: a+b. Очевидное соотношение
![]()
задает одновременно и базу рекурсии и правило декомпозиции. По нему и построена следующая рекурсивная программа-функция:
![]()
Контрольный пример: ![]()
B. Разность: a-b (a³b). В данном случае база рекурсии и декомпозиция могут быть извлечены из соотношения:
![]()
Соответствующая рекурсивная программа-функция выглядит так.
![]()
Контрольный пример: ![]()
C. Умножение: a×b. Будем считать, что операция сложения уже определена. Тогда соотношение, из которого легко извлекаются база и декомпозиция для данного случая выглядит следующим образом:
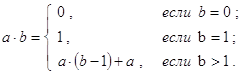
Соответствующая рекурсивная программа-функция может быть записана, например, так:
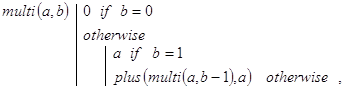
Контрольный пример: ![]()
D. Возведение в степень: ab (a¹0). Будем считать, что операция умножения уже определена. Тогда:
![]()
и рекурсивная программа-функция возведения в степень может быть задана так:
![]()
Контрольный пример: ![]()
E. Частное и остаток: a/b (b>0). В данной задаче речь идет об отыскании величин q и r из представления: a=q×b+r (0£r<b, q³0). Будем предполагать, что операция вычитания уже определена, а ответ должен быть возвращен в виде вектора с двумя компонентами: (q r)T. Если a<b, то q=0 и r=a. Этот факт и определяет базу рекурсии. Если же b>a, то a/b=1+(a-b)/b, что позволяет организовать декомпозицию. Все сказанное учтено в рекурсивной функции divi(q,a,b). В ней первый аргумент q является вспомогательным параметром. При обращениях к divi() он должен определять базовое значение частного, то есть быть равен нулю. Однако проще решать задачу с помощью вспомогательной функции div(a,b), возлагая на неё решение вопроса о правильном значении вспомогательного параметра вызовах divi(). Это довольно типичный случай при обобщениях исходной задачи за счет введения дополнительных параметров.
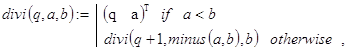
![]()
Контрольный пример. ![]()
Замечание. Моделирование различных операций возможно не только для целых неотрицательных чисел. Их можно было бы определить и для множества всех целых чисел и даже для множества вещественных чисел. Ограничимся рассмотрением одного примера. Напишем рекурсивную программу-функцию нахождения дробной части вещественного числа, если разрешены лишь операции x+1 и x-1. Вот один из возможных достаточно ясных вариантов её определения:
![]()
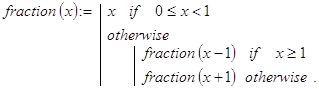
Контрольный пример. ![]()
Синтаксические языковые конструкции
Задача 37. Составить программу-функцию проверяющую, является ли данная последовательность символов идентификатором языка Фортран.
Решение. Будем считать, что речь идет о версиях Фортрана, где идентификатор определялся как последовательность из шести заглавных латинских букв и (или) цифр, начинающаяся с буквы и для символов была принята ASCII кодировка. Превратить последовательность символов в вектор соответствующих им ASCII-кодов можно с помощью встроенной функции str2vec(). Например:
![]()
Дополнительное ограничение на первый символ идентификатора (буква, но не цифра) усложняет общую проверку (или буква, или цифра). Чтобы действия были стандартными для всех символов, проверку первого из них будем осуществлять на допустимость отдельно в головной программе. Естественно там же располагать и проверку длины слова, которая должна находиться в пределах от 1 до 6. Тогда в подпрограмме останется решить вполне рекурсивную подзадачу: “если первый символ исходного слова не буква и не цифра, то формируем ответ “не идентификатор”. В противном случае, если длина слова равна единице, то возвращаем ответ “идентификатор”, а иначе укорачиваем слово на первый символ и снова решаем эту же подзадачу. Все сказанное и реализуется головной программой identity(word) и рекурсивной подпрограммой iden(v):
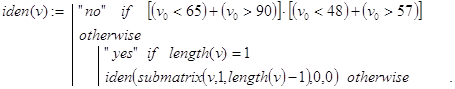
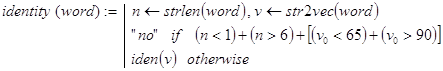
Контрольные примеры.
![]()
Замечание. В любом языке программирования все базовые языковые конструкции (идентификаторы, константы, переменные, выражения, метки, типы и т.п.) определяются рекурсивно. Особенно наглядно это видно, когда они представлены с помощью синтаксических диаграмм [7, c. 685-703] или в форме Бэкуса-Наура. Подобные определения в рамках конкретного языка программирования могут служить наборами тренировочных заданий по написанию рекурсивных программ и даже простейших рекурсивных трансляторов.
Приведем пример. Идентификатор в Паскале определяется, как и в Фортране, но без ограничений на длину последовательности символов. С помощью синтаксической диаграммы это выглядит так, как это указано на рис.3.7., а в форме Бэкуса-Наура следующим образом (значок “::=” читается как “есть по определению”):
<идентификатор>::=<буква>
<идентификатор>::=<идентификатор><буква>
<идентификатор>::=<идентификатор><цифра>
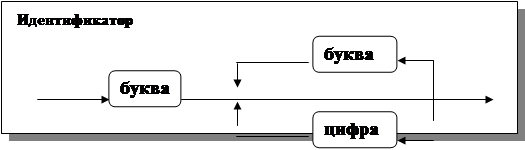
Рис. 3.7. Синтаксическая диаграмма идентификатора (Паскаль)
И в том и в другом случаях идентификатор определяется сам через себя.
3.28 Проблемная ситуацияЗадача 38. При любом ли натуральном n ли рекурсивная функция

равна 1?
Решение. Хотя данная строка и начата со слова “решение”, ответа на поставленный вопрос мы не знаем и, по-видимому, на сегодняшний день его не знает никто. Более того, неизвестно, для любого ли n problem(n) вычисляется за конечное число шагов. Рассмотренную задачу называют 3×n+1 проблемой. Мы включили её в список задач для того, чтобы обратить внимание читателя на следующий факт. Достаточно простые с виду рекурсивные определения функций могут таить в себе глубокие проблемы, решения которых лежат совсем не на поверхности. Тем не менее, конкретные вычисления problem(n) при разных n приводят к одному и тому же значению, равному 1. Ниже приведена рекурсивная программа для проверки истинности утверждения “problem(n)=1” при значениях n из диапазона k1..k2.
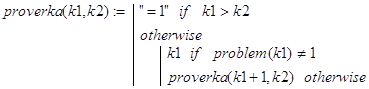
Контрольные примеры.
![]()
![]()
![]()
Похожие работы
... -функций на языке программирования вычислительной среды Mathcad. Все они делятся на три категории: прямые рекурсивные аналоги, частные случаи и обобщения встроенных в Excel финансовых функций. Для первой категории функций и их аргументов используются стандартные обозначения. В иных ситуациях обозначения произвольны. Наличие почти во всех задачах несложно выводимой при определенных навыках, но ...
... ('Поиск путей длины ', PathLen, ' ...'); case TryMove (x, y) of true: WriteLn ('Нашел путь :-)'); false: WriteLn ('Нет путей :-('); end; end; End. Файловый тип. Ввод/вывод. Все рассмотренные ранее типы данных обладали одним общим свойством - число их компонентов конечно и заранее фиксировано. Однако, существует достаточно широкий класс задач, когда количество компонент данных ...
... 100 циклами будет плохочитаемым, длинным и очень объемным. Ну а если там появится небольшая ошибка... (дальше, я думаю, объяснять не стоит). ------------------------- Эту задачу достаточно легко решить с помощью рекурсии. Пишем небольшую функцию: function tree($uid, $conn) { $sql = "SELECT * FROM x_table WHERE parent_id=$uid"; $a = mysql_query($sql, $conn); while($x = mysql_fetch_array($a)) ...
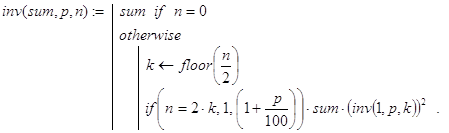
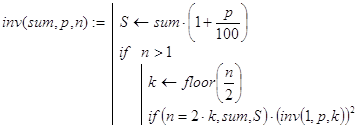
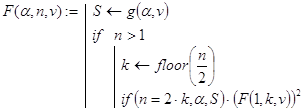
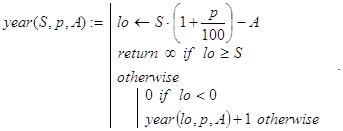
0 комментариев