Навигация
1. fla4(6,2)=5 fla5(6)=5
2. fla4(41,3)T =[16 31] fla5(11)T =[16 31]
3. fla4(1000,5)T=[563 763 802 73] fla5(1000)T=[563 763 802 73]
С. Решение второй задачи Флавия в общем случае.
Пусть функция flav(v,k), где v=(1 2 ... n)T решает поставленную задачу и пусть w - вектор, полученный из v вычеркиванием одного k-го компонента. После каждой такой операции будем организовывать рекурсивный вызов flav(w,k), прекращая вычисления тогда, когда длина вектора станет равной единице. Пусть le - длина вектора v и s=mod(k,le). Нетрудно видеть, что после одного вычеркивания получим:
w=(1 2 ... le-1)T при s=0 ,
w=(2 3 ... le)T при s=1 ,
w=(s+1,s+2,...,le,1,2,...,s-1) при s>=2 .
Поэтому функцию flav(v,k) и обращающуюся к ней функцию fla6(n,k) можно определить следующим образом:
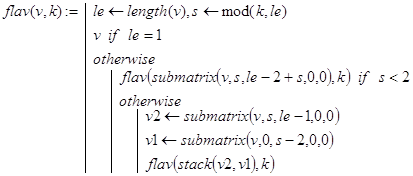
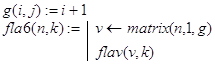
Контрольные примеры.
fla6(10,5)=3 fla6(5,10)=4 fla6(1000,7)=404 .
13.4 Системы счисления
A. Перевод чисел из десятичной системы в p-ичную систему
Не ограничивая общности речь можно вести о неотрицательных числах.Пусть pÎ{2,3,…} и цифры p-ичной системы - это последовательные десятичные числа: 0, 1, ... p-1. Рассмотрим 6 конкретных задач. В трех первых из них речь идет о переводе естественным образом заданных десятичных чисел в p-ичную систему счисления. В следующих трех задачах речь идет о переводе десятичных чисел, цифры которых заданы в виде последовательных компонентов векторов, в p-ичную систему счисления. Во всех случаях результат формируется в виде вектора, компоненты которого p-ичные цифры исходного числа.
Задача 1. Составить программу-функцию перевода целых неотрицательных десятичных чисел m в систему счисления по основанию p.
Решение. Функция dec_p_i(m,p) решает поставленную задачу, используя рекурсивный алгоритм последовательного деления. Результат формируется в виде вектора, компоненты которого p-ичные цифры m.
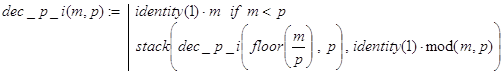
Контрольные примеры.
![]()
![]() .
.
Замечания.
1. Если разряды p-ичного числа необходимо формировать не от старшего разряда, а от младшего и далее, то в программе dec_p_i() первый и второй аргументы функции stack() необходимо поменять местами.
2. При переводе неотрицательных десятичных чисел в конкретную систему счисления, в функции dec_p_i() достаточно иметь один аргумент. Например, перевод в двоичную систему можно осуществлять следующей программой-функцией dec_b_i(m).
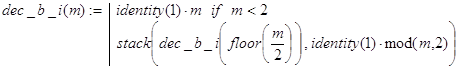
Контрольные примеры.
![]()
Как мы уже отмечали при реализации функций dec_p_i(m,p) и dec_b_i(m) использован рекурсивный вариант алгоритма последовательного деления - выделения цифр p-ичной системы для целых чисел. Пояснений требуют лишь фрагменты вида identity(1)×x. Дело в том, что функция stack() в качестве своих аргументов использует векторы или матрицы. И смысл записи identity(1)×x состоит в превращении скаляра х в матрицу размера 1´1 с элементом x.
Задача 2. Составить программу-функцию перевода правильной неотрицательной десятичной дроби y в систему счисления по основанию p.
Решение. Функция dec_p_f(y,p,k) решает поставленную задачу, используя рекурсивный алгоритм последовательного умножения. Результат формируется в виде вектора с не более чем k (k=1,2,…) компонентами, которые суть p-ичные цифры числа y, начиная от старших разрядов и далее.
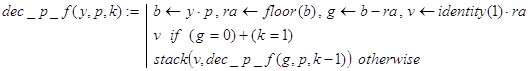
Контрольные примеры.
![]()
Задача 3. Составить программу-функцию перевода неотрицательного действительного десятичного числа a в систему счисления по основанию p (p=2, 3, …).
Решение. Функция dec_p(a,p,k) решает поставленную задачу, осуществляя перевод десятичного числа a в p-ичную систему счисления. Результат вычислений формируется в виде составного вектора. Компоненты этого вектора снова векторы, содержащие соответственно цифры целой и дробной частей числа a в p-ичной системе счисления. Цифры целой и дробной части a возвращаются, начиная со старших разрядов и далее. В дробной части присутствует не более чем k (k=1,2,...) цифр. При вычислениях функция dec_p() обращается к двум рекурсивным функциям dec_p_i() и dec_p_f().
![]()
Контрольные примеры.
![]()
![]()
Задача 4. Пусть m=(v0v1…vn-1)10 - целое десятичное неотрицательное число, цифры которого от старшей и далее заданы последовательными компонентами вектора v=(v0, v1, …,vn-1)T . Составить программу-функцию перевода m в систему счисления по основанию p.
Решение. Функция dec_p_iv(v,p) осуществляет перевод v в p-ичную систему счисления. Результат вычислений формируется, начиная от старших разрядов и далее, в виде вектора, компоненты которого суть p-ичные цифры исходного числа. Функция dec_p_iv(v,p) отличается от ранее рассмотренной функции dec_p_i(v,p) лишь формой представления первого аргумента. Поэтому её вычисление можно свести к вычислению dec_p_i(v,p) с предварительным обращением к рекурсивной функции dv_norm(v), переводящей десятичное число из векторного представления в нормальную форму. Это и сделано ниже.
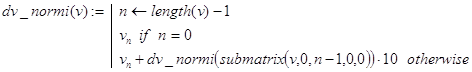
![]()
Контрольные примеры.
![]()
![]()
Задача 5. Пусть y=(.v0v1…vn-1)10 - правильная неотрицательная десятичная дробь, цифры которой от старшей и далее заданы последовательными компонентами вектора v=(v0, v1, …,vn-1)T. Составить программу-функцию перевода y в систему счисления по основанию p.
Решение. Функция dec_p_fv(v,p,k) осуществляет перевод v в p-ичную систему счисления. Результат вычислений формируется, начиная от старших разрядов и далее, в виде вектора длины не более k, компоненты которого суть p-ичные цифры исходного числа. Функция dec_p_fv(v,p,k) отличается от ранее рассмотренной функции dec_p_f(v,p,k) лишь формой представления первого аргумента. Поэтому её вычисление можно свести к вычислению dec_p_f(v,p,k) с предварительным обращением к рекурсивной функции dv_normf(v), переводящей десятичную дробь из векторного представления в нормальную форму. Это и сделано ниже.

![]()
Контрольные примеры.
![]()
![]()
Задача 6. Пусть действительное неотрицательное десятичное число a представлено двумя векторами in и fr, компоненты которых последовательные десятичные цифры, начиная от старшей и далее, соответственно целой и дробной части а. Составить программу-функцию перевода a в систему счисления по основанию p.
Решение. Функция dec_pv(in,fr,p,k) решает поставленную задачу, осуществляя перевод десятичного числа a в p-ичную систему счисления. Результат вычислений формируется в виде составного вектора. Компоненты этого вектора снова векторы, содержащие соответственно цифры целой и дробной частей числа a в p-ичной системе счисления. Цифры целой и дробной части a возвращаются, начиная со старших разрядов и далее. В дробной части присутствует не более чем k (k=1,2,...) цифр. При вычислениях функция dec_p() обращается к двум рекурсивным функциям dec_p_iv() и dec_p_fv().
![]()
Контрольные примеры.
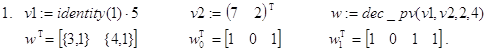

B. Перевод чисел из p-ичной системы в десятичную систему
Пусть pÎ{2,3,…} и цифрами p-ичной системы являются десятичные числа 0,1,... ,p-1. Будем считать, что рассматриваются неотрицательные p-ичные числа, а их цифры от старшего разряда и далее задаются последовательными компонентами векторов. Рассмотрим 3 конкретные задачи.
Задача 7. Пусть m=(v0v1…vn-1)p- целое p-ичное неотрицательное число, цифры которого от старшей и далее заданы последовательными компонентами вектора v=(v0, v1, …,vn-1)T . Составить программу-функцию перевода m в десятичную систему счисления.
Решение. Функция p_dec_i(v,p) решает поставленную задачу, используя рекурсивный алгоритм последовательного деления. Результат формируется в естественной форме.
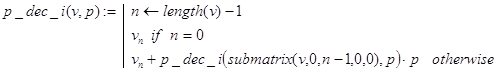
Контрольные примеры.
![]()
![]()
Задача 8. Пусть y=(.v0v1…vn-1)p- правильная неотрицательная десятичная дробь, цифры которой от старшей и далее заданы последовательными компонентами вектора v=(v0, v1, …,vn-1)T . Составить программу-функцию перевода y в десятичную систему счисления.
Решение. Функция p_dec_f(v,p) решает поставленную задачу, используя рекурсивный алгоритм последовательного умножения. Результат формируется в естественной форме.
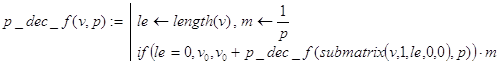
Контрольные примеры.
![]()
![]()
Задача 9. Пусть действительное неотрицательное p-ичное число а представлено двумя векторами in и fr, компоненты которых последовательные p-ичные цифры, начиная от старшей и далее, соответственно целой и дробной части а. Составить программу-функцию перевода a в десятичную систему счисления.
Решение. Функция p_dec(in,fr,p) решает поставленную задачу, осуществляя перевод p-ичного числа a в десятичную систему счисления. Результат вычислений формируется в естественной форме. При вычислениях функция p_dec() обращается к двум рекурсивным функциям p_dec_i() и p_dec_f().
![]()
Контрольные примеры.
![]()
![]()
Замечание. Перевод чисел из p-ичной системы счисления в q-ичную систему (p,qÎ{2,3,…}) можно осуществлять через промежуточную десятичную систему.
Похожие работы
... -функций на языке программирования вычислительной среды Mathcad. Все они делятся на три категории: прямые рекурсивные аналоги, частные случаи и обобщения встроенных в Excel финансовых функций. Для первой категории функций и их аргументов используются стандартные обозначения. В иных ситуациях обозначения произвольны. Наличие почти во всех задачах несложно выводимой при определенных навыках, но ...
... ('Поиск путей длины ', PathLen, ' ...'); case TryMove (x, y) of true: WriteLn ('Нашел путь :-)'); false: WriteLn ('Нет путей :-('); end; end; End. Файловый тип. Ввод/вывод. Все рассмотренные ранее типы данных обладали одним общим свойством - число их компонентов конечно и заранее фиксировано. Однако, существует достаточно широкий класс задач, когда количество компонент данных ...
... 100 циклами будет плохочитаемым, длинным и очень объемным. Ну а если там появится небольшая ошибка... (дальше, я думаю, объяснять не стоит). ------------------------- Эту задачу достаточно легко решить с помощью рекурсии. Пишем небольшую функцию: function tree($uid, $conn) { $sql = "SELECT * FROM x_table WHERE parent_id=$uid"; $a = mysql_query($sql, $conn); while($x = mysql_fetch_array($a)) ...
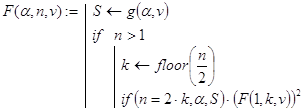
0 комментариев