Генераторы перестановок

13.5 Генераторы перестановок

Ранее в разделе 12.9 мы описали один из алгоритмов получения n! перестановок из элементов множества S={a₀, a₁, …, a_n-1}, где a_k (k=0..n-1) - попарно различные действительные числа. Считая, что S={1,2,…,n}, обсудим еще несколько вариантов рекурсивных алгоритмов генерирования перестановок. Отличаются друг от друга они разными характеристиками: быстродействием, компактностью записи, количеством транспозиций при получении очередной перестановки и т.д.

A. Метод вертикальной прогонки. При S={1} имеем одну перестановку - 1. Если уже имеется последовательность перестановок из n-1 элемента {1,2,…,n-1}, то получить все перестановки из n элементов {1,2,…n} можно способом, который мы будем именовать как “метод вертикальной прогонки” элемента n. Суть его в следующем. Рассмотрим n идентичных экземпляров (групп) последовательностей перестановок из элементов {1,2,…,n-1}. В первом экземпляре в конец каждой перестановки поместим элемент n. Во втором экземпляре этот элемент поместим на предпоследнем месте и т.д. Наконец, в последнем экземпляре поместим n перед первым элементом. На рисунке 13.4 описанная процедура демонстрируется при переходе от n=3 к n=4. Нетрудно понять, что указанные действия любую перестановку из n-1 элемента переводят в некоторую перестановку из n элементов. При этом общее количество полученных перестановок равно n!. Остается показать, что среди них нет совпадающих. Если взять две сгенерированные перестановки внутри одной группы, то они будут различаться друг от друга позициями элементов {1,2,…,n-1} и, значит, не могут быть совпадающими. Если же взять перестановки из разных групп, то позиции элемента n в них будут разными и перестановки опять не могут быть совпадающими. Таким образом, все полученные n! перестановок различны.

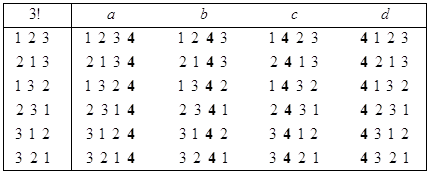
Рис. 13.6. Генерирование перестановок методом вертикальной прогонки.

Описанный алгоритм вертикальной прогонки реализуется рекурсивной программой-функцией permut1(n):

 

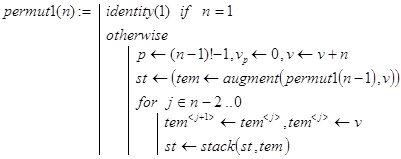
Контрольный пример

 

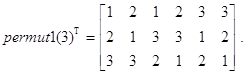
B. Метод последовательного замещения. При S={1} имеем одну перестановку - 1. Если уже имеется последовательность перестановок из n-1 элемента {1,2,…,n-1}, то получить все перестановки из n элементов {1,2,…n} можно способом, который мы будем именовать как “метод последовательного замещения” элемента n. Суть его в следующем. Рассмотрим n идентичных экземпляров (групп) последовательностей перестановок из элементов {1,2,…,n-1}. В первом экземпляре, как и в методе вертикальной прогонки, в конец каждой перестановки поместим элемент n. В каждой перестановке второго экземпляра поменяем местами элементы n и 1. В каждой перестановке третьего экземпляра поменяем местами элементы n и 2 и т.д. Наконец, в последнем экземпляре поменяем местами элементы n и n-1. На рисунке 13.5 описанная процедура демонстрируется при переходе от n=3 к n=4. Нетрудно понять, что указанные действия любую перестановку из n-1 элемента переводят в некоторую перестановку из n элементов. При этом общее количество полученных перестановок равно n!. Остается показать, что среди них нет совпадающих. Если взять две сгенерированные перестановки внутри одной группы, то они обязательно будут различаться друг от друга расположением элементов на позициях от 1 до n-1 и, значит, не могут быть совпадающими. Если же взять перестановки из разных групп, то на последних позициях у них стоят разные элементы и перестановки опять не могут быть совпадающими. Таким образом, все полученные n! перестановок различны.

 

Рис. 13.5. Генерирование перестановок методом последовательного

замещения

Описанный алгоритм последовательного замещения реализуется рекурсивной программой-функцией permut2(n):

 

С. Перестановки в антилексикографическом порядке. На множестве P всех перестановок <x₀,x₁,…,x_n-1> из элементов {1,2,…,n} определим два типа порядка.

Лексикографический порядок на P вводится следующим образом. Для

 "(<a₀,a₁,…,a_n-1>,<b₀,b₁,…,b_n-1>ÎP) (19)

положим

<a₀,a₁,…,a_n-1> <’ <b₀,b₁,…,b_n-1> Û

 $(k ³ 0) [(a_k £ b_k) & "(s < k) [(a_s = b_s)]], (20)

где символ <’ использован в качестве знака лексикографического сравнения перестановок.

Заметим, что если вместо чисел 1,2,…,n использовать буквы с естественным порядком следования их в алфавите, то лексикографический порядок определяет стандартную последовательность, в которой слова длины n появляются в словаре. И это справедливо для алфавитов любых языков.

Аналогично вводится и антилексикографический порядок на P. Для (19) положим

 <a₀,a₁,…,a_n-1> <” <b₀,b₁,…,b_n-1> Û

 $(k £ n-1) [(a_k > b_k) & "(s > k) [(a_s = b_s)]], (21)

где символ <” использован в качестве знака антилексикографического сравнения перестановок.

Построим рекурсивную программу-функцию, генерирующую перестановки элементов {1,2,…n} в антилексикографическом порядке. Соответствующий алгоритм может базироваться на следующих двух утверждениях, непосредственно вытекающих из определения 21.

Утверждение 1. Если множество перестановок P упорядочено антилексикографически, то начальная и конечная перестановки - это соответственно <1,2,…,n> и <n,n-1,…,1>.

Утверждение 2. Упорядоченная антилексикографически последовательность перестановок по значению последнего элемента в них может быть разбита на n блоков длины (n-1)!. При этом q-й блок на последнем месте имеет элемент равный (n-q+1), а первые n-1 позиций этого блока определяют последовательность перестановок множества {1,2,…,n}\{q} в антилексикографическом порядке.

Головная функция permut3(n) решает поставленную задачу. В ней по значению n для рекурсивной программы-функции permu(p) формируется начальная перестановка p. В permu(p) и проводятся все вычисления. На рис. 13.6 представлен результат выполнения permut3(n) при n=3 и n=4. Для n=4 полученные перестановки расположены по столбцам.

 

 

 

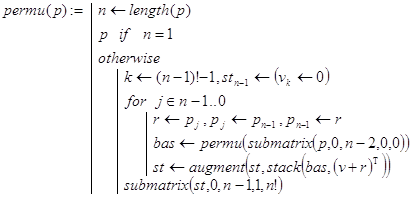
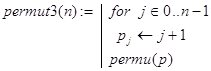
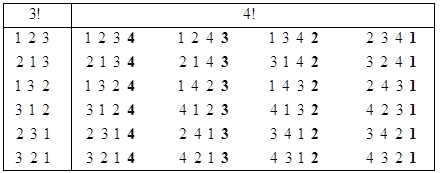
 Рис. 13.6. Генерирование перестановок в антилексикографическом порядке

D. Перестановки в лексикографическом порядке. В предыдущем разделе мы ввели понятие лексикографического порядка. Алгоритм генерирования перестановок в таком порядке и соответствующие программы-функции могут быть построены на идеях, близких к тем, которые использовались при генерировании перестановок в антилексикографическом порядке. Поэтому здесь мы ограничимся лишь приведением соответствующих функций permut(p) и permut4(n) и представим полученный по ним результат вычислений для n=3 и n=4 (см. рис. 13.7). Для n=4 полученные перестановки расположены по столбцам.

 

 

 

Рис. 13.7. Генерирование перестановок в лексикографическом порядке

E. Перестановки c одной транспозицией соседних элементов. В этом пункте рассматривается алгоритм генерирования последовательности перестановок U из элементов множества {1,2,…,n} такой, что любая перестановка U, кроме начальной, получается из предыдущей перестановки одной транспозицией соседних элементов. Проиллюстрируем на примере идею соответствующего алгоритма, приписываемого Джонсону [] и Троттеру []. Предположим, что для элементов {1,2,…,n-1} уже построена требуемая последовательность перестановок U. Тогда из элементов {1,2,…,n} необходимая последовательность может быть построена перемещениями элемента n между начальной и конечной позициями каждой перестановки U. При этом перемещения должны производиться попеременно вперед и назад (n-1)! раз так, как это показано на рис. 13.8.

Рекурсивная программа-функция permut5(n) реализует этот, схематично описанный, алгоритм. На рис. 13.8 приведены полученные по permut5(n) перестановки для n=3 и n=4.

 

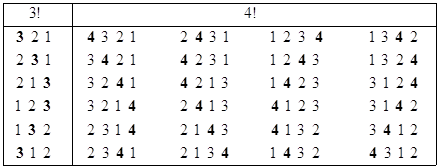
Рис. 13.8. Генерирование перестановок c транспозицией соседних элементов

В заключение автор выражает признательность профессорам. Ваграменко Я.А. и Добровольскому Н.М. за консультации и советы при написании пособия.

Литература

1.  Кнут Д. Искусство программирования для ЭBM. Основные алгоритмы: т. 1, M.: Мир, 1976.

2.  Кнут Д. Искусство программирования для ЭBM. Получисленные алгоритмы: т. 2, М.: Мир, 1977.

3.  Кнут Д. Искусство программирования для ЭBM. Сортировка и поиск: т. 3, М.: Мир, 1978.

4.  Лекции лауреатов премии Тьюринга. М.: Мир, 1985.

5.  Бауэр Ф.Л., Гнац Р., Хилл У. Информатика. Задачи и решения. М.: Мир, 1978 г.

6.  Бауэр Ф.Л., Гооз Г. Информатика. T. 1, М.: Мир, 1990 г.

7.  Бауэр Ф.Л., Гооз Г. Информатика. T. 2, М.: Мир, 1990 г.

8.  Ландау Э. Основы анализа. М.: изд. Иностранной литературы, 1947.

 9. http://www-cs-staff.stanford.edu/~knuth/taocp.html#vol4-{volume4}).