Навигация
6. Задача Иосифа Флавия
С именем известного историка первого века Иосифа Флавия связывают следующую задачу-легенду. В ходе иудейской войны он в составе отряда из 41 воина был загнан римлянами в пещеру. Не желая сдаваться, осажденные воины решили покончить жизнь самоубийством и разработали для этого следующую процедуру. Они выстроились в круг и, начиная отсчет с конкретной позиции, каждый третий должен был убивать себя, пока не останется ни одного человека. Математически одаренный Иосиф считал подобный конец бессмысленным и потому поставил себя и своего друга на такие позиции, что после серии из 39 самоубийств они остались вдвоем, чем и спасли себе жизнь. Что это были за позиции?
Дадим этой задаче-легенде более точную и обобщенную формулировку, освободившись от суицида. При этом будем искать рекурсивные решения двух ниже приведенных задач, различающихся завершением соответствующей процедуры. Подробнее рекурсия как метод решения практических задач обсуждается в следующем параграфе.
Задача 1. По окружности в направлении движения часовой стрелки расположены n последовательных натуральных чисел от 1 до n. При перемещении по числам 1, 2, ... каждое k-ое число (k>1) вычеркивается (удаляется). Этот процесс продолжается до тех пор, пока чисел не станет меньше k. Определить оставшиеся числа.
Задача 2. По окружности в направлении движения часовой стрелки расположены n последовательных натуральных чисел от 1 до n. При перемещении по числам 1, 2, ... каждое k-ое число (k>1) вычеркивается (удаляется). Этот процесс продолжается до тех пор, пока не останется одно число. Определить его.
A. Решение первой задачи Флавия при k=2.
Ниже рассмотрены три варианта A1-A3 решения задачи 1 при k=2, опирающиеся на разные идеи.
A1. Если n=2×s, то после первого прохода по кругу останутся числа: 1, 3, ... 2×s-1 и следующий проход начнется с вычеркивания числа 3. Это все равно, как если бы мы начинали с s последовательных натуральных чисел от 1 до s, но каждое уцелевшее число удваивали и результат уменьшали на 1. Отсюда, если fla1(n) - функция, решающая поставленную задачу, то fla1(1)=1 и
fla1(2×s)=2×fla1(s) - 1 (s³1). (16)
Аналогичные рассуждения показывают, что
fla1(2×s+1)=2×fla1(s) + 1 (s³1). (17)
Величины fla1(n) назовем числами Флавия. Соотношения (16) и (17) сразу же позволяют написать следующую рекурсивную программу-функцию вычисления значений fla1(n).
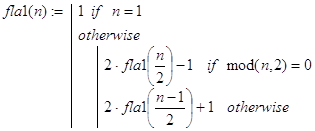
A2. Исследование рекуррентных соотношений (16)-(17) показывает, что
fla1(2s + q)=2×q+1 (s³0, 0£q<2×s) (18)
Отсюда получаем еще один рекурсивный алгоритм для вычисления чисел Флавия (см. ниже). При этом вспомогательная рекурсивная функция power(n,0) вычисляет значение s, удовлетворяющее соотношению (18), то есть уменьшенное на 1 количество цифр двоичного разложения n, а функция fla2(n) непосредственно вычисляет число Флавия для заданного n.
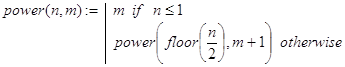
![]()
A3. Еще один способ нахождения чисел Флавия дается программой-функцией flavec(v), где v=(1 2 3 ... n)T - вектор. Подавать такой вектор в качестве аргумента необязательно. Проще обращаться к flavec(v) c помощью функции fla3(n), где по заданному n генерируется соответствующий вектор v. Отметим, что в flavec(v) используется рекурсивный алгоритм непосредственного вычеркивания каждого второго числа. При этом вектор v перестраивается при каждом новом перемещении по кругу.
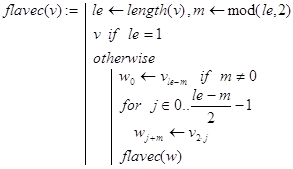
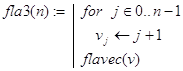
Контрольные примеры.
1. fla1(6)=5fla2(6)=5fla3(6)=5
2. fla1(11)=7 fla2(11)=7 fla3(11)=7
3. fla1(1000)=997fla2(1000)=997fla3(1000)=997
B. Решение первой задачи Флавия в общем случае.
Ниже рассмотрены два варианта B1-B2 решения задачи 1 в общем случае. Первый из них представляет прямое обобщение алгоритма из пункта A3 и реализует рекурсию по каждому вычеркнутому элементу. Во втором варианте рекурсия организована по отдельным проходам по окружности.
B1. Способ A3 решения задачи 1 при k=2 хоть и несколько громоздкий, но он достаточно просто переносится на общий случай. При этом естественно считать k аргументом функции. Тогда решение задачи дает рекурсивная программа-функция flave(v,k), где v=(1 2 3 ... n)T - вектор. Однако проще использовать для этих целей функцию fla4(n,k), формирующую по заданному целому n требуемый вектор v, а затем уже обращающуюся k flave(v,k).
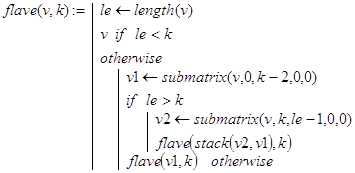

B2. Приведенный ниже способ решения первой задачи Флавия отличается от предыдущего лишь способом организации рекурсии. Здесь она реализована не по каждому вычеркнутому элементу, а по отдельным проходам по окружности. Решение задачи дается программой-функцией flavmek(v,k), где v=(1 2 3 ... n)T - вектор. Однако проще использовать для этих целей функцию fla5(n,k), формирующую по заданному целому n требуемый вектор v, а затем уже обращающуюся к flavmek(v,k). Обратите внимание на используемый в fla5(n,k) метод формирования вектора v.
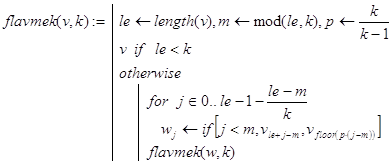
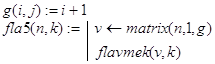
Контрольные примеры.
Похожие работы
... -функций на языке программирования вычислительной среды Mathcad. Все они делятся на три категории: прямые рекурсивные аналоги, частные случаи и обобщения встроенных в Excel финансовых функций. Для первой категории функций и их аргументов используются стандартные обозначения. В иных ситуациях обозначения произвольны. Наличие почти во всех задачах несложно выводимой при определенных навыках, но ...
... ('Поиск путей длины ', PathLen, ' ...'); case TryMove (x, y) of true: WriteLn ('Нашел путь :-)'); false: WriteLn ('Нет путей :-('); end; end; End. Файловый тип. Ввод/вывод. Все рассмотренные ранее типы данных обладали одним общим свойством - число их компонентов конечно и заранее фиксировано. Однако, существует достаточно широкий класс задач, когда количество компонент данных ...
... 100 циклами будет плохочитаемым, длинным и очень объемным. Ну а если там появится небольшая ошибка... (дальше, я думаю, объяснять не стоит). ------------------------- Эту задачу достаточно легко решить с помощью рекурсии. Пишем небольшую функцию: function tree($uid, $conn) { $sql = "SELECT * FROM x_table WHERE parent_id=$uid"; $a = mysql_query($sql, $conn); while($x = mysql_fetch_array($a)) ...
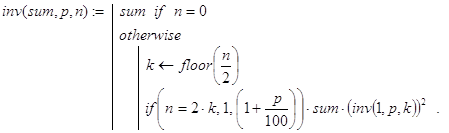
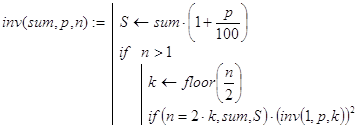
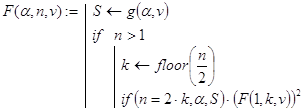
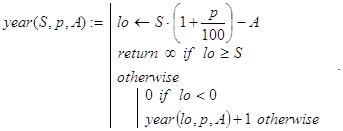
0 комментариев