Передача теплової енергії теплопровідністю (кондукцією)
Теплопровідність вздовж стінок та стержнів
Вільна конвекція в необмеженому просторі
Вільна конвекція в обмеженому просторі
Теплові режими РЕЗ
Максимальна температура РЕЗ
Вибір загальної системи охолодження РЕЗ
Приведення сил
Приведення параметрів дисипації
Коефіцієнт динамічності
Вимушені коливання при періодичному збудженні
Віброзахист обчислювальної техніки
Електромагнітна сумісність радіоелектронних засобів
Застосування еквівалентних електричних схем
Приклад розрахунку еквівалентної схеми
Магнітостатичне екранування
Навигация
Приведення параметрів дисипації
Конструювання обчислювальної техніки
91535
знаков
35
таблиц
66
изображений
2.1.4 Приведення параметрів дисипації
В реальних механічних системах має місце незворотне перетворення механічної енергії в теплову. Це перетворення відбувається за рахунок сил тертя: зовнішніх чи внутрішніх. Елементи, в яких відбувається втрата механічної енергії, називають елементами дисипації (розсіювання).
З точки зору незмінності закону руху системи, дисипативні елементи еквівалентні, якщо вони в будь-який момент часу розсіюють однакову енергію.
Розсіювання механічної енергії в пружному елементі пов’язане з його нелінійністю (рис. 2.5). Графіки F(x) при прямій і зворотній деформації відрізняються між собою. Введемо такі позначення:
↑ A – робота сили при прямій деформації.
Їй відповідає горизонтально заштрихована площа;
↓ А – робота сили при зворотній деформації.
Їй відповідає вертикально заштрихована площа;
↑↓А – розсіяна енергія, А↑↓= А↑–А↓.
Рис. 2.5. Характеристика F(x) нелінійного елемента
Коефіцієнт дисипації ψ вводиться як відношення
ψ = А↑↓ / А↑, (2.6)
де ψ – безрозмірний коефіцієнт, який визначає відносну частину розсіяної енергії від енергії, що накопичує пружний елемент.
Енергія, яку розсіює механічна система в пружних елементах дорівнює сумі енергій, що розсіює кожний дисипативний елемент. Умова незмінності розсіяної енергії при переході до одного приведеного елемента дисипації відображається рівнянням:
.
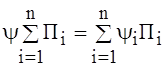Приведений коефіцієнт дисипації
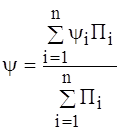. (2.7)
При паралельному з’єднанні елементів дисипації формула (2.7) має вигляд:
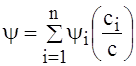. (2.8)
При послідовному з’єднанні формула (2.7) має вигляд:
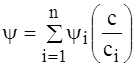. (2.9)
2.2 Вільні коливання одномасової системи
Розглянемо одномасову модель механічної системи (рис. 2.6).
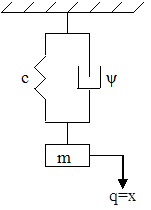
Рис. 2.6. Одномасова система
В стані рівноваги пружина розтягнута. Пружна сила врівноважує силу тяжіння mg. Стан рівноваги вибирається як початкове положення. Якщо систему вивести із стану рівноваги, вона здійснює коливання відносно початкового положення. Згідно закону Ньютона:
, (2.10)
де пружна сила cq та сила тертя 
направлені відповідно проти переміщення q та проти напрямку руху, тобто проти швидкості 
Рівняння (2.10) запишемо в канонічному вигляді:
, (2.11)
де 
– кутова частота власних коливань; n = b/2m, де b – кінематичний коефіцієнт тертя.
Рівняння (2.11) – лінійне однорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами. Воно описує вільні коливання. В реальних механічних системах значення коефіцієнта тертя b практично не впливає на частоту вільних коливань. Тому розв’язок рівняння (2.11) має вигляд:
q = e–nt (С1·sin kt + С2·cos kt) = e–ntA·cos(kt - j), (2.12)
де 
; sin j = С1/A; cos j = С2/A.
Сталі інтегрування С1 і С2 визначаються з початкових умов коливного процесу 
і qo = q(0):
С2 = qo; С1 = (
+ nqo)/ k. (2.13)
Завдяки множнику е–nt навіть при малому значенні n система з часом припиняє свої вільні коливання:
при t®¥ значення е–nt =1/ent ® 0 (рис. 2.7).
 |
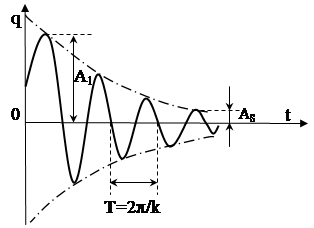Рис. 2.7. Затухаючі вільні коливання
Вільні коливання відіграють дуже важливу роль у визначенні приведених параметрів механічної системи експериментальним способом.
Алгоритм експерименту:
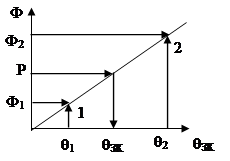
1. Будується статична характеристика F = F(q) (рис.2.8) і визначається коефіцієнт жорсткості с = F / q.
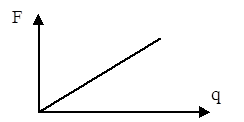
Рис. 2.8. Статична характеристика F(q)
2. Збуджуються вільні коливання. Експериментально визначають Т або f й знаходять кругову частоту власних коливань:
k = 2π / T = 2πf.
3. Знаходять приведену масу:
4. Збуджують власні коливання і спостерігають їх затухання, вимірюють амплітуду А1 і Аs та визначають:
,
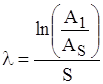де S – число коливань, що спостерігається (звичайно S = 10, 100, 1000, ...)
5. Визначають приведений коефіцієнт затухання:
n = 2λ / T.
2.3 Вимушені коливання при гармонічному збудженні
Розглянемо одномасову модель механічної системи, яка здійснює вимушені коливання під дією гармонічної сили (рис. 2.9):
F(t) = F0 cos ωt.
При F=0 та q=0 система має стан стійкої рівноваги.
Згідно закону Ньютона складаємо баланс сил:
.
В канонічній формі рівняння набуває вигляду
, (2.14)
де 2n=b/n, k2 =c/m, 
.
Рис. 2.9. Вимушені коливання
Це лінійне неоднорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами. Його загальний розв’язок qЗ.Н. шукають у вигляді:
qЗ.Н. = qЗ.О. + qЧ.Н., (2.15)
де qЗ.О. – загальний розв’язок однорідного рівняння (при f0=0);
qЧ.Н. – частковий розв’язок неоднорідного рівняння.
Оскільки при t®¥ вільні коливання затухають, то достатньо визначити частковий розв’язок qЧ.Н.(t). Його шукаємо у вигляді гармоніки, бо гармонічною є права частина рівняння (2.14).
qЧ.Н. = Acos(ωt-j) = С1sin ωt+С2cos ωt. (2.16)
Сталі інтегрування відповідають усталеному режиму вимушених коливань, які визначають за таким алгоритмом. Диференціюємо рівняння (2.16) один, а потім ще один раз і одержимо відповідно та 
, які підставляємо в рівняння (2.14). З умови тотожної рівності лівої і правої частини, прирівнюючи коефіцієнти при cos ωt та sin ωt, одержимо два алгебраїчні рівняння з двома невідомими А і tg φ. Остаточно одержимо:
, 
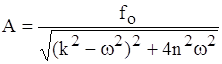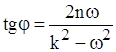. (2.17)
Похожие работы
... до студентів інформацію зрозуміло та цікаво. 7.3. 20.03.09 Робота з навчально-методичною літературою. Відвідування бібліотеки. Підготовка до практичних робіт з дисципліни "Основи конструювання ОТ" 7.4. 24.03.09 Обговорення з керівником асистентської практики. 7.5 25.03.09 Участь в методичному семінарі кафедри. Ознайомились з науково-дослідною роботою ...
... "ВНІЇЕМ-3", а також надшвидкодіюча БЕСМ-6 з продуктивністю 1 млн операцій в секунду. 2.3 Третє покоління комп'ютерів Поява інтегрованих схем започаткувала новий етап розвитку обчислювальної техніки - народження машин третього покоління. Інтегрована схема, яку також називають кристалом, являє собою мініатюрну електронну схему, витравлену на поверхні кремнієвого кристала площею приблизно 10 ...
... рахунку всі науково-технічні поняття є відображенням технічного об'єкта. Поняття “технічний об'єкт” і “об'єкт технічної науки” виконують різну методологічну функцію у філософському аналізі техніки і науково-технічного пізнання. У понятті “технічний об'єкт” фіксується реально змінювана в практиці сторона об'єктивного світу. Технічний об'єкт відображається у філософських, суспільних, природних і ...
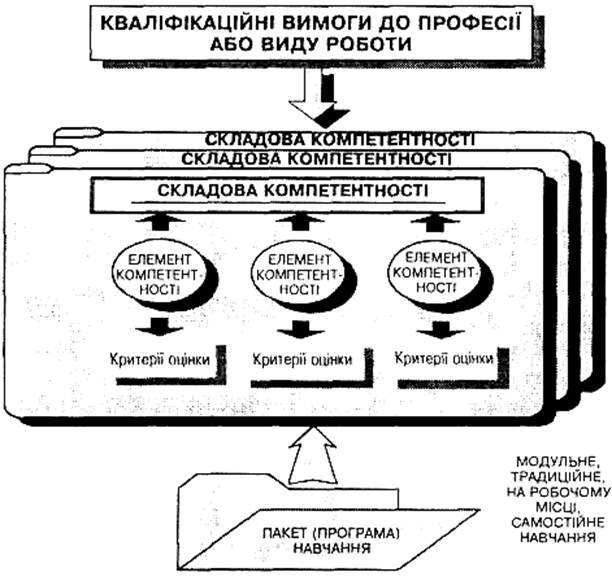
... ів з професій (Типові навчальні плани і програми, кваліфікаційні характеристики і т. ін.), що входять до цього переліку, практично робить неможливим перехід на підготовку робітничих кадрів згідно з означеним документом, оновлення змісту професійно-технічної освіти. Сьогодні, на нашу думку, першочерговим завданням у розв'язанні проблеми розробки і впровадження державних стандартів профтехосвіти у ...
0 комментариев