Суждение А общеутвердительное. Его структура «все S есть Р». Рассмотрим 2 случая

1.         суждение А общеутвердительное. Его структура «все S есть Р». Рассмотрим 2 случая.

·          В суждении «все караси – рыбы» субъектом является понятие «карась» (S), а предикатом понятие «рыба» (Р). Квантор общности «все».

Субъект распределен, т.к. речь идет о всех карасях, т.е. его объем полностью включен в объем в объем предиката. Предикат не распределен т.к. в суждении речь идет лишь о той части объема предиката которая совпадает с объемом субъекта. Если объем Р > объема S, то Р не распределен.

·          В суждении «все квадраты – равносторонние прямоугольники» термины такие: S – квадрат, Р – равносторонний прямоугольник, квантор общности – «все» . В этом суждении S распределен, т.к. их объемы полностью совпадают.

2.         Суждение I частноутвердительное . Его структура: «некоторые S есть Р». 2 случая.

·          В суждении «некоторые школьники» футболисты» термины такие: S- школьники, Р- футболисты, квантор существования – некоторые. Субъект не распределен, т.к. в нем мыслится только часть школьников, т.е. объем субъекта лишь частично включается в объем предиката. Предикат тоже не распределен, т.к. он также лишь частично включен в объем субъекта. (только некоторые футболисты являются школьниками).

Если понятия S и Р перекрещиваются, то Р не распределен.

·          В суждении «некоторые писатели – драматурги». Термины такие: S- писатель, Р – драматурги, квантор существования – некоторые. Субъект не распределен, т.к. в нем мыслится только часть писателей, т.е. объем субъекта лишь частично включается в объем предиката. Предикат распределен, т.к. объем предиката полностью входит в объем субъекта. Т.О. Р распределен, если объем Р меньше объема S,что бывает в частных выделяющих суждениях.

3.суждение Е общеотрицательное. Его структура: «ни одно S не есть Р. Например, ни один лев не есть травоядное животное.

В нем термины такие: S-лев, Р- травоядное животное», квантор общности – ни один. Здесь объем субъекта полностью исключается из объема предиката и наоборот. Поэтому и S, и Р распределены.

4. суждение О частноотрицательное. Его структура: некоторые S не есть Р.

Например, некоторые учащиеся не являются спортсменами». В нем такие термины: S –учащиеся, Р- спортсмены, квантор существования – некоторые.

Субъект не распределен, т.к. мыслится лишь часть учащихся, а предикат распределен, ибо в нем мыслятся все спортсмены, ни один из которых не включен в ту часть учащихся, которая мыслится в субъекте.

Итак, S распределен в общих суждениях и не распределен в частных; Р всегда распределен в отрицательных суждениях, в утвердительных же он распределен тогда, когда по объему Р S.

 

Сложные суждения, их состав и виды. Таблицы истинности сложных суждений.

Сложные суждения образуются из простых суждений с помощью логических связок: конъюнкции, дизъюнкции, импликации, эквиваленции и отрицания. Таблицы истинности этих логических связок следующие:

а	В
И	И	И	И	Л	И	И
И	Л	Л	И	И	Л	Л
Л	И	Л	И	И	И	Л
Л	Л	Л	Л	Л	И	И

Буквы а, в, с- переменные, обозначающие суждения; «и» -истина, «л»-ложь.

Таблицу истинности для конъюнкции можно разъяснить на следующем примере:

«(учитель конкретный) является хорошим педагогом (а) и учится заочно (в)». Она будет истинна в том и только в том случае, если суждения аи в оба истинны. Это и отражено в первой строке. Если же (а) ложно или (в) ложно либо и а, и в ложны, то вся конъюнкция обращается в ложь.

Суждение 2увеличение рентабельности» достигается путем повышения производительности труда (а) или путем снижения себе стоимости продукции (в)- пример нестрогой дизъюнкции. Дизъюнкция называется нестрогой, если ее члены не исключают друг друга. Такое высказывание истинно в том случае, когда истинно хотя бы одно из 2-х суждений, и ложно, когда оба суждения ложны

Члены строгой дизъюнкции исключают друг – друга. Это можно разъяснить на примере6 «я поеду на юг на поезде (а) или полечу на самолете (в).» я не могу одновременно ехать на поезде и лететь на самолете. Строгая дизъюнкция истинна тогда, когда истинно лишь одно из 2-х простых суждений.

Таблицу для импликации можно разъяснить на таком примере: «если через проводник пропустить электрический ток (а), то проводник нагреется (в)». Импликация истинна всегда, кроме одного случая, когда первое суждение истинно, а 2- е ложное. Действительно, не может быть так, чтобы по проводнику пропустили электрический ток. Т.е. суждение (а) было истинным, а проводник не нагрелся, т.к. суждение (в) было ложным

Эквиваленция в таблице характеризуется так: а=в истинно в тех и только в тех случаях, когда и а, и в либо оба истинны, либо оба ложны

Отрицание суждения а (т.е.а) характеризуется так: если а истинно, то его отрицание ложно, и если (а) ложно, то (а) истинно.

Способы отрицания суждений

2 суждения называются отрицающими или противоречивыми друг другу, если одно из них истинно, а другое обязательно ложно.(они не могут одновременно быть истинными или одновременно ложными).

Отрицающими являются следующие пары суждений:

а	а
И	Л
Л	И

1.         А-О . Все S есть Р и некоторые S не есть Р.

2.         Е-I. Ни одно S не есть Р и некоторые S есть Р.

3.         это S есть Р и это S не есть Р.

Операцию отрицания в виде образования нового суждения из данного следует отличать от отрицания, входящего в состав отрицательных суждений. Существует 2 вида отрицания: внутреннее и внешнее. Внутренне указывает на несоответствие предиката субъекту ( связка: не есть, не суть, не является).

Например, «некоторые люди не имеют высшего образования». Внешнее отрицание означает отрицание всего суждения. Например, «не верно, что в Москве протекает река Нева».

Итак, 1) конъюнкция истинна тогда, когда оба простых суждения истинны.

2) строгая дизъюнкция (а в) истинна тогда, когда только одно простое суждение истинно.

3) нестрогая дизъюнкция (а в) истинна тогда, когда хотя бы одно простое суждение истинно.

4) импликация истинна во всех случаях, кроме одного: когда (а) истинно, а (в) ложно.

5) эквиваленция (а ) истинна тогда, когда оба суждения истинны или оба ложны

6) отрицание (а) истинны дает ложь, и наоборот.

Отношения между суждениями по истинности. Логический квадрат

 

Суждения, как и понятия, делятся на сравнимые (имеют общий субъект или предикат) и несравнимые. Сравнимые суждения делятся на совместимые и несовместимые.

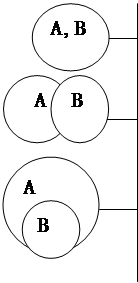
Совместимые выражают одну и ту же мысль полностью или лишь в некоторой части отношения совместимости: эквивалентность, логическое подчинение, частичное совпадение. Совместимые эквивалентные суждения выражают одну и ту же мысль в различной форме. Например, «Юрий Гагарин первый космонавт», и «Юрий Гагарин первым полетел в космос». Субъект здесь один и тот же, а предикаты различные по форме, но одинаковые по смыслу.

В 2-х эквивалентных суждениях: «Михаил Шолохов- лауреат нобелевской премии» и « автор романа «тихий дон»- лауреат нобелевской премии»- одинаковыми являются предикаты, а различными по форме выражения, но тождественными понятиями- субъекты.

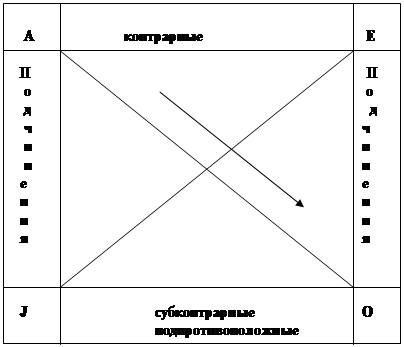
Совместимые суждения, находящиеся в отношении логического подчинения, имеют общий предикат; понятия, выражающие субъекты 2-х таких суждений, так же находятся в отношении логического подчинения. Отношения между суждениями по истинности принято схематически изображать в виде «логического квадрата»

Для суждений А и I, а также Е и О, находящиеся в отношении логического подчинения, истинность общего суждения определяет истинность частного, подчиненного суждения, но ложность общего суждения оставляет частное суждение неопределенным. Истинность частного суждения оставляет общее суждение неопределенным. Ложность частного суждения обуславливает ложность общего суждения. Если истинно суждение «ни одна трапеция не является сферическим телом», то будет истинным и суждение «некоторые трапеции не являются сферическими телами». Умозаключение подчиненному ему частному суждению всегда будет давать истинное заключение.

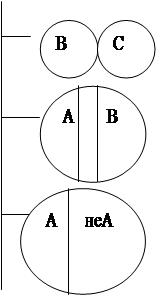
В отношении частичного совпадения (субконртакности) находятся 2 таких совместимых суждения I и О, которые имеют одинаковые субъекты и одинаковые предикаты, но различаются по качеству. Например, I –«некоторые свидетели дают истинные показания» и О – «некоторые свидетели не дают истинных показаний». Оба они одновременно может быть истинными, но не могут быть одновременно ложными. Если одно из них ложно, то другое неопределенно (оно может быть истинным, либо ложным).

 Отношения несовместимости: противоположность, противоречие. По логическому квадрату в отношении противоположности (контрарности) находятся суждения А и Е. два суждения: А- «все люди трудятся добросовестно» и Е – «ни один человек не трудится добросовестно» - оба ложны. Но А и Е не могут быть оба истинными. Если одно из противоположных суждений истинно, то другое будет ложным.

Итак, из истинности, одного из противоположных суждений вытекает ложность другого, но ложность одного из них оставляет другое суждение неопределенным.

В отношении противоречия (контрадикторности) находятся суждения А и О, а так же Е и I, противоречащих суждения не могут быть одновременно ложными. Если в настоящее время истинно суждение I- «некоторые летчики – космонавты», то ложным будет суждение «ни один летчик не является космонавтом».

Закономерности, выражающие отношения между суждениями, по истинности, имеют большое познавательное значение, т.к. они помогают избежать ошибок при непосредственных умозаключениях, производимых из одной посылки (одного суждения).

Модальные суждения, их состав и виды

В логике рассматривались, простые суждения, которые называются ассерторическими, а так же сложные суждения, составленные из простых. В них утверждается или отрицается наличие определенных связей между предметом и его свойствами или констатируется отношение между двумя или большим числом предметов. Например, «школьники – учащиеся», «в прямоугольном треугольнике сумма квадратов ( катетов равна квадрату гипотенузы, т.е. а+в =с». Общая форма суждений: «S есть ( не есть) Р, то S есть (не есть) Р».

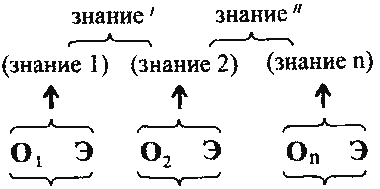
В этих ассерторических суждениях не установлен характер связи между субъектом и предикатом. Характер связи между субъектом и предикатом или между отдельными простыми суждениями в сложном суждении раскрывается в модальном суждении. Из выше перечисленных суждений можно образовать такие, например, модальные суждения: «несомненно, что все школьники – учащиеся», «доказано, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы». Отсюда видно, что модальные суждения не просто утверждают или отрицают некоторые связи, а дают оценку этих связей с какой – то точки зрения.

О предмете А можно просто сказать, что он имеет свойство В (это будет ассерторическое суждение). Но можно сверх того уточнить, является ли эта связь А и В необходимой , или наоборот, случайной; хорошо ли, что А есть В или это плохо; доказано, что а есть В или не доказано. В результате таких уточнений мы получакм модальные суждения различных типов. Приведем другие примеры модальных суждений: «возможно, на марсе есть жизнь», «при красном свете светофора проезд транспорта запрещен».

Структура простых модальных суждений такая: М (S есть Р) или М (S не есть Р), где М обозначает модальное понятие.

 Но как было уже сказано , модальными могут быть и сложные суждения. Если а ив – простые суждения, то из сложных ассерторических суждений: а в, а в, а в, а в, а= - можно получить соответствующие сложные модальные суждения:

М(а в); М(а в); М(а в); М(а в); М(а в). В каждом из пяти типов сложных модальных суждений модальное понятие М может быть заменен его разновидностями, например, из сложного ассерторического суждения «если в почву внести удобрения, то урожай повысится» можно получить такие модальные суждения: «доказано, что если в почву внести удобрения, то урожай повышается», «хорошо, что если в почву внести удобрения, то урожай повышается и др.»

Модальными простыми суждениями называют простые суждения, выражающие связь между субъектом и предикатом с помощью модальных понятий.

Модальными сложными суждениями называют сложные суждения, выражающие связь между составляющими их простыми суждениями с помощью модальных понятий.

В настоящее время современной модальной логикой изучены многие виды модальностей, и те из них которые сравнительно хорошо изучены систематизированы в следующей таблице, предложенной А.А. Ивиным.

Логические модальности	Онтологические модальности	Эпистемические модальности Знание убеждение
Логически необходимо	Онтологически необходимо	Доказуемо	Полагает (убежден)
Логически случайно	Онтологически случайно	Неразрешено (непроверяемо)	Сомневается
Логически невозможно	Онтологически невозможно	опровержено	Отвергает
Логически возможно	Онтологически возможно		Допускает

Термин «эпистемическая модальность» происходит от греческого слова «эпистем» означавшего внешний тип несомненного, достоверного знания.

Термин «деонтический» с греческого означает «обязанность». Термин «аллетический» - необходимость.

Деонтические модальности	Аксиологические модальности		Временные модальности
	абсолютные	сравнительные	Абсолютные	сравнительные
Обязательно	Хорошо	Лучше	Всегда	Раньше
Нормативно – безразлично	Аксиологически безразлично	Равноценно	Только иногда	Одновременно
Запрещено	плохо	хуже	никогда	позже
разрешено

Иногда в дополнение к трем основным модальным понятия и вводится четвертое, которое может употребляться вместо них.

Логические и онтологические модальности объединяются в общий вид –аллетические модальности. Они включают такие модальные понятия: необходимость и случайность, возможность и невозможность. Слова «необходимо», «возможно», «случайно» в обыденном языке употребляются в самых различных смыслах.

Алетические модальности обозначаются так: « А» -«необходимо А»; « А» -« А»- «случайно А; « А»- «возможно А»; « А»- «невозможно А» (знак « «- отрицание). Иногда их обозначают так:» « - «необходимо р», «Мр» - возможно р»

Формулы взаимосвязи алегичеких модальностей.

1. («если необходимо, что А, тоА») 2. («если А, то возможно, что А») 3. («необходимо, что А, тогда и только тогда, когда невозможно, что не а») 4. («возможно, что А, тогда и только тогда, когда необходимо, что не А»)

Умозаключение как форма мышления. Структура и общее правило умозаключения. Типы и виды умозаключений

 

Формами мышления является понятие, суждения и умозаключения. С помощью многообразных видов умозаключений мы можем получать новые знания. Построить умозаключение можно при наличии одного или нескольких истинных суждений, поставленных во взаимную связь. Возьмем пример умозаключения:

Все углероды горючи

Алмаз –углерод

Алмаз горюч

Структура всякого умозаключения включает посылки (истинные суждения), заключение и логическую связь между посылками и заключением. Логический переход от посылок к заключению называется выводом. В приведенном примере 2 первых суждения, стоящих над чертой, являются посылками; суждение: «алмаз горюч» является заключением. Для того что бы проверить истинность заключения «алмаз горюч», вовсе не нужно сжигать алмаз. Заключение о горючести алмаза с полной достоверностью можно получить с помощью умозаключения, опираясь на истинность посылок и соблюдение правил вывода.

Умозаключение- форма мышления, в которой из одного или нескольких истинных суждений на основании определенных правил вывода получается новое суждение, с необходимостью или определенной степенью вероятности следующее из них. Процесс получения заключений из посылок по правилам дедуктивных умозаключений называется выведением следствий.

Выведение следствий из данных посылок широко распространенная логическая операция.

Логическое следствие из данных посылок есть предложение, которое не может быть ложным, когда эти посылки истинны.

Пример, нам даны 3 посылки:

1)         «если Иван- брат Марьи или Иван- сын Марьи, то Иван и Марья- родственники».

2)         «Иван и Марья –родственники»

3)         «Иван не сын Марьи». Можно ли из них вывести логическое следствие, что «Иван – брат Марьи?» многим кажется, что такое логическое заключение из данных трех посылок будет истинным. Что бы проверить это, следует составить формулу этого умозаключения. Обозначим суждение «Иван – брат Марьи» буквой а, суждение «Иван –сын Марьи» -в, и суждение «Иван и Марья – родственники»- с. Над чертой -3 данные посылки, под чертой – предполагаемое заключение:

Объединив 3 посылки в конъюнкцию и присоединив к ним посредством знака предполагаемое заключение а, получим:

Теперь составим для этой формулы таблицу.

а	в	с	В	а в	(а в) с	(а в) с с в	(а в) с с в а
И	И	И	Л	Л	И	Л	И
И	И	Л	Л	Л	И	Л	И
И	Л	И	И	И	И	И	И
И	Л	Л	И	И	Л	Л	И
Л	И	И	Л	И	И	Л	И
Л	И	Л	Л	И	Л	Л	И
Л	Л	И	И	Л	И	И	Л
Л	Л	Л	И	Л	И	Л	Л

В последней колонке формула в одном случае принимает значение «ложь», значит, она не является законом логики. Следовательно, из данных трех посылок не следует с необходимостью заключение, что «Иван – брат Марьи». Иван может быть племянником марь, или отцом Марьи, или дядей Марьи, или каким – либо другим ее родственником.

Этот пример показывает, что эффективность средств математической логики видна тогда, когда средствами, традиционной формальной логики трудно установить вытекает ли какое – либо следствие из данных посылок или нет, особенно, когда мы имеем дело с большим числом посылок.

Умозаключения делятся на дедуктивные, индуктивные и Все окуни дышат жабрами я по аналогии. Умозаключения могут быть логически необходимыми, т. е. давать истинное заключение, и вероятными ( правдоподобными), т.е. давать истинное заключение, а лишь с определенной степенью вероятности следующее из данных посылок.

Итак,

1)         формами мышления являются не только понятия и сужения, но и умозаключения.

2)         Структура умозаключения включает посылки, заключение и логическую связь между посылками и заключением.

3)         Умозаключения делятся на дедуктивные, индуктивные и умозаключения по аналогии.

 

Дедуктивные умозаключения. Типы и виды Д.У. непосредственные умозаключения, их виды

 

Дедуктивное умозаключение (ДУ)-такое, в котором заключение необходимо следует из посылок, выражающих знания большей степени общности, и которое само является знанием меньшей степени общности.

Например, все рыбы дышат жабрами.

Все окуни – рыбы.

Все окуни дышат жабрами.

Здесь первая посылка «все рыбы дышат жабрами» является общеутвердительным суждением и выражает большую степень обобщения по сравнению с заключением, так же являющимся общеутвердительным суждением «Все окуни дышат жабрами». Мы строим умозаключение от признака, принадлежащего роду («рыба»), к его принадлежности к виду «окунь», т.е. от общего класса к его частному случаю, к подклассу.

Умозаключение дает истинное заключение, если исходные посылки истинны и соблюдены правила вывода. Правила вывода или правила преобразования суждений позволяют переходить от посылок определенного вида к заключениям также определенного вида. Так, наблюдая движение луны и солнца и делая логические выводы из этих наблюдений, люди еще в древности умели логически выводить из них достаточно точные предсказания о поступлении солнечных и лунных затмений.

Различают правила прямого вывода и правила непрямого (косвенного) вывода.

Правила прямого вывода позволяют из имеющихся истинных посылок получить истинное заключение. Правила непрямого вывода позволяют заключать о правомерности некоторых выводов из правомерности других выводов.

На основе правил прямого вывода построены дедуктивные умозаключения. Типы ДУ такие: выводы, зависящие от субъектнопредикатной структуры суждений; выводы, основанные на логических связях между суждениями.

Непосредственными умозаключениями называются ДУ, делаемые из одной посылки. К ним относятся следующие: превращение обращение, противопоставление предикату и умозаключения по «логическому квадрату»

·          Превращение – вид непосредственного умозаключения, при котором изменяется качество посылки без изменения ее количества. По качеству связки категорические суждения делятся на утвердительные и отрицательные. При этом частноутвердительное суждение превращается в частноотрицательное и наоборот, а общеутвердительное суждение – в общеотрицательное и наоборот. Превращение строится двумя способами:

1)         путем двойного отрицания, которое ставится перед связкой и перед предикатом: S есть Р. – S не есть не –Р.

Подлежащие – главные члены предложения – ни одно подлежащее не является не главным членом предложения;

2)         отрицание можно переносить из предиката в связку.

S есть не Р. – S не есть Р.

Все галогены являются неметаллами. – ни один галоген не является металлом.

Превращению подлежат все 4 вида суждения: А, Е,I,О.

1.         А-Е.

Структура: все S есть Р.- ни одно S не есть не –Р.

Все волки – хищные животные. – ни один волк не является нехищным животным.

2.         Е-А.

Ни одно S не есть Р. – все S есть не –Р.

 Ни один многогранник не является плоской фигурой. – все многогранники не являются неплоскими фигурами.

3.         I –О

 Некоторые S есть Р. – некоторые S есть не -Р. Некоторые грибы съедобны. Некоторые грибы не являются несъедобными.

 4.О – I. Некоторые S не есть Р. – некоторые S есть не -Р. Некоторые члены предложения не являются главными. – некоторые члены предложения являются неглавными.

·          Обращением называется такое непосредственное умозаключение, в котором в заключении субъектом является предикат, а предикатом – субъект исходного суждения, т.е. происходит перемена мест субъекта и предиката при сохранении качества суждения.

Примеры:

1.         все дельфины –млекопитающие. – некоторые млекопитающие являются дельфинами.

2.         все развернутые углы – углы, стороны которого составляют одну прямую. –все углы, стороны которого составляют одну прямую, являются развернутыми углами.

3.         некоторые школьники являются филателистами – некоторые филателисты являются школьниками.

4.         некоторые музыканты – скрипачи. – все скрипачи являются музыкантами.

Обращение бывает 2-х видов: простое или чистое (примеры 2 и3) и обращение с ограничением (примеры 1 и 4).

Обращение будет чистое, или простое, тогда когда и S, и Р исходного суждения либо оба распределены, либо оба не распределены. Обращение с ограничением бывает тогда, когда в исходном суждении субъект распределен, а предикат не распределен, или наоборот, S не распределен, а Р распределен.

·          Противопоставление предикату.

Это такое непосредственное умозаключение, при котором в новом суждении субъектом является понятие, противоречащее предикату исходного суждения, а предикатом является субъект исходного суждения, вместе с этим связка меняется на противоположную.

Иными словами мы делаем т.о.:

1.         вместо Р берем не Р;

2.         меняем местами S и не Р:

3.         связку меняем на противоположную.

Например, дано суждение: «все львы -хищные животные». В результате противопоставления предикату получим суждение: «ни одно нехищное животное не является львом».

Противопоставление предикату можно рассматривать как результат 2- х последовательных непосредственных умозаключений – сначала превращение, затем обращения превращенного суждения.

Противопоставление предикату для различных видов суждений осуществляется так:

1.         А. все S есть Р.—ни одно не –Р не есть S. Все металлы электропроводны. – ни один не электропроводник не является металлом.

2.         Е. ни одно S не есть Р. – некоторые не Р есть S.ни один красный мухомор не является съедобным грибом – некоторые несъедобные грибы есть красные мухоморы.

3.         О. некоторые S не есть Р.- некоторые не Р есть S. Некоторые преступления не являются умышленными. –некоторые неумышленные деяния являются преступлениями.

4.         I. Из частноутвердительного суждения необходимые выводы не следуют.

Задача.

Сделать превращение, обращение и противопоставление предиката для следующего суждения:

«все грибы – растения».

Это суждение вида А.

Превращение –«ни один гриб не является не растением.

Обращение (с ограничением) –некоторые растения являются грибами.

Противопоставлению предикату –ни одно не растение не есть гриб.

Все виды непосредственных умозаключений дают нам новое знание особенно умозаключение, называемое противопоставлением предикату.

·          Умозаключение по логическому квадрату.

На основании отношений между суждениями А, Е, I, О можно строить достоверные непосредственные выводы.

Например, пусть дано истинное суждение А: «все тюлени –ластоногие». Из него можно сделать следующие выводы:

1)         суждение Е: ни один тюлень не является ластоногим –ложное суждение.

2)         Суждение I: некоторые тюлени являются ластоногими –истинное суждение

3)         Суждение О: некоторые тюлени не являются ластоногими – ложное суждение

Итак, непосредственные умозаключения – дедуктивные умозаключения, делаемые из одной посылки. К ним относятся: превращение, обращение, противопоставление предикату и умозаключение по логическому квадрату.

 

Логические ошибки: софизмы и паралогизмы. Понятие о логическом парадоксе

 

Непреднамеренная ошибка, допущенная человеком в мышлении, называется паралогизмом. Преднамеренная ошибка, совершаемая с целью запугать противника и выдать ложное суждение за истинное, называется софизмом.

Софистами, называют людей, которые пытаются выдать ложь за истину путем различных ухищрений.

Математические софизмы собраны в целом ряде книг. Так, Ф.Ф. Нагибин формулирует следующие математические софизмы:

1)         5=6

2)         2*2=5

3)         Все числа равны между собой и др.

Парадокс –это рассуждение, доказывающее как истинность, так и ложность некоторого суждения, иными словами, доказывающее как это суждение, так и его отрицание. Парадоксы были известны еще в древности. Примерами парадоксов является: «куча», «лысый», 2каталог всех нормальных каталогов», «мэр города», «генерал», «брадобрей».

Парадокс «куча». Разница между кучей и не кучей – не в одной песчинке. Пусть у нас есть куча (например, песка). Начинаем от нее брать каждый раз по одной песчинке, и куча остается кучей. Продолжаем этот процесс. Если 100 песчинок куча, то 99 – тоже куча и т.д. 10 песчинок- куча, 3 песчинки –куча, 1 –куча. Итак, суть парадокса в том, что постепенные количественные изменения (убавление на 1 песчинку) не приводят к качественным изменениям.

 Парадокс «мэр города», состоит в следующем6 каждый мэр города живет или в своем городе, или вне его. Был издан приказ о выделении одного спец. Города, где бы жили только эти мэры, не живущие в своем городе. Где должен жить мэр этого спец. Города? Если он хочет жить в своем городе, то он не может этого сделать, т.к.. там живут только мэры, не живущие в своем городе; если же он не хочет жить в своем городе, то как и все мэры, не живущие в своих городах, он должен жить в отведенном городе, т.е. в своем. Итак, он не может жить ни в своем городе, ни вне его.

Парадокс «генерал и брадобрей» состоит: каждый солдат может сам себя брить или бриться у другого солдата. Генерал издал приказ о выделении одного спец. Солдата – брадобрея, у которого брились бы только е солдаты, которые себя не бреют. У кого должен бриться этот спец солдат –брадобрей? Итак, он не может брить себя.

Т.о, в логику входит категория времени, категория изменения: приходится рассматривать изменяющиеся объемы понятий. А рассматривание объема в процессе его изменения – это уже аспект диалектической логики.

Аргументация и ее роль в формировании убеждении. Доказательства, его структура, виды, правила и возможные ошибки

 

Познание отдельных предметов, их свойств происходит посредством форм чувственного познания (ощущений и восприятий). Мы видим, что этот дом еще не построен, ощущаем вкус горького лекарства и т.д. Эти истины не подлежат доказательству, они очевидны, однако во многих случаях, например, на лекции, научной работе, входе полемики и во многих других, нам приходится доказывать, обосновывать высказывания нами суждения.

Доказательство –это совокупность логических приемов обоснования истинности какого –либо суждения с помощью других истинных и связанных с ним суждений.

Доказательство связано с убеждением, но не тождественно ему: доказательства даны основываются на данных науки и общественно исторической практики, убеждения же могут быть основаны, например, на религиозной вере в догматы церкви, на предрассудках, на осведомленности людей в вопросах экономики и политики. Убедить еще не значит доказать.

Структура доказательства.

Тезис- это суждение, истинность которого надо доказать. Аргументы это те истинные суждения, которыми пользуются при доказательстве тезиса. Формат доказательства - называется способ логической связи между тезисами и аргументами.

Различаются несколько видов аргументов:

1.         удостоверенные единичные факты – такого рода аргументам относятся так называемый фактический материал, т.е. статические данные о населении территории государства, выполнение плана, свидетельские показания, подписи лица на документе, научные данные, научные факты. Роль фактов в обосновании выдвинутых положении, в том числе научных, очень велика.

 определение как аргументы доказательства. Определение понятий формируется в каждой науке. Правила и виды были рассмотрены в теме «понятия».