Навигация
Методы, основанные на применении производных высших порядков
2. Методы, основанные на применении производных высших порядков
До сих пор для численного интегрирования дифференциального уравнения первого порядка
![]() (1)
(1)
с начальным условием
![]() (2)
(2)
мы применяли формулы, в которых явно используется лишь первая производная ![]() искомого решения.
искомого решения.
Однако если использовать формулы, явно содержащие производные высших порядков от искомого решения, то можно указать методы, дающие более точный результат на данном промежутке без увеличения числа шагов.
Выведем соответствующие формулы, предполагая, что правая часть уравнения (1) дифференцируема достаточное число раз.
Пусть ![]() - значения искомого решения y=y(x) и, соответственно, значения его производных первого и второго порядков в точках
- значения искомого решения y=y(x) и, соответственно, значения его производных первого и второго порядков в точках ![]() . Располагая величины
. Располагая величины
![]()
в ряды по степеням h, находим:
![]()
![]()
![]()
Из полученных формул исключим члены, содержащие ![]()
![]() и
и ![]() .
.
Для этого вторую формулу умножим на ![]() , а третью – на
, а третью – на ![]() и сложим с первой. Будем иметь:
и сложим с первой. Будем иметь:
![]()
Таким образом, с точностью до ![]() имеем приближённую формулу
имеем приближённую формулу
![]() (3)
(3)
Можно показать, что остаточный член формулы (3) равен ![]() где
где ![]() Аналогично имеем:
Аналогично имеем:
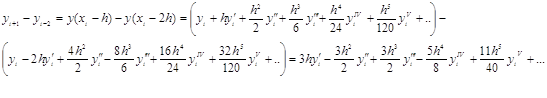 и
и
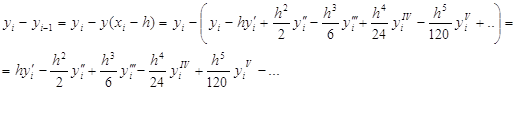
Отсюда

С другой стороны
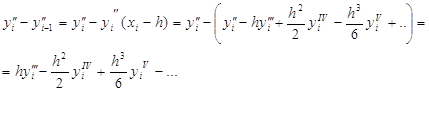
Поэтому
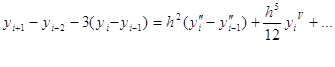
Таким образом, с точностью до h5 ![]() имеем приближённую формулу
имеем приближённую формулу
![]() (4)
(4)
Можно доказать, что остаточный член формулы (4) есть
![]()
где ![]()
К формулам (3) и (4) присоединим выражения для производных:
![]() (5)
(5)
![]() (6)
(6)
Процесс численного дифференцирования уравнения (1) при наличии начального условия (2), использющий формулы (3) и (4), происходит следующим образом. Каким-либо методом вычисляем три начальные строки (начальная таблица):

Из формулы (4) при i=2 получаем первое приближение для ![]() :
:
![]() (7)
(7)
и, пользуясь формулами (5) и (6), находим для соответствующих производных ![]() и
и ![]() их первые приближения:
их первые приближения:
![]() и
и ![]() .
.
Второе приближение для ![]() определяем при i=2 из формулы (3):
определяем при i=2 из формулы (3):
![]() (8)
(8)
После этого исправляем значения производных ![]() и
и ![]() , подсчитывая их вторые приближения:
, подсчитывая их вторые приближения:
![]() и
и ![]() .
.
Для контроля ещё раз вычисляем по формуле (3) третье приближение ![]() значения
значения ![]() , используя найденные значения
, используя найденные значения ![]() и
и ![]() .
.
Если шаг h выбран подходящим, то перещёт не даёт нового результата, и в этом случае можно положить ![]()
В противном случае следует уменьшить шаг. Аналогично находятся дальнейшие значения ![]() при i>3.
при i>3.
Для получения начальных значений ![]() и
и ![]() обычно используют метод последовательных приближений или метод Рунге-Кутта, после чего нужные производные
обычно используют метод последовательных приближений или метод Рунге-Кутта, после чего нужные производные ![]() и
и ![]() (i=0,1,2) определяются по формулам (5) и (6).
(i=0,1,2) определяются по формулам (5) и (6).
Можна также применить следующий приём: сначала, используя данное начальное значение ![]() , непосредственно вычисляем
, непосредственно вычисляем
![]() и
и ![]() .
.
Тем самым будет заполнена первая строка начальной таблицы .
Далее на основании формулы Тейлера приближённо получаем
![]()
и, следовательно, можно будит найти
![]() и
и ![]() .
.
Пользуясь этими данными, уточняем значение ![]() по формуле (3):
по формуле (3):
![]()
и затем перевычисляем значения ![]() и
и ![]() . Тем самым заполняем вторую строку начальной таблицы. Аналогично, исходя из второй строки, находим элементы
. Тем самым заполняем вторую строку начальной таблицы. Аналогично, исходя из второй строки, находим элементы ![]() ,
, ![]() и
и ![]() последней, третей строки начальной таблицы.
последней, третей строки начальной таблицы.
Отметим, что если пересчёты элементов строк дают значительные расхождения, то этот приём не является надёжным. В таком случае следует или уменьшить шаг h вычислений, или же обратиться к более точным методам.
В заключение приведём формулы, обеспечивающие более высокую степень точности, но требующие вычисления, кроме второй, ещё и третьей производной искомого решения. А именно, используя Формулу Тейлера и употребляя приём, аналогичный указанному выше, получаем формулы
![]() , (11)
, (11)
где
![]() , и
, и
![]() , (12)
, (12)
где ![]() .
.
Формула (11) употребляется для нахождения первого приближения ![]() ; формула (12) даёт уточнённое значение
; формула (12) даёт уточнённое значение ![]() . Само собой разумеется, что к последним двум формулам целесообразно прибегать тогда, когда форма дифференциального уравнения позволяет сравнительно просто находить вторую и третью производные от искомой функции y.
. Само собой разумеется, что к последним двум формулам целесообразно прибегать тогда, когда форма дифференциального уравнения позволяет сравнительно просто находить вторую и третью производные от искомой функции y.
Приложение
program proizw_w_p;
uses crt;
const epsilon=0.05;
type mas=array[1..100] of real;
nabl=array [1..3] of real;
var i:integer;
x,y,y1,y2:mas;
nabl1,nabl2,nabl3:nabl;
a,h:real;
n:integer;
function f(x, y:real):real;
begin
f:=sqr(x)-sqr(y);
end;
procedure metod(xi, yi, step: real; var rez:real);
var k1, k2, k3, k4:real;
begin
k1:=F(xi,yi);
k2:=F(xi+step/2,yi+k1*step/2);
k3:=F(xi+step/2,yi+k2*step/2);
k4:=F(xi+step,yi+k3*step);
rez:=yi+(step/6)*(k1+2*k2+2*k3+k4)
end;
procedure osn_metod(xi, yi, step:real;var yh22:real;var h:real);
var yh,yh2:real;
begin
repeat
metod(xi, yi,step, yh);
metod(xi, yi, step/2, yh2);
metod(xi, yh2, step/2, yh22);
if abs(yh-yh22)/15>epsilon then step:=h/2;
until abs(yh-yh22)/15<epsilon;
end;
procedure iteraziya(j:integer;xi,h:real);
begin
{первое приближение}
nabl1[1]:=y[j-3]+3*(y[j-1]-y[j-2])+sqr(h)*y2[j-1]-y2[j-2];
{производная первого приближения}
nabl1[2]:=sqr(xi)-sqr(nabl1[1]);
{вторая производная первого приближение}
nabl1[3]:=2*(xi-nabl1[1]*nabl1[2]);
{второе приближение}
nabl2[1]:=y[j-1]+(h/2)*(y1[j-1]+nabl1[2])+((sqr(h))/12)*(nabl1[3]-y2[j-1]);
{производная второго приближения}
nabl2[2]:=sqr(xi)-sqr(nabl2[1]);
{вторая производная второго приближения}
nabl2[3]:=2*(xi-nabl2[1]*nabl2[2]);
{третье приближение}
nabl3[1]:=y[j-1]+(h/2)*(y1[j-1]+nabl2[2])-(sqr(h)/12)*(nabl2[3]-y2[j-1]);
{производная третьего приближения}
nabl3[2]:=sqr(xi)-sqr(nabl3[1]);
{вторая производная третьего приближения}
nabl3[3]:=2*(xi-nabl2[1]*nabl2[2]);
end;
procedure solution(h:real);
begin
{==============Метод Рунге-Кута =================================}
a:=0;
i:=1;
y[1]:=1;
while i<4 do
begin
x[i+1]:=a+i*h;
osn_metod(x[i], y[i], h,y[i+1], h);
inc(i);
end;
{======Окончание метода Рунге-Кута =================================}
{============найдем первые и вторые производные===============}
for i:=1 to 3 do
begin
y1[i]:=sqr(x[i])-sqr(y[i]);
y2[i]:=2*(x[i]-y[i]*y1[i]);
end;
{=================================================================}
for i:=4 to n do
begin
iteraziya(i,x[i],h);
if abs(nabl3[1]-nabl2[1])<epsilon
then
begin
y[i]:=nabl3[1];
y1[i]:=nabl3[2];
y2[i]:=nabl3[3];
end
else
begin
h:=h/2;
if keypressed then halt;
solution(h);
end;
end;
end;
BEGIN
{=====================init==========================================}
clrscr;
write('введите количество значений, которые необходимо вычислить n= ');
readln(n);
h:=0.1;
{==================end of init=========================================}
for i:=1 to n do
begin
x[i]:=(i-1)*h;
end;
solution(h);
for i:=1 to n do
begin
write('y[',i,']= ',y[i],' y"[',i,']= ',y1[i],' y""[',i,']= ',y2[i]);
writeln;
end;
writeln('');
writeln('');
write('Press <enter> to exit....');
readln;
END.
Похожие работы
... значениями и корнями дифференциального уравнения Y(I), квадрат разности, а также производит их суммирование. Далее находится величина погрешности аппроксимации и все данные выводятся на экран. Общая программа решения дифференциального уравнения с последующей аппроксимацией результатов представлена на рис. 7 вместе с программой решения дифференциального уравнения, так как из нее получают значения ...
... в точке хк проводят вычисления ук с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений: | ук*-у(хк)|=1/3(yk*-yk), (2.5.9) где у(х)-точное решение дифференциального уравнения. Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y//=f(y/,y,x) c начальными условиями y/(x0)=y/0, y(x0)=y0, ...
... площадь, ограниченную заданными параболами Решение Точки пересечения по х: х = -1, х = 5. Площадь фигуры найдем из выражения Ответ: Задача 9 Найти общее решение дифференциального уравнения первого порядка Решение Разделим переменные Проинтегрируем Ответ: Задача 10 Найти частное решение линейного дифференциального уравнения первого порядка, ...
... = cos(aּπּt) и нулевых начальных условиях; 3. Выводы по работе №3 В процессе данной практической работы я изучил возможности математического пакета MathCad в среде Windows для решения дифференциальных уравнений N-го порядка, используемых в инженерных расчетах электротехнических систем. Были выполнены численные методы решения дифференциальных уравнений N-го порядка. Заданное ...
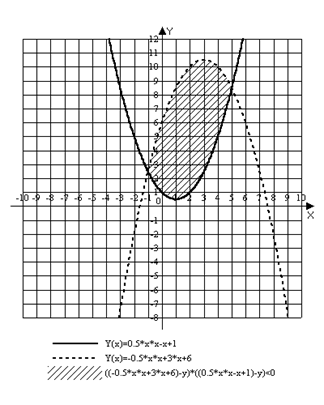
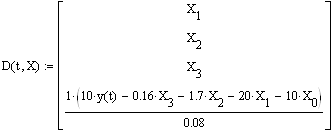


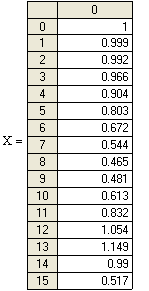

0 комментариев