Навигация
Решение произвольных систем линейных уравнений
Дисциплина: Высшая математика
Тема: Решение произвольных систем линейных уравнений
1. Решение произвольных систем линейных алгебраических уравнений
Выше рассмотрены решения квадратных невырожденных систем линейных алгебраических уравнений матричным методом и методом Крамера. Однако они не пригодны в тех случаях, когда квадратная система уравнений вырождена или когда система вообще не является квадратной.
В связи с этим перейдем к рассмотрению систем линейных алгебраических уравнений общего вида, когда ![]() :
:
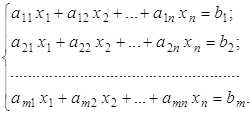
В данном случае матрица системы является прямоугольной, у нее нет определителя, и метод Крамера для решения системы не применим. Поэтому, прежде чем решать данную систему, рассмотрим две теоремы.
Теорема 1.1. Если ранг матрицы совместной системы линейных алгебраических уравнений равен числу неизвестных, то система имеет единственное решение.
Доказательство. Если ранг матрицы системы равен ![]() , то есть числу неизвестных, то строк у матрицы должно быть тоже
, то есть числу неизвестных, то строк у матрицы должно быть тоже ![]() . Следовательно,
. Следовательно, ![]() . Итак, по условию
. Итак, по условию ![]() . Но тогда любая, не входящая в базисный минор, строка расширенной матрицы является линейной комбинацией базисных строк и может быть обращена в ноль. То же самое происходит и с уравнением, соответствующим этой строке. Значит, исходная система эквивалентна
. Но тогда любая, не входящая в базисный минор, строка расширенной матрицы является линейной комбинацией базисных строк и может быть обращена в ноль. То же самое происходит и с уравнением, соответствующим этой строке. Значит, исходная система эквивалентна ![]() уравнениям с коэффициентами из базисного минора. Остальные
уравнениям с коэффициентами из базисного минора. Остальные ![]() уравнений из системы можно убрать, так как они является линейной комбинацией оставшихся. Получаем квадратную невырожденную систему линейных алгебраических уравнений с
уравнений из системы можно убрать, так как они является линейной комбинацией оставшихся. Получаем квадратную невырожденную систему линейных алгебраических уравнений с ![]() неизвестными, которая согласно правилу Крамера имеет единственное решение, что и требовалось доказать.
неизвестными, которая согласно правилу Крамера имеет единственное решение, что и требовалось доказать.
Теорема 1.2. Если ранг матрицы совместной системы линейных алгебраических уравнений меньше числа неизвестных, то система имеет бесконечное множество решений.
Доказательство. По условию система совместна и ![]() . Будем считать, что базисный минор
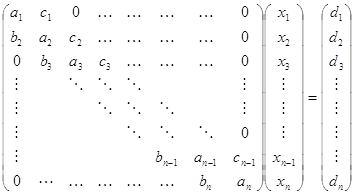
. Будем считать, что базисный минор ![]() расположен в левом верхнем углу расширенной матрицы системы
расположен в левом верхнем углу расширенной матрицы системы ![]() . Если это не так, то, переставляя строки и столбцы матрицы, можно получить нужный результат.
. Если это не так, то, переставляя строки и столбцы матрицы, можно получить нужный результат.
Минор будет иметь вид:
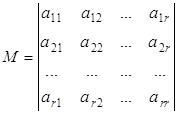 .
.
Так как любая строка матрицы ![]() , не вошедшая в базисный минор, является линейной комбинацией базисных, то ее можно обратить в ноль. Тогда, по аналогии с теоремой 1.1, из исходной системы можно убрать те уравнения, коэффициенты которых не попали в базисный минор. Следовательно, в ней останется
, не вошедшая в базисный минор, является линейной комбинацией базисных, то ее можно обратить в ноль. Тогда, по аналогии с теоремой 1.1, из исходной системы можно убрать те уравнения, коэффициенты которых не попали в базисный минор. Следовательно, в ней останется ![]() линейных алгебраических уравнений и исходную систему можно записать в виде:
линейных алгебраических уравнений и исходную систему можно записать в виде:
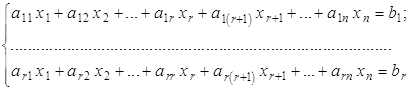
или
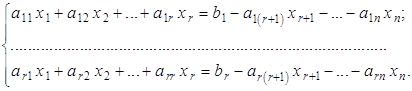
Придавая неизвестным ![]() произвольные значения
произвольные значения ![]() , получаем систему из
, получаем систему из ![]() уравнений с
уравнений с ![]() неизвестными:
неизвестными:
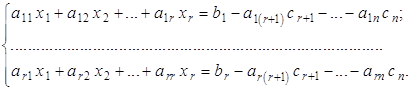
Данная система является квадратной, ее определитель ![]() , поэтому с помощью метода Крамера находим единственное решение
, поэтому с помощью метода Крамера находим единственное решение ![]() . Очевидно, задавая другие значения для
. Очевидно, задавая другие значения для ![]() , получим другие значения неизвестных
, получим другие значения неизвестных ![]() .
.
Так как числа ![]() могут быть заданы произвольно, то число решений системы бесконечно. Какое-то одно решение будет иметь вид:
могут быть заданы произвольно, то число решений системы бесконечно. Какое-то одно решение будет иметь вид:
 .
.
Неизвестные, коэффициенты при которых входят в базисный минор, называются базисными. Остальные неизвестные называются свободными.
Похожие работы
... , с помощью которых в последующем решение систем линейных уравнений станет намного проще, понятнее и быстрее. Цель моей работы заключается в том, чтобы изучить различные способы решения систем линейных уравнений для применения их на практике. Для достижения любой цели необходимо выполнить какие-то определенные задачи. Мне нужно выполнить следующие задачи: исследовать литературу по темам матриц, ...
... (19) где - матрица системы, - матрица правых частей, оценивается нормой: (20) Относительная погрешность оценивается по формуле: (21) где . 4. Итерационные методы решения систем линейных уравнений Рассмотрим систему линейных уравнений, которая плохо решается методами Гаусса. Перепишем систему уравнений в виде: ...
... i < NumFE; i++) for (DWORD j = 0; j < 10; j++) FE[i][j]--; printf(" r"); return true;}ПРИЛОЖЕНИЕ 2. Исходный текст программы, реализующей алгоритм компактного хранения и решения СЛАУ высокого порядка. #include "matrix.h" class RVector { private: Vector<double> Buffer; public: RVector(void) {} ~RVector() {} RVector(DWORD Size) { Buffer. ...
... Б (обязательное) ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ФАВТ РАЗРАБОТКА ПРОГРАММЫ ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ РУКОВОДСТВО ОПЕРАТОРА Лист утверждения ТПЖА.12203-01 34 01-ЛУ Листов 2 Разработал студент гр. СК-02 ____________ / А. И. ...
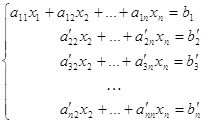
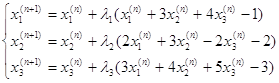

0 комментариев