Навигация
Если текущий символ - открывающая скобка, то помещаем ее в стек
3. Если текущий символ - открывающая скобка, то помещаем ее в стек.
4. Если текущий символ - закрывающая скобка, то извлекаем символы из стека в выходную строку до тех пор, пока не встретим в стеке открывающую скобку (т.е. символ с приоритетом, равным 1), которую следует просто уничтожить. Закрывающая скобка также уничтожается.
Если вся входная строка разобрана, а в стеке еще остаются знаки операций, извлекаем их из стека в выходную строку.
Согласно этим правилам создан модуль ”Unit3.cpp”, содержащий функцию преобразования строки в обратную польскую запись OPZ (блок 3 в блок-схеме алгоритма), алгоритм которой приведён в приложении. В данном модуле использованы также вспомогательные функции PUSH, PRIOR, DEL. Функция PUSH записывает в стек, на вершину которого указывает HEAD, символ a. Возвращает указатель на новую вершину стека. Функция PRIOR вычисляет приоритет текущего символа, естественно, лишь в том случае, если текущий символ – математическая операция. Функция DEL удаляет символ с веpшины стека. Возвpащает удаляемый символ. Изменяет указатель на веpшину стека.
Для работы с полученной обратной польской записью создана функция(блок 4), организованная в виде подключаемого модуля “Unit5.cpp”. Блок-схема данной функции приведена в приложении. На начальном этапе (блоки 1-13) в цикле анализируется строка, содержащая обратную польскую запись. Если символ ранее задекларирован (‘x’,’u’,’v’,’e’,’1’..’9’), то его значение заносится в текущий элемент массива th. На следующем этапе (блоки 14-29) осуществляется «обратный ход» польской нотации: анализируется каждый символ строки, и если этот символ ранее задекларирован, то его значение помещается в стек (блоки 15-17). В случае, если текущий символ – знак математической операции , то из стека извлекаются последние два элемента и с ними проводится указанная операция. Результат заносится на вершину стека. Стек в функции реализован в виде однонаправленного массива типа double. Функция возвращает первый элемент стека.
5. Описание программы
После проведённого обзора программных средств для разработки данного программного продукта, была выбрана среда Borland C++ Builder. Язык С++ хорошо зарекомендовал себя эффективностью, лаконичностью записи алгоритмов, логической стройностью программы, хорошей переносимостью. Программы, написанные на языке С++, сравнимы по скорости с программами, написанными на языке ассемблера; при этом они более наглядны и просты в сопровождении. Среда Borland C++ Builder является средством быстрой разработки windows-приложений, позволяющее создавать приложения на языке С++, используя среду разработки и библиотеку компонентов Delphi.
Готовая программа представляет собой исполняемый файл с именем “Adams3.exe”, реализованный в виде Widows-приложения в среде Borland C++ Builder. После запуска программы на рабочем окне появляется рабочее окно с заголовком «Решение систем дифференциальных уравнений» ( см. Приложение 3, рис.1). В активном окне можно выделить следующие области:
1) Область ввода исходных данных.
2) Окно вывода результатов.
3) Поле отображения графиков полученных функций, являющихся
решением заданной системы, и графиков истинного решения.
4) Основное меню.
1) Область исходных данных содержит поля, в которые требуется ввести начальные данные: систему дифференциальных уравнений; интервал, на котором требуется найти решение заданной системы; допустимую погрешность; условия Коши в начальной точке заданного интервала; количество шагов “сетки” и шаг вывода полученных значений искомых функций в узлах сетки.
В поля ”du/dx= “ и “dv/dx= “ вводятся дифференциальные уравнения, содержащие символы, ‘u’, ‘v’ ‘x’, ‘e’, ’1’..’9’, ’+’, ’-‘, ‘*’, ‘/’, ‘^’, ‘(‘, ‘)’. Здесь: символы ‘u’ и ‘v’ представляют собой искомые функции, символ ‘e’ является основанием натурального логарифма, символ ‘^’ обозначает операцию возведения в степень. Использование других символов нежелательно, так как они будут проигнорированы программой.
Поля с заглавием «интервал [a;b]» содержат начальную и конечную точку промежутка, на котором будет найдено решение заданной системы.
В поле «количество шагов сетки» требуется ввести целое число, равное количеству точек по оси OX на заданном интервале, в которых ищем значения функций u(x) и v(x).
Поле «шаг вывода» содержит целое число, определяющее частоту вывода на экран результатов из множества результатов во всех узлах заданной сетки.
Поля под общим названием «начальные условия» содержат условия Коши – значения искомых функций в начале заданного интервала [a,b].
Для корректной работы программы все поля должны быть заполнены. При запуске программы все вышеперечисленные поля уже содержат стандартную информацию для теста программы, которую можно изменять.
Пользователю предоставляется возможность выбора режима программы. При запуске программы метка возле надписи «Не использовать метод сгущающихся сеток» отсутствует, и программа, используя метод учащающихся сеток подберёт после первого нажатия кнопки «выполнит» оптимальное значение количества шагов для достижения заданной точности. После повторного нажатия кнопки «выполнить» будут произведены вычисления уже для рекомендуемого значения шага сетки. Если метка поставлена, то после нажатия кнопки «выполнить» будет решена задача Коши для заданного интервала, но заданная точность не будет достигнута. Данный режим позволяет вводить различные системы дифференциальных уравнений, отличных от стандартных тестовых, решением которых являются функции u(x)=2*x, v(x)=exp(x).
2) Все результаты, полученные в ходе работы программы, отображаются в отдельном окне (рис. 2). При желании, всю информацию из этого окна можно сохранить в отдельный файл.
3) Полученное решение в виде графиков искомых функций выводится в отдельное поле (рис. 2). Здесь отображаются также графики функций f(x)=2*x и f(x)=exp(x), являющихся точным решением для тестовых систем дифференциальных уравнений. Поле отображения графиков масштабируемо.
4) Основное меню содержит следующие пункты: «Файл» и «О программе» (рис. 3). В свою очередь пункт меню «Файл» содержит следующие подпункты: «новый», «открыть», «сохранить как…» и «выход».
При выборе пункта «новый» все поля и окна будут очищены. Поле отображения графиков будет также очищено.
Выбрав пункт «сохранить как…», вся информация из окна результатов будет сохранена в выбранный пользователем файл (по умолчанию с расширением .txt).
Выбор пункта «открыть» приводит к загрузке из уже сохранённого ранее файла системы дифференциальных уравнений.
Программа работает стабильно, не приводит к ошибкам.
Похожие работы
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
... , является важнейшей вспомогательной научно-технической задачей . Целью данной курсовой работы является разработка алгоритма решения систем линейных дифференциальных уравнений первого порядка пяти точечным методом прогноза и коррекции Адамса-Башфорта . 1. ПОСТАНОВКА ЗАДАЧИ Рассмотрим произвольную систему линейных дифференциальных уравнений первого порядка : ...
... в точке хк проводят вычисления ук с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений: | ук*-у(хк)|=1/3(yk*-yk), (2.5.9) где у(х)-точное решение дифференциального уравнения. Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y//=f(y/,y,x) c начальными условиями y/(x0)=y/0, y(x0)=y0, ...
... ____________________________ подпись " ______ " ________________ 2007 г. Студент ____________________________ Подпись " ____ " _________________ 2007 г. Содержание 1. Постановка задачи АНАЛИЗ Численные методы интегрирования (Исследование устойчивости САУ) Для заданной системы требуется определить: Передаточную функцию замкнутой системы, для случая ; Корни характеристического ...
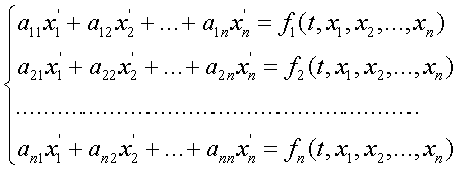
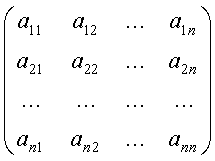
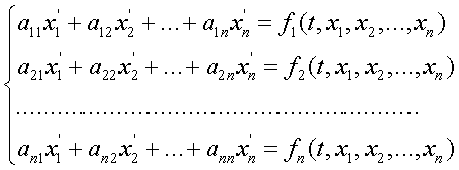
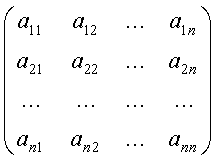
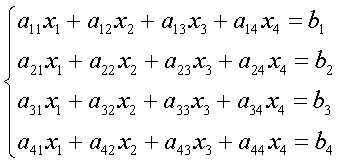
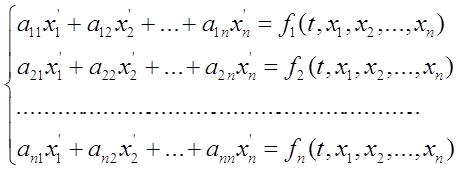

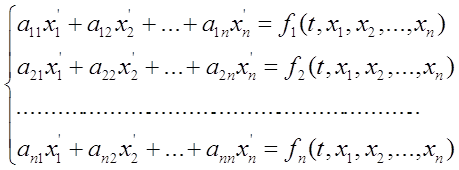
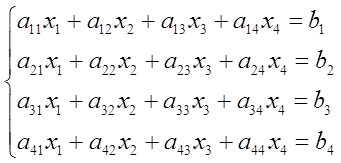
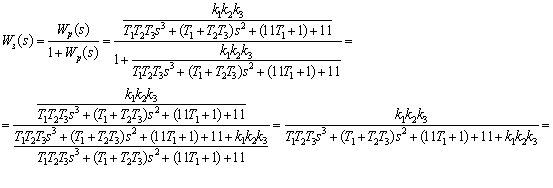
0 комментариев