Навигация
6. Анализ результатов
Результатом работы программы “Adams3.exe” является таблица значений полученного решения в узлах заданной сетки, значений точного решения и разность между точным и полученным решениями. Данную таблицу можно сохранить в текстовый файл с возможностью дальнейшего просмотра и редактирования.
В качестве тестовой задачи была решена задача Коши при помощи неявной схемы Адамса 3-го порядка на интервале [2,4] с начальными условиями ![]()
![]() :
:
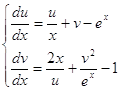 .
.
Точным решением данной системы являются функции:
![]()
Требовалось добиться решения системы дифференциальных уравнений с точностью до 0.0001.
Результат решения (выходной файл):
Входные данные:
du/dx= u/x+v-e^x;
dv/dx= 2*x/u+v^2/e^x-1;
Интервал: [2;4]
Допустимая погрешность: е=0,0001
Начальные условия:
u=4
v=7,389056098930650230
Количество шагов сетки: 320
Шаг вывода: 32
Результаты:
x | u(x) | точное | разн. | v(x) | точное | разн. |
2,000 4,0000 4,0000 0,0000 7,3891 7,3891 0,0000
2,200 4,4000 4,4000 0,0000 9,0250 9,0250 0,0000
2,400 4,8000 4,8000 0,0000 11,0232 11,0232 0,0000
2,600 5,2000 5,2000 0,0000 13,4637 13,4637 0,0000
2,800 5,6000 5,6000 0,0000 16,4446 16,4446 0,0000
3,000 6,0000 6,0000 0,0000 20,0855 20,0855 0,0000
3,200 6,4000 6,4000 0,0000 24,5325 24,5325 0,0000
3,400 6,8000 6,8000 0,0000 29,9641 29,9641 0,0000
3,600 7,2000 7,2000 0,0000 36,5982 36,5982 0,0000
3,800 7,6000 7,6000 0,0000 44,7012 44,7012 0,0000
4,000 8,0000 8,0000 0,0000 54,5981 54,5982 0,0000
Время выполнения: 0,015с
Как видно из полученного результата, точность в 0.0001 достигается уже при количестве шагов, равном 320. Время. Затраченное на расчёт таблицы значений на заданном интервале составляет всего 0.015 секунд, что практически не ощутимо. Увеличение шага сетки приведёт к повышению точности решения, однако это увеличит и время работы вычислительного процесса.
Заданная точность достигается за минимальное количество итерраций (1-3 итерации).
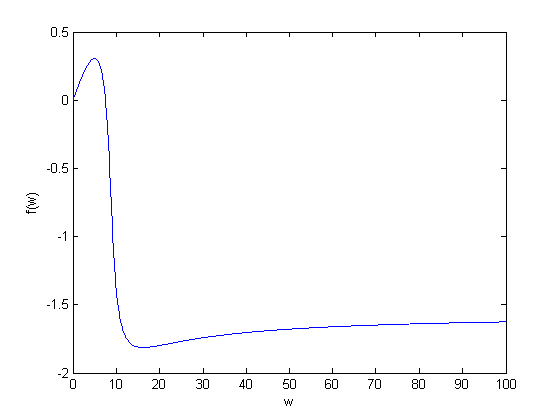
Ниже приведен график функций полученного и точного решений:
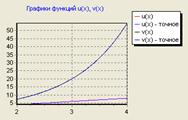
Рис. 5.1 График полученного и точного решения
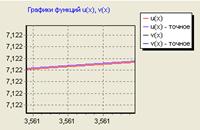
Рис. 5.2 График полученного и точного решения
Как видно из рисунков 5.1, 5.2, расхождение кривых наблюдается только при достаточно большом увеличении графика.
Предложенная задача Коши была также решена в математическом пакете “ Mathcad 11” двумя методами: методом Рунге-Кутта 5-го порядка и методом Рунге-Кутта с непостоянным шагом. Реализация решения системы дифференциальных уравнений в “ Mathcad 11” и таблицы результатов приведены ниже:
Реализация решения задачи Коши методом Рунге-Кутта 5-го порядка:
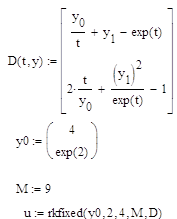
Таблица 5.1 – Результаты решения задачи Коши методом Рунге-Кутта 5-го порядка.
| x | u(x) | v(x) | x | u(x) | v(x) | |
| 2 | 4 | 7,3890561 | 3,1 | 6,2 | 22,19795 | |
| 2,02 | 4,04 | 7,5383249 | 3,12 | 6,24 | 22,64638 | |
| 2,04 | 4,08 | 7,6906092 | 3,14 | 6,28 | 23,10387 | |
| 2,06 | 4,12 | 7,8459698 | 3,16 | 6,32 | 23,5706 | |
| 2,08 | 4,16 | 8,0044689 | 3,18 | 6,36 | 24,04675 | |
| 2,1 | 4,2 | 8,1661699 | 3,2 | 6,4 | 24,53253 | |
| 2,12 | 4,24 | 8,3311375 | 3,22 | 6,44 | 25,02812 | |
| 2,14 | 4,28 | 8,4994376 | 3,24 | 6,48 | 25,53372 | |
| 2,16 | 4,32 | 8,6711376 | 3,26 | 6,52 | 26,04954 | |
| 2,18 | 4,36 | 8,8463062 | 3,28 | 6,56 | 26,57577 | |
| 2,2 | 4,4 | 9,0250135 | 3,3 | 6,6 | 27,11264 | |
| 2,22 | 4,44 | 9,2073308 | 3,32 | 6,64 | 27,66035 | |
| 2,24 | 4,48 | 9,3933313 | 3,34 | 6,68 | 28,21913 | |
| 2,26 | 4,52 | 9,5830891 | 3,36 | 6,72 | 28,78919 | |
| 2,28 | 4,56 | 9,7766804 | 3,38 | 6,76 | 29,37077 | |
| 2,3 | 4,6 | 9,9741824 | 3,4 | 6,8 | 29,9641 | |
| 2,32 | 4,64 | 10,175674 | 3,42 | 6,84 | 30,56941 | |
| 2,34 | 4,68 | 10,381237 | 3,44 | 6,879999 | 31,18696 | |
| 2,36 | 4,72 | 10,590951 | 3,46 | 6,919999 | 31,81698 | |
| 2,38 | 4,76 | 10,804903 | 3,48 | 6,959999 | 32,45972 | |
| 2,4 | 4,8 | 11,023176 | 3,5 | 6,999999 | 33,11545 | |
| 2,42 | 4,84 | 11,245859 | 3,52 | 7,039999 | 33,78443 | |
| 2,44 | 4,88 | 11,473041 | 3,54 | 7,079999 | 34,46692 | |
| 2,46 | 4,92 | 11,704811 | 3,56 | 7,119999 | 35,1632 | |
| 2,48 | 4,96 | 11,941264 | 3,58 | 7,159999 | 35,87354 | |
| 2,5 | 4,9999999 | 12,182494 | 3,6 | 7,199999 | 36,59823 | |
| 2,52 | 5,0399999 | 12,428597 | 3,62 | 7,239999 | 37,33757 | |
| 2,54 | 5,0799999 | 12,679671 | 3,64 | 7,279999 | 38,09184 | |
| 2,56 | 5,1199999 | 12,935817 | 3,66 | 7,319999 | 38,86134 | |
| 2,58 | 5,1599999 | 13,197138 | 3,68 | 7,359999 | 39,64639 | |
| 2,6 | 5,1999999 | 13,463738 | 3,7 | 7,399999 | 40,4473 | |
| 2,62 | 5,2399999 | 13,735723 | 3,72 | 7,439999 | 41,26439 | |
| 2,64 | 5,2799999 | 14,013204 | 3,74 | 7,479999 | 42,09799 | |
| 2,66 | 5,3199999 | 14,296289 | 3,76 | 7,519999 | 42,94842 | |
| 2,68 | 5,3599999 | 14,585093 | 3,78 | 7,559999 | 43,81604 | |
| 2,7 | 5,3999999 | 14,879732 | 3,8 | 7,599999 | 44,70118 | |
| 2,72 | 5,4399999 | 15,180322 | 3,82 | 7,639999 | 45,60421 | |
| 2,74 | 5,4799999 | 15,486985 | 3,84 | 7,679999 | 46,52547 | |
| 2,76 | 5,5199999 | 15,799843 | 3,86 | 7,719999 | 47,46535 | |
| 2,78 | 5,5599999 | 16,119021 | 3,88 | 7,759999 | 48,42421 | |
| 2,8 | 5,5999999 | 16,444647 | 3,9 | 7,799999 | 49,40245 | |
| 2,82 | 5,6399999 | 16,776851 | 3,92 | 7,839999 | 50,40044 | |
| 2,84 | 5,6799999 | 17,115765 | 3,94 | 7,879999 | 51,4186 | |
| 2,86 | 5,7199999 | 17,461527 | 3,96 | 7,919999 | 52,45732 | |
| 2,88 | 5,7599999 | 17,814273 | 3,98 | 7,959998 | 53,51703 | |
| 2,9 | 5,7999998 | 18,174145 | 4 | 7,999998 | 54,59815 | |
| 2,92 | 5,8399998 | 18,541287 | ||||
| 2,94 | 5,8799998 | 18,915846 | ||||
| 2,96 | 5,9199998 | 19,297972 | ||||
| 2,98 | 5,9599998 | 19,687816 | ||||
| 3 | 5,9999998 | 20,085537 | ||||
| 3,02 | 6,0399998 | 20,491291 | ||||
| 3,04 | 6,0799998 | 20,905243 | ||||
| 3,06 | 6,1199998 | 21,327557 | ||||
| 3,08 | 6,1599998 | 21,758402 |
Реализация решения задачи Коши методом Рунге-Кутта с непостоянным шагом:
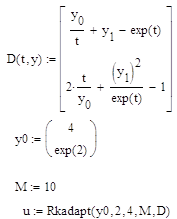
Таблица 5.2 – Результаты решения задачи Коши методом Рунге-Кутта с непостоянным шагом.
| X | u(x) | v(x) |
| 2 | 4 | 7,389056099 |
| 2,2 | 4,4 | 9,025013486 |
| 2,4 | 4,8 | 11,02317634 |
| 2,6 | 5,2 | 13,46373796 |
| 2,8 | 5,6 | 16,44464663 |
| 3 | 6 | 20,08553669 |
| 3,2 | 6,4 | 24,53252981 |
| 3,4 | 6,8 | 29,96409944 |
| 3,6 | 7,2 | 36,59823348 |
| 3,8 | 7,6 | 44,701183 |
| 4 | 8 | 54,59814775 |
Как видно из полученных таблиц результатов, точность решения в 0.0001 при решении методом Рунге-Кутта с непостоянным шагом достигается всего за 10 шагов, в то время, когда для достижения этой же точности при решении методом Рунге-Кутта 5-го порядка с постоянным шагом требуется около 100 шагов.
Сравнивая полученные результаты с результатами работы программы “Adams3.exe”, приходим к выводу, что неявная схема Адамса третьего порядка достаточно эффективна при численном решении задачи Коши (быстрота, высокая точность решения), однако по своим характеристикам она уступает более совершенным методам, применяющимися в различных математических пакетах.
Заключение
Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности.
Готовый программный продукт может найти широкое применение при решении многих прикладных технических программ, а в частности, эффективно использование применённой схемы Адамса 3-го порядка для решения так называемых “жёстких” систем дифференциальных уравнний, для которых существует лишь численное решение.
Данная программа решает заданную пользователем систему дифференциальных уравнений с указанной точностью за минимальный промежуток времени. При этом пользователю предоставляется возможность визуально оценить неточность решения, сравнивая графики полученного и точного решений.
К достоинствам программы можно отнести также удобный пользовательский интерфейс, возможность ввода пользовательских систем дифференциальных уравнений, а также высокая стабильность работы. Однако имеются и некоторые недостатки. К недостаткам программы можно отнести: критичность к вводимым пользователем функций, отсутсвие обработки исключительных событий. Это, естественно, ограничивает возможности программы.
Литература
1. Архангельский А.Я. Программирование в С++ Builder 6. – М.: ЗАО “Издательство БИНОМ”, 2002. – 360 с.
2. Калиткин Н.Н. Численные методы. ¾ М.: Наука, 1978. ¾ 512 с.
3. Самарский А.А., Гулин А.В. Численные методы. ¾ М.: Наука, 1989. – 432с.
4. Синицын А.К., Навроцкий А.А. Алгоритмы вычислительной математики. - Мн.: БГУИР,2002. – 80 с: ил.
5. Синицин А.К. Программирование алгоритмов в среде Builder C++. –Мн.: БГУИР, 2004. – 90 с.: ил.
6. Страуструп Бьерн. Язык программирования C++. –М.: ЗАО “Издательство БИНОМ”, 2002. – 1099c.:ил.
7. Шилд Г. Программирование на Borland C++ для профессионалов— М.:ООО “попурри” ,1999. – 800c.:ил.
Приложения
Приложение 1
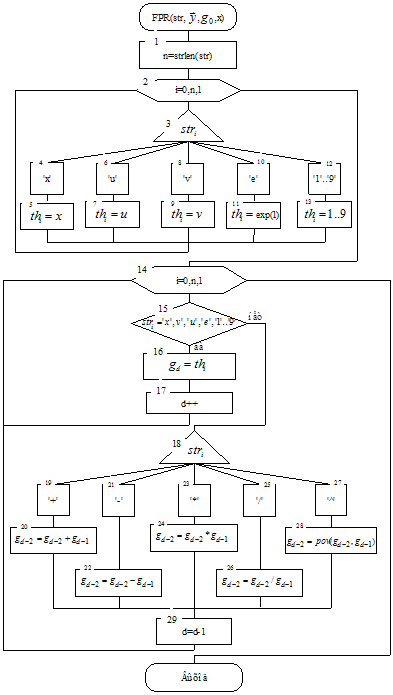
Блок-схема алгоритма
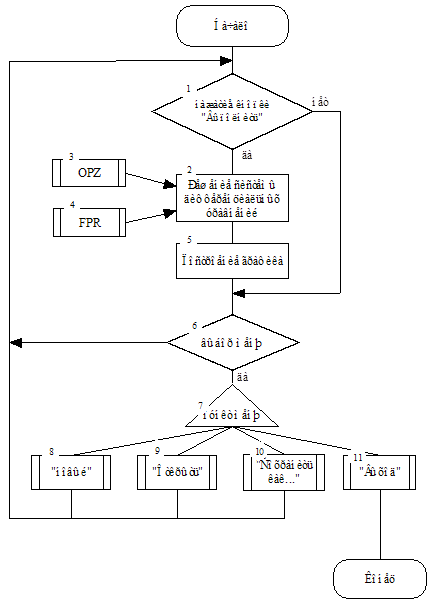
Блок-схема решения задачи Коши неявной схемой Адамса 3-го порядка.
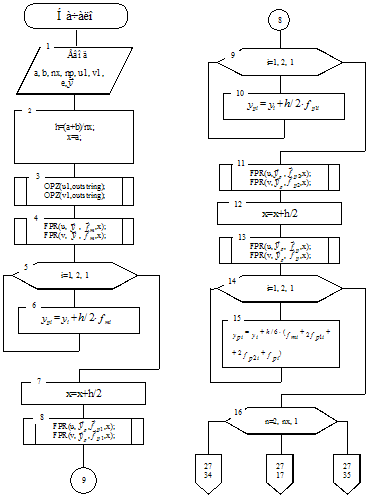
Блок-схема алгоритма преобразования строки в обратную польскую запись:
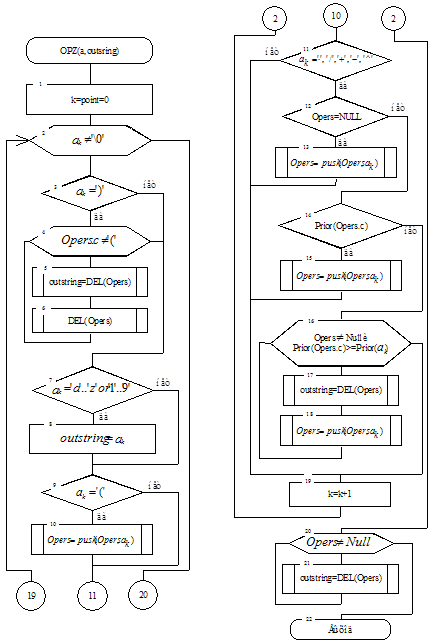
Блок-схема вычисления функций:
Приложение 2
Листинг программы
Главная программа (Unit1.cpp):
//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include "Unit1.h"
#include "Unit2.h"
#include "math.h"
#include "stdio.h"
#include "Unit3.h"
#include "Unit5.h"
#include "fstream.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
char *opz(char *); // ф-ия преобразования в обратную польскую запись;
double fpr(char *str,double u, double v,double x); // обратный ход польской
int p=1,s=1,j=1,o=0; // записи;
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{
}
//---------------------------------------------------------------------------
void __fastcall TForm1::N5Click(TObject *Sender)
{
Form1->Close();
}
//---------------------------------------------------------------------------
void __fastcall TForm1::Button3Click(TObject *Sender)
{
Form1->Close();
}
//---------------------------------------------------------------------------
void __fastcall TForm1::N7Click(TObject *Sender)
{
Form2->Show();
}
//---------------------------------------------------------------------------
void __fastcall TForm1::N2Click(TObject *Sender) // очистка формы
{
Edit1->Clear();
Edit2->Clear();
Edit3->Clear();
Edit4->Clear();
Edit5->Clear();
Edit6->Clear();
Edit7->Clear();
Edit8->Clear();
Edit9->Clear();
Memo1->Clear();
Series1->Clear();
Series2->Clear();
Series3->Clear();
Series4->Clear();
}
//---------------------------------------------------------------------------
void __fastcall TForm1::FormCreate(TObject *Sender)
{
Edit1->Text="10";
Edit2->Text="1";
Edit3->Text="2";
Edit4->Text="4";
Edit5->Text="0,0001";
Edit6->Text="4";
Edit7->Text=FloatToStrF(exp(2),ffFixed,20,18);
Memo1->Text="результаты программы";
Button1->Show();
}
//---------------------------------------------------------------------------
void __fastcall TForm1::Button1Click(TObject *Sender) //обработка события нажатия кнопки «выполнить»
{
//---------------------------------------------------------------------------
int nx,np,k,i,n;
double a,b,e,h,d,de,z,x;
double y[2],yp[2],f[2],fm[2],fp[2],fp1[2],fp2[2];
unsigned long int time=GetTickCount();
unsigned long int time1=0;
a=StrToFloat(Edit3->Text);
b=StrToFloat(Edit4->Text);
e=StrToFloat(Edit5->Text);
nx=StrToInt(Edit1->Text);
np=StrToInt(Edit2->Text);
Memo1->Clear();
Memo1->Lines->Add("Входные данные:");
Memo1->Lines->Add("");
Memo1->Lines->Add("du/dx="+Edit8->Text+";");
Memo1->Lines->Add("dv/dx="+Edit9->Text+";");
Memo1->Lines->Add("Интервал: ["+Edit3->Text+";"+Edit4->Text+"]");
Memo1->Lines->Add("Допустимая погрешность: е="+Edit5->Text);
Memo1->Lines->Add("Начальные условия:");
Memo1->Lines->Add("u="+Edit6->Text);
Memo1->Lines->Add("v="+Edit7->Text);
Memo1->Lines->Add("Количество шагов сетки: "+Edit1->Text);
Memo1->Lines->Add("Шаг вывода: "+Edit2->Text);
Memo1->Lines->Add("");
Memo1->Lines->Add("");
char *u1 =(char *)malloc(strlen(Edit8->Text.c_str())+1);
char *v1 =(char *)malloc(strlen(Edit9->Text.c_str())+1);
strcpy(u1,Edit8->Text.c_str());
strcpy(v1,Edit9->Text.c_str());
char *u =(char *)malloc(strlen(u1)+1); //динамическое выделение памяти
char *v =(char *)malloc(strlen(v1)+1);
strcpy(u,opz(&(u1[0]))); // преобразование в обратную польскую запись
strcpy(v,opz(&(v1[0])));
do {
h=(b-a)/nx;
x=a;
y[0]=StrToFloat(Edit6->Text);
y[1]=StrToFloat(Edit7->Text);
if(np!=0&&s==0){
Memo1->Lines->Add("Результаты:");
Memo1->Lines->Add(" x | u(x) | точное | разн. | v(x) | точное | разн. | ");
Memo1->Lines->Add("-----------------------------------------------------");
Memo1->Lines->Add(FloatToStrF(x,ffFixed,5,3)+" "+FloatToStrF(y[0],ffFixed,8,4)+" "+FloatToStrF(2*x,ffFixed,8,4)+" "+FloatToStrF(y[0]-2*x,ffFixed,8,4)+" "+FloatToStrF(y[1],ffFixed,8,4)+" "+FloatToStrF(exp(x),ffFixed,8,4)+" "+FloatToStrF(y[1]-exp(x),ffFixed,8,4));
}
Series1->Clear();
Series2->Clear();
Series3->Clear();
Series4->Clear();
Series1->AddXY(x,y[0]);
Series2->AddXY(x,2*x);
Series3->AddXY(x,y[1]);
Series4->AddXY(x,exp(x));
fm[0]=fpr(u,y[0],y[1],x);
fm[1]=fpr(v,y[0],y[1],x);
for(i=0;i<2;i++)
{
yp[i]=y[i]+h/2*fm[i];
}
x=x+h/2;
fp1[0]=fpr(u,yp[0],yp[1],x);
fp1[1]=fpr(v,yp[0],yp[1],x);
for(i=0;i<2;i++)
{
yp[i]=y[i]+h/2*fp1[i];
}
fp2[0]=fpr(u,yp[0],yp[1],x);
fp2[1]=fpr(v,yp[0],yp[1],x);
for(i=0;i<2;i++)
{
yp[i]=y[i]+h*fp2[i];
}
x=x+h/2;
fp[0]=fpr(u,yp[0],yp[1],x);
fp[1]=fpr(v,yp[0],yp[1],x);
for(i=0;i<2;i++)
{
yp[i]=y[i]+h*(fm[i]+2*fp1[i]+2*fp2[i]+fp[i])/6;
}
fp[0]=fpr(u,yp[0],yp[1],x);
fp[1]=fpr(v,yp[0],yp[1],x);
for(n=2;n<=nx;n++)
{
for(i=0;i<2;i++)
{
y[i]=yp[i]+h*(1.5*fp[i]-0.5*fm[i]);
};
x=x+h;
f[0]=fpr(u,y[0],y[1],x);
f[1]=fpr(v,y[0],y[1],x);
k=0;
do
{
k=k+1;
de=0;
for(i=0;i<2;i++)
{
z=yp[i]+h*(5*f[i]+8*fp[i]-fm[i])/12;
d=fabs(z-y[i]);
y[i]=z;
if(d>de) de=d;
};
f[0]=fpr(u,y[0],y[1],x);
f[1]=fpr(v,y[0],y[1],x);
} while(de>e);
for(i=0;i<2;i++)
{
yp[i]=y[i];
fm[i]=fp[i];
fp[i]=f[i];
}
Series1->AddXY(x,y[0]); //вывод графиков функций
Series2->AddXY(x,2*x);
Series3->AddXY(x,y[1]);
Series4->AddXY(x,exp(x));
if((fmod(n,np)==0)&&s==0) { //вывод результатов
Memo1->Lines->Add(FloatToStrF(x,ffFixed,5,3)+" "+FloatToStrF(y[0],ffFixed,8,4)+" "+FloatToStrF(2*x,ffFixed,8,4)+" "+FloatToStrF(y[0]-2*x,ffFixed,8,4)+" "+FloatToStrF(y[1],ffFixed,8,4)+" "+FloatToStrF(exp(x),ffFixed,8,4)+" "+FloatToStrF(y[1]-exp(x),ffFixed,8,4));
p=1;
o=1;
}
else o=0;
}
nx=nx*2;
np=np*2;
time1=GetTickCount();
if (o==1) {
Memo1->Lines->Add("------------------------------------------------------");
Memo1->Lines->Add("Время выполнения:"+FloatToStrF((time1-time)/1000.,ffFixed,6,3)+"мс");
}
if(CheckBox1->Checked) y[1]=exp(x);
} while(fabs(y[1]-exp(x))>e);
j++;
s=1;
if(p==1&&(fmod(j,2)==0))
{
Memo1->Lines->Add("Рекомендуемое значение шага сетки :"+FloatToStrF(nx/2,ffFixed,6,0));
Edit1->Text=FloatToStrF(nx/2,ffFixed,5,0);
Edit2->Text=FloatToStrF(np/2,ffFixed,5,0);
s=0;
p=0;
}
free(u); // освобождение памяти
free(v);
free(u1);
free(v1);
}
//---------------------------------------------------------------------------
void __fastcall TForm1::N4Click(TObject *Sender) //Сохранение в файл
{
SaveDialog1->Title="Save File";
if (SaveDialog1->Execute())
{
Memo1->Lines->SaveToFile(SaveDialog1->FileName);
}
}
//---------------------------------------------------------------------------
void __fastcall TForm1::N3Click(TObject *Sender) // Загрузка из файла функций
{
if(OpenDialog1->Execute())
{
FILE *fl;
fl=fopen(OpenDialog1->FileName.c_str(),"r");
char ch=getc(fl);
char str[30];
str[0]='\0';
int k=0;
while (ch!=EOF)
{
if(ch=='=') { k++;
while (ch!=';'){ ch=getc(fl);
int n=strlen(str);
str[n]=ch;
str[n+1]='\0';
}
switch (k)
{
case 1: Edit8->Text=str; str[0]='\0'; break;
case 2: Edit9->Text=str; break;
}
}
ch=getc(fl);
}
fclose(fl);
}
}
//---------------------------------------------------------------------------
Модуль преобразования строки в обратную польскую запись (Unit3.cpp):
//---------------------------------------------------------------------------
#pragma hdrstop
#include "Unit3.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
struct st {
char c;struct st *next;
};
struct st *push(struct st *,char);
char DEL(struct st **);
int PRIOR(char);
char* opz(char *a)
{
struct st *OPERS=NULL;
char *outstring= new char [30]; // динамическое выделение памяти
int k,point;
k=point=0;
while((*(a+k)!='\0')&&(*(a+k)!='=')){
if(*(a+k)==')'){
while((OPERS->c)!='(')
outstring[point++]=DEL(&OPERS);
DEL(&OPERS);
}
if((*(a+k)>='a'&&(*(a+k))<='z')||(*(a+k)>='1'&&(*(a+k))<='9'))
outstring[point++]=*(a+k);
if(a[k]=='(')
OPERS=push(OPERS,'(');
if(*(a+k)=='+'||*(a+k)=='-'||*(a+k)=='/'||*(a+k)=='*'||*(a+k)=='^'){
if(OPERS==NULL)
OPERS=push(OPERS,*(a+k));
else
if(!PRIOR(OPERS->c))
OPERS=push(OPERS,*(a+k));
else{
while((OPERS!=NULL)&&(PRIOR(OPERS->c)>=PRIOR(*(a+k))))
outstring[point++]=DEL(&OPERS);
OPERS=push(OPERS,*(a+k));
}
}
k++;
}
while(OPERS!=NULL)
outstring[point++]=DEL(&OPERS);
outstring[point]='\0';
return outstring;
}
struct st *push(struct st *HEAD,char a) /* Функция записывает в стек,на веpшину котоpого указывает HEAD,символ a.
Возвpащает указатель на новую веpшину стека*/
{
struct st *PTR;
PTR=new st ();
PTR->c=a;
PTR->next=HEAD;
return PTR;
}
char DEL(struct st **HEAD){ /* функция удаляет символ с веpшины стека. Возвpащает удаляемый символ.
Изменяет указатель на веpшину стека*/
struct st *PTR;
char a;
if(*HEAD==NULL)
return '\0';
PTR=*HEAD;
a=PTR->c;
*HEAD=PTR->next;
free(PTR);
return a;
}
int PRIOR(char a) //функция возвpащает пpиоpитет аpифметической опеpации
{
switch(a){
case '^':
return 4;
case '*':
case '/':
return 3;
case '-':
case '+':
return 2;
case '(':
return 1;
}
}
Модуль расчёта функции, записанной в постфиксной форме (Unit5.cpp):
//---------------------------------------------------------------------------
#pragma hdrstop
#include "Unit5.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#include<conio.h>
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
#include<string.h>
double fpr(char *str,double u, double v,double x)
{
int n,i,d=0;
double th[30],g[30];
n=strlen(str) ;
for (i=0;i<n;i++)
{
switch (*(str+i))
{
case 'x': *(th+i)=x; break;
case 'u': *(th+i)=u; break;
case 'v': *(th+i)=v; break;
case 'e': *(th+i)=exp(1); break;
case '1':
case '2':
case '3':
case '4':
case '5':
case '6':
case '7':
case '8':
case '9':
case '0': char p[1]; p[0]=str[i]; th[i]=atoi(p); break;
}
}
for(i=0;i<n;i++)
{
if(*(str+i)=='x'||*(str+i)=='v'||*(str+i)=='u'||*(str+i)=='e'||*(str+i)=='1'||*(str+i)=='2'||*(str+i)=='3'||*(str+i)=='4'||*(str+i)=='5'||*(str+i)=='6'||*(str+i)=='7'||*(str+i)=='8'||*(str+i)=='9')
{
*(g+d)=*(th+i);
d++;
}
else {
switch (*(str+i))
{
case '-': *(g+d-2)=*(g+d-2)-*(g+d-1); break;
case '+': *(g+d-2)=*(g+d-2)+*(g+d-1); break;
case '/': *(g+d-2)=*(g+d-2)/(*(g+d-1)); break;
case '*': *(g+d-2)=*(g+d-2)*(*(g+d-1)); break;
case '^': *(g+d-2)=pow(*(g+d-2),*(g+d-1)); break;
};
d--;
}
}
return *g;
}
Приложение 3
Рис 1. Общий вид программы
Рис 2. Организация решения системы
Рис 3. Организация меню
Похожие работы
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
... , является важнейшей вспомогательной научно-технической задачей . Целью данной курсовой работы является разработка алгоритма решения систем линейных дифференциальных уравнений первого порядка пяти точечным методом прогноза и коррекции Адамса-Башфорта . 1. ПОСТАНОВКА ЗАДАЧИ Рассмотрим произвольную систему линейных дифференциальных уравнений первого порядка : ...
... в точке хк проводят вычисления ук с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений: | ук*-у(хк)|=1/3(yk*-yk), (2.5.9) где у(х)-точное решение дифференциального уравнения. Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y//=f(y/,y,x) c начальными условиями y/(x0)=y/0, y(x0)=y0, ...
... ____________________________ подпись " ______ " ________________ 2007 г. Студент ____________________________ Подпись " ____ " _________________ 2007 г. Содержание 1. Постановка задачи АНАЛИЗ Численные методы интегрирования (Исследование устойчивости САУ) Для заданной системы требуется определить: Передаточную функцию замкнутой системы, для случая ; Корни характеристического ...
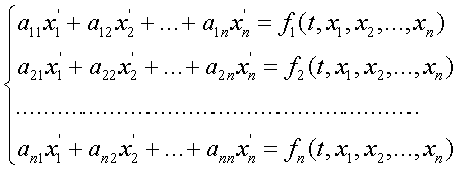
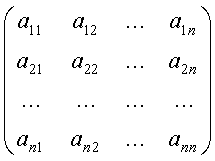
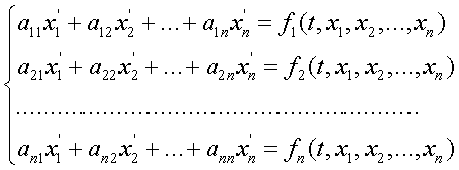
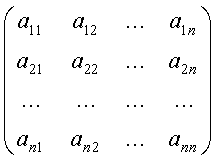
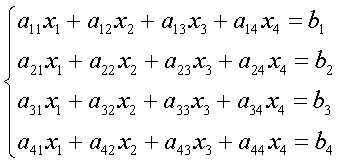
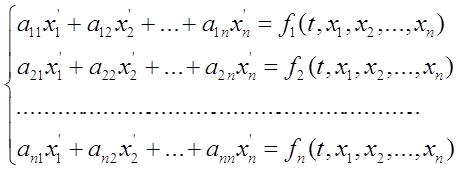

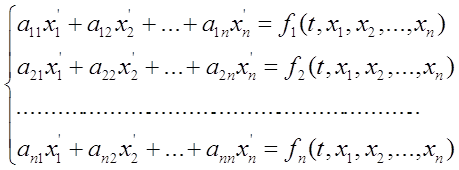
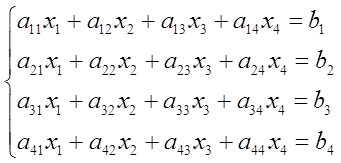
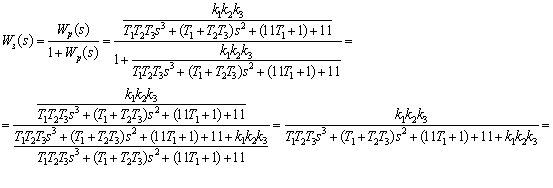
0 комментариев