Навигация
1.2 Компактна схема Гауса
Якщо обчислення по схемі єдиного ділення ведуться за допомогою обчислювальних машин, то багато часу затрачається на запис проміжних результатів. Компактна схема Гауса дає економний спосіб запису. Розглянемо порядок складення схеми для системи:
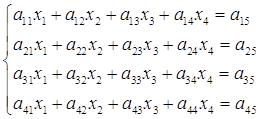
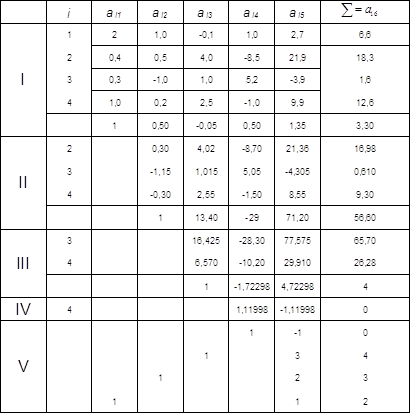
Всі результати обчислення будемо записувати в одну таблицю (Таблиця 1)
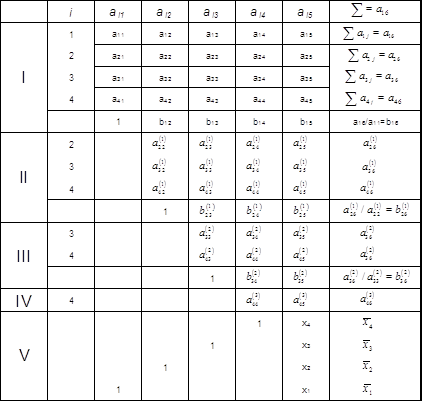
Компактна схема Гауса. Таблиця 1.
Порядок заповнення таблиці.
Прямий хід.
1) Записуємо коефіцієнти даної системи в чотирьох рядках і п’яти стовпцях розділу І таблиці 1.
2) Додаємо всі коефіцієнти по рядку і записуємо суму в стовпчик 
(стовпчик контролю), наприклад 
.
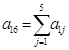3) Ділимо всі числа, які стоять в першому рядку, на 
і результати 
записуємо в п’ятому рядку розділу І.
4) Обчислюємо 
і робимо перевірку. Якщо обчислення ведуться з постійним числом знаків після коми, то числа 
і не повинні відрізнятися не більше ніж на одиницю останнього розряду. В іншому випадку потрібно перевірити дії пункту 3).
5) По формулам (2.4) обчислюємо коефіцієнти:
Результати записуємо в перші три рядки розділу ІІ.
6) Робимо перевірку. Сума елементів кожного рядка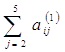 
не повинна відрізнятися від 
більше чим на одиницю останнього розряду (якщо всі обчислення ведуться з постійним числом знаків після коми).
7) Ділимо всі елементи першого рядка розділу ІІ на 
і результати записуємо в четвертому рядку розділу ІІ.
8) Робимо перевірку, як в пункті 4).
9) За формулами (2.7) обчислюємо 
Результати записуємо в перші два рядки розділу ІІІ.
10) Робимо перевірку, як в пункті 6).
11) Ділимо елементи першого рядка розділу ІІІ на 
і знаходимо числа 
. Всі результати записуємо в третьому рядку розділу ІІІ.
12) Робимо перевірку.
13) Обчислюємо 
. Результати записуємо в розділі IV.
Обернений хід.
1) В розділі V записуємо одиниці, як це показано в таблиці 1.
2) Обчислюємо 
3) Для обчислення значення 
використовуємо лише рядки розділів І, ІІ, ІІІ, що містять одиниці, починаючи з останньої. Так, для обчислення 
помножимо 
на 
і результати віднімаємо з 
. При цьому одиниці, розставлені в розділі V, допомагають знаходити для 
відповідні коефіцієнти в помічених рядках.
Таким чином,
.
4) Обчислюємо 
, для чого використовуємо елементи поміченого рядка розділу ІІ:
5) Обчислюємо 
, для чого використовуємо елементи поміченого рядка розділу І: 
Аналогічно проводиться обернений хід в контрольній системі. Розв’язок цієї системи повинен відрізнятися від розв’язку даної системи на 1 (з точністю до одиниці останнього розряду): 
Цей контроль здійснюється за допомогою стовпця 
Таким же чином реалізується компактна схема Гауса для систем з іншим числом невідомих. Компактна схема Гауса особливо потрібна при одночасному розв’язанні декількох систем, які відрізняються лише стовпцями вільних членів, що має місце, наприклад, при обчисленні елементів оберненої матриці.
Компактна схема Гауса для системи (2.12). Таблиця 2.
Похожие работы
... ’язок де С1, С2 - довільні сталі. Загальний розв’язок системи лінійних алгебраїчних рівнянь подається не в одному й тому самому вигляді. 2. Метод Гауса Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь полягає в послідовному виключенні змінних і перетворенні системи рівнянь (1) до трикутного вигляду (2) Припустимо, що в системі (1) коефіцієнт . Якщо ця ...
... . Істотним недоліком цього методу є неможливість сформулювати умови сумісності і визначеності системи залежно від значень коефіцієнтів і вільних членів. З іншого боку, навіть для визначеної системи цей метод не дає змоги знайти загальні формули, що визначають розв’язки системи через її коефіцієнти і вільні члени, які необхідно мати для теоретичних досліджень. Існують й інші методи розв’язування і ...
... чного сплайну. ; . Для знаходження коефіцієнті вкубічного сплайну призначена програма Work2_2. //------------------------------------------------------------ // Work2_2.cpp //------------------------------------------------------------ // "Числові методи" // Завдання 2 // Інтерполювання функції кубічним сплайном #include <stdio.h> #include <iostream.h> #include <conio ...
... (меньше 0,33%) одного з вільних членів системи (3) зовсім змінило розв’язок системи. На щастя, на практиці системи рівнянь, погано обумовлені, зустрічаються дуже рідко. 1.2 Методи розв’язування задачі Метод Жордана-Гаусса був розроблений двома вченими Жорданом та Гаусом (ві яких і пішла назва методу). Цей метод вони помітили після довгої практики роботи з системами рівнянь. Це можна ...
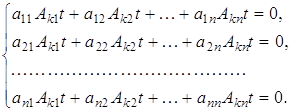
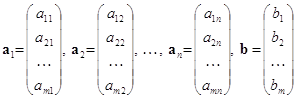
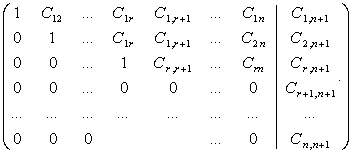
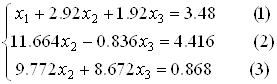
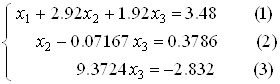
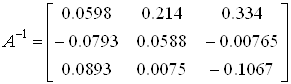
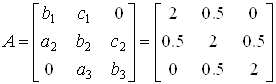
0 комментариев