Навигация
Розв’язання системи рівнянь методом Гауса
2.1 Розв’язання системи рівнянь методом Гауса
Приклад 1. Знайдемо розв’язок системи рівнянь методом Гауса:
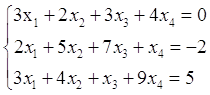
Сформуємо розширену матрицю:
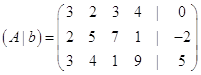
Прямий хід методу Гауса:
Крок 1.
Розділимо перший рядок матриці на ![]()
Отримаємо матрицю наступного вигляду:
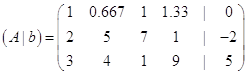
Крок 2.
Віднімаємо від другого рядка перший рядок, помножений на ![]()
Віднімаємо від третього рядка перший рядок, помножений на ![]()
Отримана модифікована матриця:
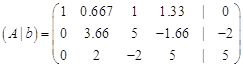
Крок 3.
Розділимо другий рядок на ![]() :
:
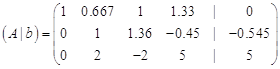
Крок 4.
Віднімаємо від третього рядка другий рядок, помножений на ![]()
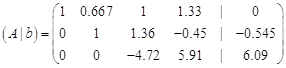
Крок 5.
Розділимо третій рядок матриці на ![]() :
:
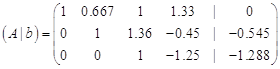
Прямий хід метода Гауса закінчено. Обернений хід метода Гауса. Утворюємо нулі вище головної діагоналі.
Крок 6.
Віднімаємо від другого рядка третій, помножений на ![]() Віднімаємо від першого рядка третій, помножений на
Віднімаємо від першого рядка третій, помножений на ![]() :
:
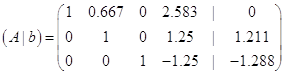
Крок 7.
Віднімаємо від першого рядка другий, помножений на ![]() :
:
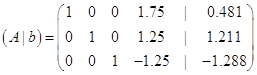
Запишемо систему рівнянь по останній розширеній матриці:
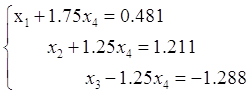
Змінні x1, x2, x3 залишемо в лівій частині рівняння, а х4 перенесимо вправо. Остаточний вигляд системи буде такий:
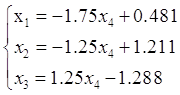
де х4 – вільна змінна.
Дана система рівнянь має безліч розв’язків.
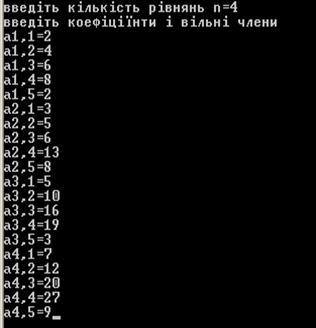
Приклад 2. Розв’яжемо СЛАР методом Гауса в MS Excel:
Цей метод розв'язання систем лінійних рівнянь придатний для розв'язання систем з будь-яким числом рівнянь і невідомих.
Запишемо нашу СЛАР в матричній формі:
![]()
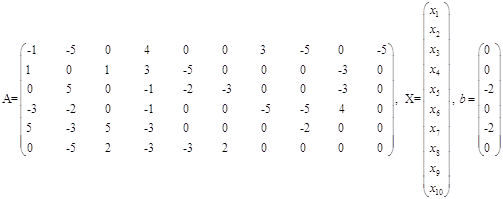
Отже маємо:
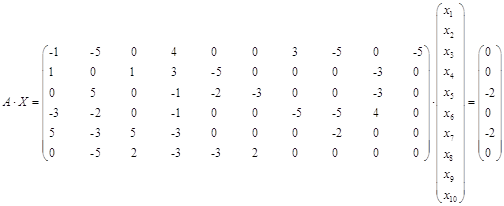
Помічений елемент матриці ![]() , оскільки він не дорівнює нулю отже виключаємо змінну
, оскільки він не дорівнює нулю отже виключаємо змінну ![]() і утворюємо нулі нижче
і утворюємо нулі нижче ![]() , отримуємо наступну матрицю:
, отримуємо наступну матрицю:
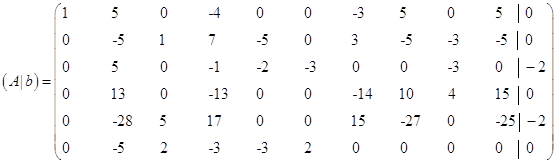
Якщо ж ![]() , то потрібно переставляти рядки. Вибираємо перший ненульовий елемент в стовпчику, що знаходиться нижче від розв’язувального елемента і переставляємо цей рядок на рядок з нульовим елементом
, то потрібно переставляти рядки. Вибираємо перший ненульовий елемент в стовпчику, що знаходиться нижче від розв’язувального елемента і переставляємо цей рядок на рядок з нульовим елементом ![]()
Аналогічно продовжуємо до отримання розв’язку СЛАР. В результаті отримаємо наступну табличку:
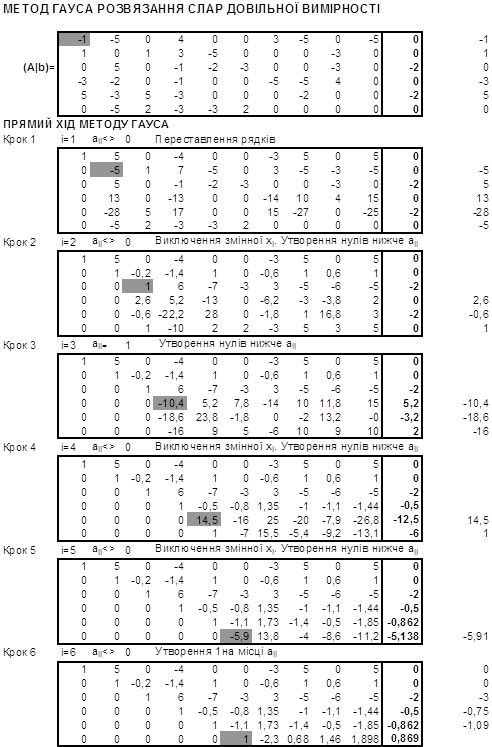
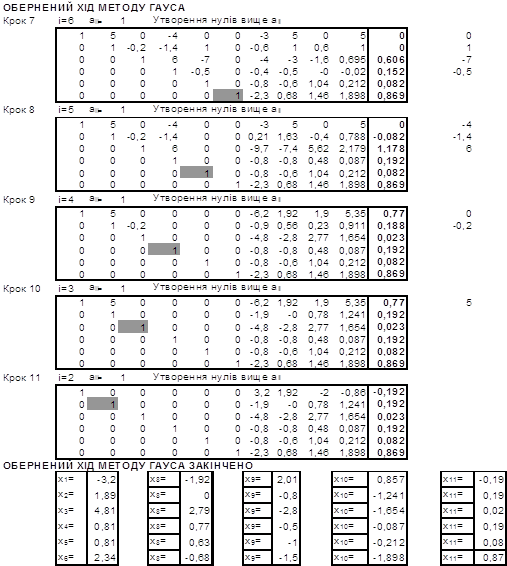
Отже в результаті отримали:
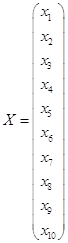 , де
, де ![]() - небазисні змінні.
- небазисні змінні.
Загальний розв’язок системи буде мати наступний вигляд:
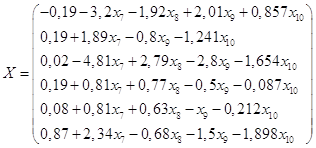 , де
, де ![]() - довільні.
- довільні.
Приклад 3. Розв’язання СЛАР з вибором головного елемента в MS Excel:
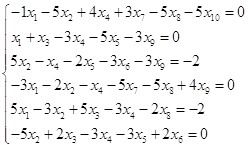
Суть даного методу полягає в тому, що на кожному кроці обирається напрямний рядок з максимальним абсолютним значенням розв’язувального елемента. Його перевагами у порівнянні з методом Гауса є те, що в результаті отримаємо меншу накопичену похибку за рахунок ділення напрямних рядків на більші елементи, але для погано обумовлених СЛАР похибка як і в методі Гауса може бути суттєвою.
Знаходження розв’язку за допомогою методу головного елемента описується наступним чином:
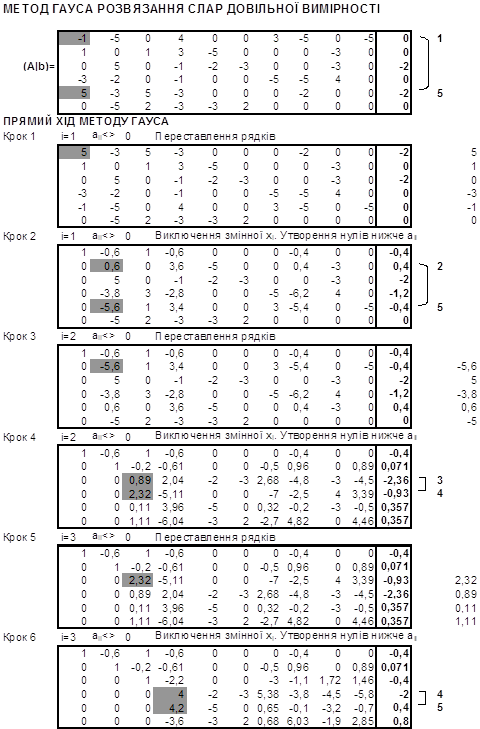

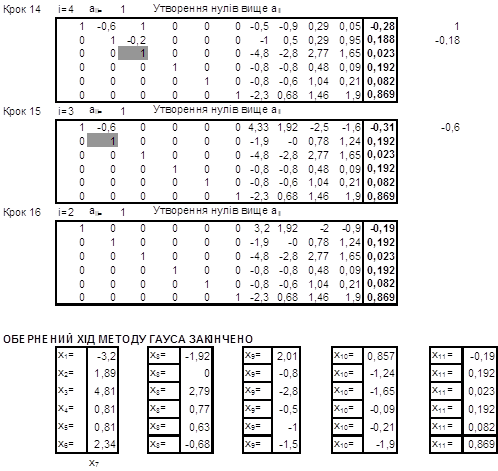
Загальний розв’язок системи має вигляд:
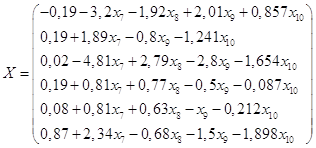 , де
, де ![]() - довільні.
- довільні.
Відповіді отриманні при розв’язуванні ідентичні, але кількість кроків виконаних, при реалізації метода головного елемента, дещо більша ніж в методі Гауса.
Похожие работы
... ’язок де С1, С2 - довільні сталі. Загальний розв’язок системи лінійних алгебраїчних рівнянь подається не в одному й тому самому вигляді. 2. Метод Гауса Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь полягає в послідовному виключенні змінних і перетворенні системи рівнянь (1) до трикутного вигляду (2) Припустимо, що в системі (1) коефіцієнт . Якщо ця ...
... . Істотним недоліком цього методу є неможливість сформулювати умови сумісності і визначеності системи залежно від значень коефіцієнтів і вільних членів. З іншого боку, навіть для визначеної системи цей метод не дає змоги знайти загальні формули, що визначають розв’язки системи через її коефіцієнти і вільні члени, які необхідно мати для теоретичних досліджень. Існують й інші методи розв’язування і ...
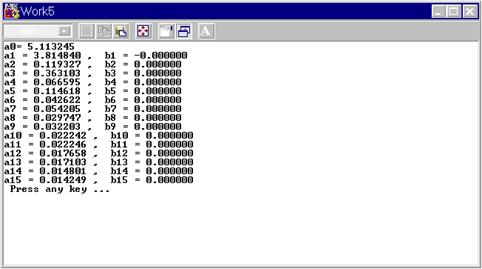
... чного сплайну. ; . Для знаходження коефіцієнті вкубічного сплайну призначена програма Work2_2. //------------------------------------------------------------ // Work2_2.cpp //------------------------------------------------------------ // "Числові методи" // Завдання 2 // Інтерполювання функції кубічним сплайном #include <stdio.h> #include <iostream.h> #include <conio ...
... (меньше 0,33%) одного з вільних членів системи (3) зовсім змінило розв’язок системи. На щастя, на практиці системи рівнянь, погано обумовлені, зустрічаються дуже рідко. 1.2 Методи розв’язування задачі Метод Жордана-Гаусса був розроблений двома вченими Жорданом та Гаусом (ві яких і пішла назва методу). Цей метод вони помітили після довгої практики роботи з системами рівнянь. Це можна ...
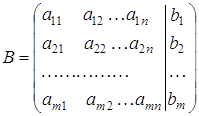
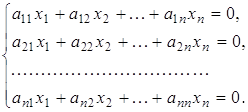
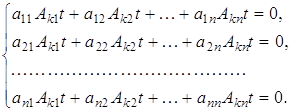
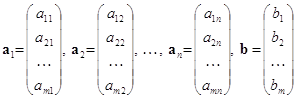

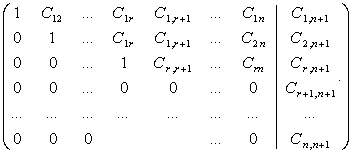
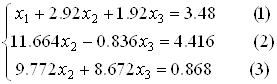
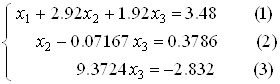
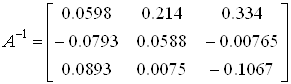
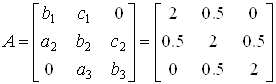
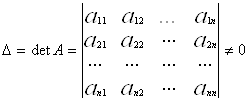
0 комментариев