Навигация
Обчислення рангу матриці
2.2 Обчислення рангу матриці
Приклад 4. Знайти ранг матриці:
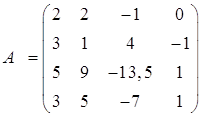
Розв’язання. Перший рядок залишаємо без змін. Щоб уникнути появи дробів, помножимо другу, третю та четверту рядки на 2:
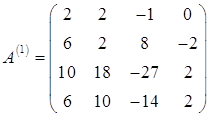
Перший рядок помножимо на ![]() і додамо до другого. Отримаємо рядок
і додамо до другого. Отримаємо рядок ![]() . Перший рядок помножимо на
. Перший рядок помножимо на ![]() і додамо до третього. Отримаємо рядок
і додамо до третього. Отримаємо рядок ![]() . Перший рядок помножимо на
. Перший рядок помножимо на ![]() і додамо до четвертого. Отримаємо рядок
і додамо до четвертого. Отримаємо рядок ![]() . У результаті маємо матрицю:
. У результаті маємо матрицю:
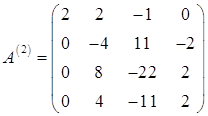
Другу рядок залишаємо без змін. На третьому рядку додаємо другий, помножений на 2. Отримаємо рядок ![]() . До четвертого рядка додаємо другий. Отримаємо нульовий рядок. Перетворена матриця має вигляд:
. До четвертого рядка додаємо другий. Отримаємо нульовий рядок. Перетворена матриця має вигляд:
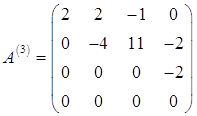
Поміняємо місцями третій і четвертий стовпчики:
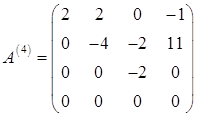
Базисний мінор матриці ![]() стоїть у перших трьох стовпцях і перших трьох рядках,
стоїть у перших трьох стовпцях і перших трьох рядках, ![]() . Отже,
. Отже, ![]() .
.
2.3 Опис та інструкція по використанню програми Gauss
Дана програма реалізована в інтегрованому середовищі програмування Visual Studio 2008 SP1 мовою програмування С#. Вона дозволяє розв’язувати систему лінійних алгебраїчних рівнянь методом Гауса, записаних в матричній формі, а також методом з пошуком головного елемента, при чому матриці можуть будь-якою вимірністю mxn (m і n – кількість стовпчиків та рядків матриці відповідно). Також ще однією з можливостей програми є обчислення рангу матриці.
Інтерфейс програми має наступний вигляд:

Мал. 1 Інтерфейс програми
Почати роботу з програмою користувач може двома способами:
· Вибрати запропоновані варіанти завдань
![]()
Мал. 2 Варіанти завдань
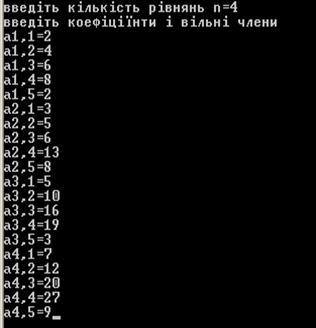
· Ввести вимірність матриці mxn у відповідних полях програми і натиснути кнопку «Застосувати»
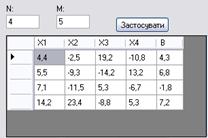
Мал. 3 Поле матриці mxn
Зауваження 1. Якщо ми маємо систему з чотирма рівняннями і чотирма невідомими, тобто матрицю А 4х4, то при введені даних в полях розмірності матриці, вважаємо, що B – це ще один стовпчик матриці А, яке це зображено на малюнку. 3.
Далі робота з програмою проходить наступним чином:
· В залежності від того яким методом ми хочемо розв’язати рівняння, натискаємо на кнопку «Метод Гауса», «метод головного елемента», що зображені на малюнку 4.
![]()
Мал. 4. Функціональні кнопки пошуку розв’язку
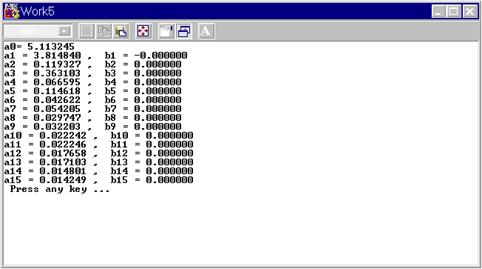
· Після натиснення на відповідну кнопку у вікну програми ми отримаємо загальний розв’язок системи, а також ранг матриці, що розглядаємо (малюнок 5)
· Далі у користувача буде декілька варіантів продовження роботи:
- Завершення роботи програми. Файл à Вихід, або закривши вікно програми, натиснувши на «хрестик».
- Збереження результатів програми у файл з послідовним описом кожного виконаного кроку (виключення змінної з розгляду та утворення нулів нижче-вище розв’язувального елемента; переставлення рядків)
- Знаходження розв’язку СЛАР при введених нових даних.
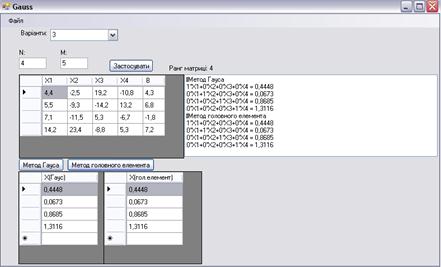
Мал. 5 Вікно програми після обчислень
Зауваження 2. Якщо вибране нами СЛАР розв’язку немає, то на екрані з’явиться повідомлення, в якому буде сказано, що методом Гауса розв’язку ми отримати не зможемо, а також буде вказано, який саме ранг буде мати дана матриця (малюнок 6).

Мал. 6 СЛАР розв’язків немає.
Перевіримо коректність роботи програмі на прикладі 6. (пункт 3.1)
Отримаємо розв’язок СЛАР, а також ранг матриці (малюнок 7)
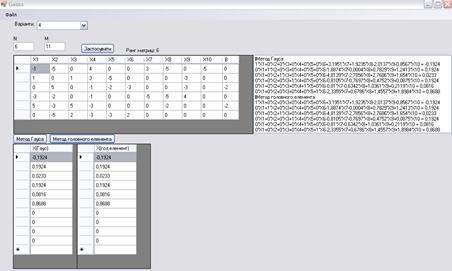
Мал. 7. Обчислення прикладу 6.
Збережемо детальний опис всіх кроків і відповідь у файл Excel з назвою Gauss.xls (малюнок 8). Якщо ж ми хочемо зберегти дані в блокноті, то тоді потрібно змінити розширення файлу на *.txt.
Мал. 8. Збереження результату.
Порівнявши дані результати з розв’язками, які ми отримали, при розв’язанні СЛАР за допомогою MS Excel, можемо стверджувати, що рівняння розв’язано правильно, оскільки відповіді ідентичні.

Опис основних функцій програми
Весь код програми знаходиться в додатках.
Розглянемо основні функції, які були задіяні при написанні програми:
Ø public void Gauss()- функція, яка безпосередньо відповідає за метод Гауса.
Ø public void Gauss2()- функція, яка відповідає за розв’язання методом головного елемента.
Ø public int Rang2()-функція знаходження рангу матриці.
Ø private void Flush(int i, int j)- функція, яка дозволяє переставляти рядки матриці.
Ø private int FindToFlush()- функція пошуку рядка, необхідного для переставлення по методу Гауса.
Ø private int FindToFlush2()- функцію пошуку рядка, необхідного для переставлення по методу головного елемента.
Ø private void ForwDirection(int i, int j)- функція, яка описує прямий хід методу Гауса.
Ø private void BackDirection(int i, int j) – обернений хід методу Гауса.
Ø private void MakeNull(int i)
private void MakeNullD- утворення нулів нижче розв’язувального елемента в прямому ході Гауса і утворення нулів вище розв’язувального елемента в обереному ході методу.
Список використаних джерел та літератури
1. Тарасов В.Н., Бахарева Н.Ф. Численные методы. Теория, алгоритмы, программы. – Оренбург: ИПК ОГУ, 2003.
2. Курош А.Г., “ Курс высшей алгебры ”, изд. 10, «Наука», Москва, 1971 г.
3. Овчинников П.Ф., Яремчук Ф.П., Михайленко В.М.. Высшая математика – К.: Вища шк. Главное изд., 1987 г.
4. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах.- М.: Наука
5. Г.Н.Воробьева, А.Н. Данилова. Практикум по вычислительной математике – Москва «Высшая школа», 1990.
6. Л.И.Турчак. Основы численных методов – Москва «Наука», 1987.
7. Фельдман Л.П., Петренко А.І., Дмитрієва О.А. Чисельні методи в інформатиці – Київ «Питер», 2006.
Похожие работы
... ’язок де С1, С2 - довільні сталі. Загальний розв’язок системи лінійних алгебраїчних рівнянь подається не в одному й тому самому вигляді. 2. Метод Гауса Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь полягає в послідовному виключенні змінних і перетворенні системи рівнянь (1) до трикутного вигляду (2) Припустимо, що в системі (1) коефіцієнт . Якщо ця ...
... . Істотним недоліком цього методу є неможливість сформулювати умови сумісності і визначеності системи залежно від значень коефіцієнтів і вільних членів. З іншого боку, навіть для визначеної системи цей метод не дає змоги знайти загальні формули, що визначають розв’язки системи через її коефіцієнти і вільні члени, які необхідно мати для теоретичних досліджень. Існують й інші методи розв’язування і ...
... чного сплайну. ; . Для знаходження коефіцієнті вкубічного сплайну призначена програма Work2_2. //------------------------------------------------------------ // Work2_2.cpp //------------------------------------------------------------ // "Числові методи" // Завдання 2 // Інтерполювання функції кубічним сплайном #include <stdio.h> #include <iostream.h> #include <conio ...
... (меньше 0,33%) одного з вільних членів системи (3) зовсім змінило розв’язок системи. На щастя, на практиці системи рівнянь, погано обумовлені, зустрічаються дуже рідко. 1.2 Методи розв’язування задачі Метод Жордана-Гаусса був розроблений двома вченими Жорданом та Гаусом (ві яких і пішла назва методу). Цей метод вони помітили після довгої практики роботи з системами рівнянь. Це можна ...
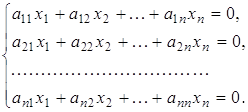

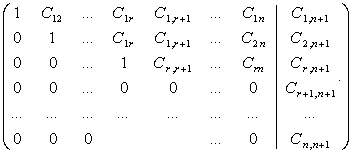
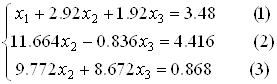
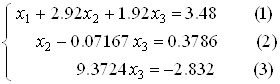
0 комментариев