Навигация
15 мин = 0,25 ч
1) 6 * 0,25 = 1,5 (км) – прошел поезд за 15 мин.
2) 7,5 + 1,5 = 9 (км) – прошел автобус до того, как догнал пешехода.
3) 9: 0,25 = 36 (км/ч) – скорость автобуса.
Ответ: 36 км/ч.
Задача 2: (№ 1169)
«а) Теплоход идет вниз по реке. Какова скорость движения теплохода, если скорость течения реки 4 км/ч, а собственная скорость теплохода (скорость в стоячей воде) равна 21 км/ч?
б) Моторная лодка идет вверх по реке. Какова скорость движения лодки, если скорость течения 3 км/ч, а собственная скорость лодки 14 км/ч?»
| Собств. v | V течения | V по течению реки | V против течения |
| 21 | 4 | ? | - |
| 14 | 3 | - | ? |
а) 21 + 4 = 25 (км/ч) – скорость теплохода.
б) 14 – 3 = 11 (км/ч) – скорость движения лодки.
Ответ: а) 25 км/ч;
б) 11 км/ч.
Задача 3: (№ 1172)
«Со станции вышел товарный поезд со скоростью 50 км/ч. Через 3 ч. с той же станции вслед за ним вышел электропоезд со скоростью 80 км/ч. Через сколько часов после своего выхода электропоезд догонит товарный поезд?
![]()
![]()
![]()
![]()
![]()
![]() 80 км/ч 50 км/ч
80 км/ч 50 км/ч
![]()
![]()
![]()
3 ч. tвстр - ?
1) 50 ∙ 3 = 150 (км) – прошел товарный поезд.
2) 80 – 50 = 30 (км/ч) – скорость сближения.
3) 150 : 30 = 5 (ч) – через это время электропоезд догонит товарный поезд.
Ответ: через 5 часов.
Задача 4: (№ 1179)
«Два поезда вышли в разное время навстречу друг другу из двух городов, расстояние между которыми 782 км. Скорость первого поезда 52 км/ч, а второго 61 км/ч. Пройдя 416 км, первый поезд встретился со вторым. На сколько один из поездов вышел раньше другого?»
![]()
![]()
![]()
![]() 52 км/ч 61 км/ч
52 км/ч 61 км/ч

416 км
782 км
1) 416: 52 = 8 (ч) – шел первый поезд.
2) 782 – 416 = 366 (км) – прошел второй поезд.
3) 366: 6 = 6 (ч) – шел второй поезд.
4) 8 – 6 = 2 (ч) – на это время первый поезд вышел раньше второго.
Ответ: на 2 часа.
Задача 5: (№ 1193)
«Собственная скорость катера (скорость в стоячей воде) равна 21,6 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость катера по течению и против течения реки.»
| Собств. v | V течения | V по течению реки | V против течения |
| 21,6 | 4,7 | ? | ? |
1) 21,6 + 4,7 = 26,3 (км/ч) – скорость катера по течению.
2) 21,6 – 4,7 = 16,9 (км/ч) – скорость катера против течения.
Ответ: 26,3 км/ч; 16,9 км/ч.
Задача 6: (№ 1194)
«Скорость теплохода по течению реки равна 37,6 км/ч. Найдите собственную скорость теплохода и его скорость против течения, если скорость течения реки 3,9 км/ч.»
| Собств. v | V течения | V по течению реки | V против течения |
| ? | 3,9 | 37,6 | ? |
1) 37,6 – 3,9 = 33,7 (км/ч) – собственная скорость теплохода.
2) 33,7 – 3,9 = 29,8 (км/ч) – скорость против течения.
Ответ: 33, 7 км/ч; 29,8 км/ч.
Задача 7: (№ 1196)
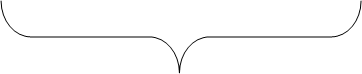
«Расстояние между городами 156 км. Из них одновременно навстречу друг другу выехали два велосипедиста. Один проезжает в час 13,6 км, а другой 10,4 км. Через сколько часов они встретятся?»
![]()
![]()
![]()
![]()
![]() 13,6 км/ч 10,4 км/ч
13,6 км/ч 10,4 км/ч
![]()
![]()
![]()
![]()
1 ч. tвстр -?. 1 ч.
156 км
1) 13,6 + 10,4 = 24 (км/ч) – скорость сближения.
2) 156: 24 = 6,5 (ч) – через это время они встретятся.
Ответ: через 6,5 часа.
Задача 8: (№ 1233)
«Автомашина в первый час прошла 48,3 км, во второй час она прошла на 15,8 км меньше, чем в первый, а в третий час – на 24,3 км меньше, чем за первые два часа вместе. Какой путь прошла автомашина за эти три часа?»
![]()
![]() 1 ч.
1 ч.
48,3 км
![]()
![]()
![]()
![]()
![]() 2 ч. ?
2 ч. ?
? 15,8 км
![]()
![]()
![]()
![]()
![]() 3 ч.
3 ч.
? 24,3 км
1) 48,3 – 15,8 = 32,5 (км) – прошла машина за 2-ой час.
2) 48,3 + 32,5 = 80,8 (км) – прошла машина за 1 и 2 час.
3) 80,8 – 24,3 = 56,5 (км) – прошла машина за 3-ий час.
4) 56,5 + 80,8 = 137,3 (км) – прошла машина за 3 часа.
Ответ: 137,3 км.
Задача 9: (№ 1268)
«Собственная скорость лодки 4,5 км/ч, скорость течения 2,5 км/ч. Найдите скорость лодки при движении по течению и против течения. Какой путь пройдет лодка по течению за 4 часа, и какой путь она пройдет против течения за 3 часа?»
| Собств. v | V течения | t (ч) | S (км) | |
| по течению реки | 4,5 | 2,5 | 4 | ? |
| против течения | 4,5 | 2,5 | 3 | ? |
1) 4,5 + 2,5 = 7 (км/ч) – скорость по течению.
2) 4,5 – 2,5 = 2 (км/ч) – скорость против течения.
3) 7 ∙ 4 = 28 (км) – путь по течению реки.
4) 2 ∙ 3 = 6 (км) – путь против течения реки.
Ответ: 28 км; 6км.
Задача 10: (№ 1285)
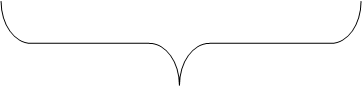
«Автомашина прошла 3 ч со скоростью 48,4 км/ч и 5 ч со скоростью 56,6 км/ч. Какой путь прошла автомашина за все это время?»
![]()
![]()
![]()
![]() 48,4 км/ч 56,6 км/ч
48,4 км/ч 56,6 км/ч
![]()
![]()
![]()
Похожие работы
... , таблица). Метод моделирования позволяет активизировать познавательную деятельность учащихся на уроке. 2.2. Опытно – экспериментальная работа. Анализ ее результатов Изучив теоретические положения по использованию моделирования при решении задач в 5 классе, у автора возникло желание и интерес реализовать это на практике. Для того чтобы доказать или опровергнуть предположение, что ...
... , заполняя клетки таблицы, школьники должы обратить внимание на совпадение парных сумм, например: 35+47=45+37=82. А + В А В 43 45 47 49 33 35 37 39 2.2. Обучение решению задач на движение с помощью схематического моделирования На подготовительном этапе на ...
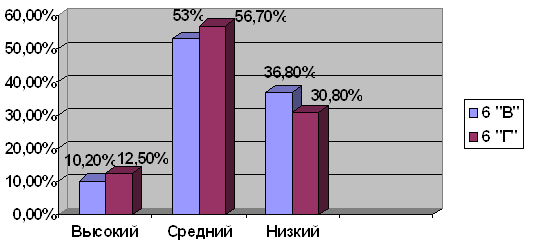
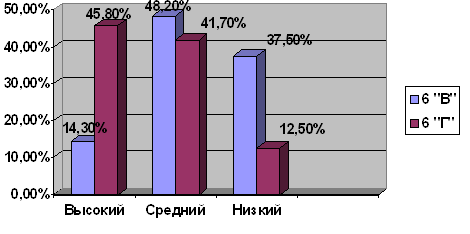
... и перенести полученные знания на практику. Глава 2. Работа учителя по развитию логического мышления на уроках математики 2.1 Опытно-экспериментальная работа и анализ ее результатов Опытно-экспериментальное исследование по выявлению уровня развития логического мышления школьников при решении текстовых задач проводилось на базе МОУ «Средняя общеобразовательная школа № 10» г. Кунгура в ...
... быть усовершенствована путем внедрения в процесс обучения учебных моделей, эвристические возможности которых шире, чем у обычной наглядности. Глав 2.Применение моделирования при изучении орфографии в начальной школе 2.1.Орфографическая работа в начальной школе О чем обычно в первую очередь заботится учитель, начиная вводить первоклассников в проблемы орфографии? О том, ...

0 комментариев