Навигация
Точка, прямая и плоскость в пространстве. Векторы
64015
знаков
3
таблицы
8
изображений
1.1 Точка, прямая и плоскость в пространстве. Векторы
Понятие точка является определяющим понятием пространства, любая фигура пространства состоит из множества точек. Хранение в памяти компьютера информации о элементах пространства будем осуществлять с помощью хранения координат точек определяющих данный элемент пространства. Так для хранения информации о прямой достаточно всего двух различных точек принадлежащих этой прямой. По двум точкам задающим прямую можно составить каноническое уравнение прямой и далее оперировать этим уравнением:
, (1′)
где точки 
и 
принадлежат данной прямой. Или если использовать вектор 
т.е. 
, получим следующее уравнение прямой:
. (1′′)
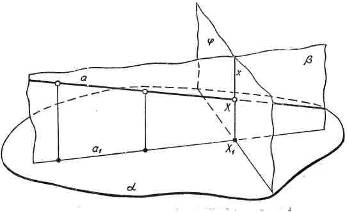
Аналогично прямой, плоскость определяется тремя точками:
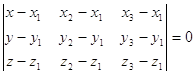, (2′)
где точки , , 
принадлежат данной плоскости из этой матрицы можно получить уравнение плоскости:
, (2′′)
где коэффициенты 
,
,
,
определяются следующим способом:
;
;
;
.
Причем из этих формул полезно знать, что координатами вектора нормального к данной плоскости являются соответственно коэффициенты ,,. Этот вектор направлен в полупространство правого обхода точек.
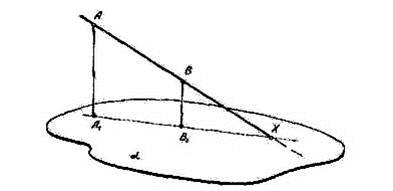
Решая совместно уравнения (1′′) и (2′′) найдем координаты точки пересечения прямой и плоскости, при условии, что прямая пересекает плоскость. Пусть плоскость задана тремя точками: , , , а прямая задана двумя точками: 
и 
, тогда координаты точки пересечения 
находятся по формулам:
,
где 
, причем если 
, то 
; (1x)
,
где 
, причем если 
, то 
; (1y)
,
где 
, причем если 
, то 
. (1z)
В этих формулах координаты вектора для прямой вычисляется следующим образом: 
.
Похожие работы
... встречи прямой (рёбер многогранника) с секущей плоскостью. (http://www.ssau.ru/books/gubanov/lection1.htm) Основной типовой задачей на эту тему в школьной программе является построение сечения, по трем, заданным на поверхности многогранника, точкам, принадлежащим секущей плоскости. Алгоритм построения такого сечения следующий: 1) Выбираем наиболее подходящую грань многогранника для ...
... задачи. Решение задач на построение сечений Работа по ознакомлению учащихся с проекционным чертежом может быть продолжена при обучении решению задач на построение сечений многогранников. Обучение решению задач на построение сечений можно проводить в следующем плане. Во-первых, первоначальное ознакомление учащихся с методами построения сечений следует проводить на метрически определенных ...
... подобраны опорные задачи, которые можно использовать на уроке при изучении данной темы. Таким образом, в данной работе были рассмотрены основные, общие моменты изучения многогранников в школьном курсе стереометрии. В следствие чего дальнейшие исследования могут проходить в направлении более детального изучения отдельных разделов данной темы, а также пропедевтического введения многогранников в ...
... имеют достаточно четкое и правильное представление из собственного жизненного опыта, а формулировки которых являются слишком громоздкими. Выводы по § 1 1. Основные цели изучения темы «Объемы многогранников» в курсе стереометрии – развитие пространственных представлений учащихся, освоение способов вычисления практически важных величин и дальнейшее развитие логического мышления учащихся. ...
0 комментариев