Навигация
Преобразования пространства
1.2 Преобразования пространства
Для реализации интерактивности изучения пространственных тел необходимо реализовать возможность перемещения, поворота и масштабирования, а для этого необходимо изменять координаты точек фигур по соответствующему закону. Рассмотрим три преобразования которые переводят каждую точку ![]() в точку
в точку ![]() :
:
1. Перемещение (параллельный перенос на вектор ![]() ).
).
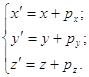 (1p)
(1p)
2. Поворот вокруг прямой на угол ![]() . Поворот будем осуществлять вокруг одной из осей координат.
. Поворот будем осуществлять вокруг одной из осей координат.
а) вокруг оси OX:
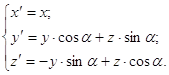 (2px)
(2px)
б) вокруг оси OY:
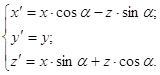 (2py)
(2py)
в) вокруг оси OZ:
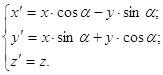 (2pz)
(2pz)
3. Масштабирование с коэффициентом ![]() .
.
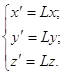 (3p)
(3p)
1.3 Пространственные тела
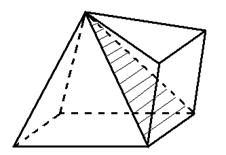
Как уже говорилось, в памяти компьютера пространственные тела будем хранить в виде координат точек определяющих эти тела. Рассмотрим далее, как хранить те или иные виды пространственных тел и рассмотрим основные способы создания фигур. При описании многогранников необходимо задание координат всех вершин многогранников, а также описание порядка обхода каждой грани. Удобно описывать обход граней почасовой стрелке наблюдая многогранник из вне, тогда нормальный вектор к грани, заданный тройкой следующих подряд вершин, будет направлен из многогранника. Это свойство удобно использовать при визуализации выпуклых многогранников, об этом будет рассказано позднее. С многогранниками все понятно, а как описывать поверхности второго порядка (поверхности вращения, конические поверхности, цилиндрические поверхности, эллипсоид, гиперболоид, параболоид). Их можно представить в виде многогранника с большим количеством граней, и чем больше количество граней, тем точнее приближение. Этот метод является универсальным, он позволяет описывать комбинированные пространственные тела, но не позволяет изучать алгебраические кривые, которые получаются при построении сечений. Приведем общую структуру файла, описывающего многогранник. Файл представляет собой обычный текстовый документ.
Количество вершин многогранника.
Координаты 1й вершины через пробел.
Координаты 2й вершины через пробел.
Количество граней многогранника.
Порядок обхода 1й грани через пробел.
Порядок обхода 2й грани через пробел.
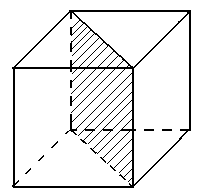
Пример описания куба с ребром равным 2.
| 8 0 0 2 2 0 2 2 2 2 0 2 2 0 0 0 2 0 0 2 2 0 0 2 0 6 1 5 8 4 2 3 7 6 5 6 7 8 4 3 2 1 3 4 8 7 2 6 5 1 | |
1.4 Поверхности второго порядка
| № | Название. | Способ описания. |
| 1. | Конус | Как пирамида с большим числом вершин, в основании которой лежит правильный многоугольник. |
| 2. | Цилиндр | Как призма с большим числом вершин, основаниями которой являются правильные многоугольники. |
| 3. | Сфера | Многогранник, описанный по принципу параллелей и меридианов. |
| 4. | Тор | Совокупность косоугольных цилиндров. |
Пример1: Методов получения координат точек сферы.
| for iy:=0 to ny-1 do for ix:=0 to nx do begin x:=r*sin(iy*pi/ny)*cos(2*ix*pi/nx); y:=r*sin(iy*pi/ny)*sin(2*ix*pi/nx); z:=r*cos(iy*pi/ny); x:=r*sin((iy+1)*pi/ny)*cos(2*ix*pi/nx); y:=r*sin((iy+1)*pi/ny)*sin(2*ix*pi/nx); z:=r*cos((iy+1)*pi/ny); end; |
|
Глава II. Изучение сечений пространственных тел
Похожие работы
... встречи прямой (рёбер многогранника) с секущей плоскостью. (http://www.ssau.ru/books/gubanov/lection1.htm) Основной типовой задачей на эту тему в школьной программе является построение сечения, по трем, заданным на поверхности многогранника, точкам, принадлежащим секущей плоскости. Алгоритм построения такого сечения следующий: 1) Выбираем наиболее подходящую грань многогранника для ...
... задачи. Решение задач на построение сечений Работа по ознакомлению учащихся с проекционным чертежом может быть продолжена при обучении решению задач на построение сечений многогранников. Обучение решению задач на построение сечений можно проводить в следующем плане. Во-первых, первоначальное ознакомление учащихся с методами построения сечений следует проводить на метрически определенных ...
... подобраны опорные задачи, которые можно использовать на уроке при изучении данной темы. Таким образом, в данной работе были рассмотрены основные, общие моменты изучения многогранников в школьном курсе стереометрии. В следствие чего дальнейшие исследования могут проходить в направлении более детального изучения отдельных разделов данной темы, а также пропедевтического введения многогранников в ...
... имеют достаточно четкое и правильное представление из собственного жизненного опыта, а формулировки которых являются слишком громоздкими. Выводы по § 1 1. Основные цели изучения темы «Объемы многогранников» в курсе стереометрии – развитие пространственных представлений учащихся, освоение способов вычисления практически важных величин и дальнейшее развитие логического мышления учащихся. ...



0 комментариев