Навигация
Методы построения сечений многогранников
2.1 Методы построения сечений многогранников
Геометрические задачи традиционно делятся на три типа:
1) на вычисление;
2) на доказательство;
3) на построение.
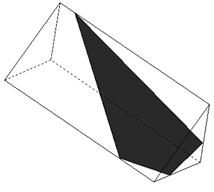
Решение любых стереометрических задач требует не только вычислительных и логических умений и навыков, но и умений изображать пространственные фигуры на плоскости (например, на листе бумаги, классной доске), что по сути своей тесно связано с темой «Геометрические построения на плоскости». Стереометрические задачи на вычисления и доказательство легко можно решать, используя правильный рисунок пространственной фигуры. При изучении тем «Параллельность прямых и плоскостей в пространстве», «Перпендикулярность прямых и плоскостей», «Углы между прямой и плоскостью, между двумя прямыми, между двумя плоскостями» и других тем прекрасным иллюстрационным материалом является решение позиционных и метрических задач на построение пространственных фигур и сечений этих фигур плоскостями. Основными методами построения сечений многогранников являются следующие методы:
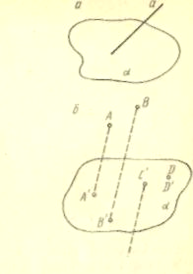
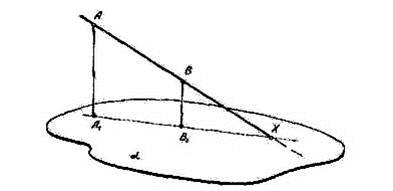
1. Метод следов. Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры. Последовательно соединяя образы этих точек, получим изображение искомого сечения.
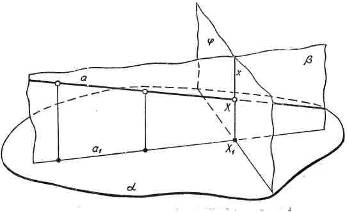
2. Метод вспомогательных сечений. Этот метод построения сечений многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь в виду, что построения, выполняемые при использовании этого метода, зачастую получаются «скученными». Тем не менее, в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.
3. Комбинированный метод построения сечений. Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с методом следов и методом вспомогательных сечений.
4. Координатный метод построения сечений. Суть координатного метода заключается в вычислении координат точек пересечения ребер или многогранника с секущей плоскостью, которая задается уравнением плоскости. Уравнение плоскости сечения вычисляется на основе условий задачи.
Из всех перечисленных способов построения сечения наиболее приемлемым является координатный метод, так как он связан с большим объемом вычислений и имеет простой алгоритм реализации, что целесообразно реализовать с помощью ЭВМ. Достаточно знать координаты вершин каждой грани многогранника и три точки задающие плоскость сечения.
2.2 Задание сечений пространственных тел
Как уже говорилось, удобнее всего задавать плоскость сечения тремя точками, причем координаты этих точек должны быть известны или должны вычисляться. Рассмотрим возможные варианты задания точек плоскости сечения:
1) точка расположена вне многогранника;
2) точка находится внутри многогранника;
3) точка расположена в грани многогранника;
4) точка принадлежит ребру многогранника;
5) точка принадлежит диагонали многогранника;
6) точка совпадает с вершиной многогранника.
Условие задания секущей плоскости тремя точками будет выполняться не всегда и в этом случае придется вычислять уравнение плоскости сечения, используя другие методы. В данной работе рассматривается лишь способ задания тремя точками.
2.3 Построение сечений пространственных тел. Алгоритм
Метод построения сечения заключается в нахождении точек пересечения секущей плоскости с гранями многогранника, а вернее с ребрами многогранника. Проверка на пересечение секущей плоскости и ребра многогранника производится следующим образом:
1. Составление уравнения секущей плоскости по трем точкам;
2. Подстановка в уравнение координат концов ребра с целью проверки: расположены ли точки в разных полупространствах относительно плоскости сечения.
3. Нахождение точки пересечения ребра многогранника и плоскости сечения.
Для каждой грани записываются две точки, причем запись производится только для тех граней, где плоскость сечения пересекла два ребра. Далее используя полученные данные, строится многоугольник сечения следующим образом:
1. Берем первую пару точек и ищем следующую пару точек в которой повторяется одна из точек первой пары.
2. Найдя следующую пару проделываем для нее тоже самое, что и для первой пары, но исключаем из поиска первую пару.
3. Проделываем весь алгоритм для каждой пары, пока не останется одна ненайденная точка.
4. Полученная цепочка является последовательным описанием ребер многоугольника сечения.
Далее запоминаем полученный многоугольник, как новую грань многогранника.
2.4 Исследование свойств сечения
Перечислим некоторые свойства сечения (исходя из факта, что сечением является многоугольник).
1. Уравнение плоскости сечения.
2. Количество вершин многоугольника сечения.
3. Площадь многоугольника сечения.
4. Координаты вершин многоугольника сечения.
5. Двугранный угол между плоскостью сечения и гранями многогранника.
6. Углы при вершинах многоугольника сечения.
Некоторые из этих свойств реализованы в программе (1,2,3,4).
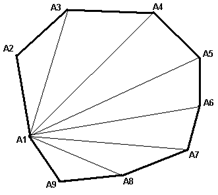
Пример: Нахождение площади сечения. Так как строятся сечения выпуклых многогранников, то многоугольник сечения будет тоже выпуклым, т.е. его площадь можно найти разбиением на треугольники (площадь сечения равна сумме площадей треугольников из которых оно составлено).
Глава III. Визуализация
Похожие работы
... встречи прямой (рёбер многогранника) с секущей плоскостью. (http://www.ssau.ru/books/gubanov/lection1.htm) Основной типовой задачей на эту тему в школьной программе является построение сечения, по трем, заданным на поверхности многогранника, точкам, принадлежащим секущей плоскости. Алгоритм построения такого сечения следующий: 1) Выбираем наиболее подходящую грань многогранника для ...
... задачи. Решение задач на построение сечений Работа по ознакомлению учащихся с проекционным чертежом может быть продолжена при обучении решению задач на построение сечений многогранников. Обучение решению задач на построение сечений можно проводить в следующем плане. Во-первых, первоначальное ознакомление учащихся с методами построения сечений следует проводить на метрически определенных ...
... подобраны опорные задачи, которые можно использовать на уроке при изучении данной темы. Таким образом, в данной работе были рассмотрены основные, общие моменты изучения многогранников в школьном курсе стереометрии. В следствие чего дальнейшие исследования могут проходить в направлении более детального изучения отдельных разделов данной темы, а также пропедевтического введения многогранников в ...
... имеют достаточно четкое и правильное представление из собственного жизненного опыта, а формулировки которых являются слишком громоздкими. Выводы по § 1 1. Основные цели изучения темы «Объемы многогранников» в курсе стереометрии – развитие пространственных представлений учащихся, освоение способов вычисления практически важных величин и дальнейшее развитие логического мышления учащихся. ...


0 комментариев